Bước 1: Tìm độ dài các cạnh \(AB, BC, CD, DA, AC, BD. . . \) Bước 2. Phân tích, đưa ra lời giải Giải bài 4 trang 91 sách bài tập toán 10 – Chân trời sáng tạo – Bài 1. Khái niệm vectơ. Cho hình thoi ABCD cạnh bằng a và có tâm O…
Đề bài/câu hỏi:
Cho hình thoi ABCD cạnh bằng a và có tâm O, góc \(\widehat {BAD} = 60^\circ \)
a) Tìm trong hình hai vectơ bằng nhau, và có độ dài bằng \(\frac{{a\sqrt 3 }}{2}\)
b) Tìm trong hai hình đối nhau và có độ dài bằng \(a\sqrt 3 \)
Hướng dẫn:
Bước 1: Tìm độ dài các cạnh \(AB,BC,CD,DA,AC,BD…\)
Bước 2: Xác định hướng của các vectơ có độ dài bằng \(\frac{{a\sqrt 3 }}{2};a\sqrt 3 \)
Bước 3: a) Từ bước 2, chỉ ra hai vectơ cùng hướng
b) Từ bước 2, chỉ ra hai vectơ ngược hướng
Lời giải:
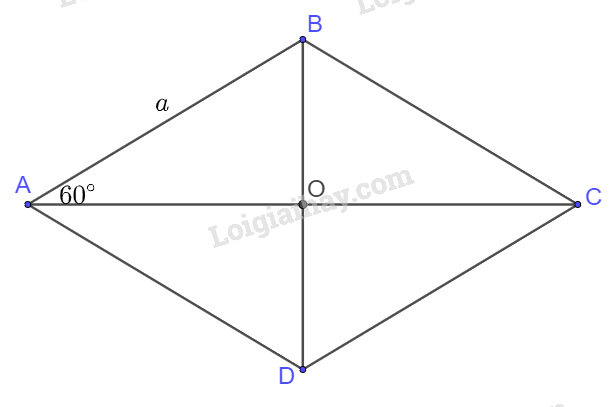
a) \(AB = BC = CD = DA = a\)
Mặt khác \(\widehat {BAD} = 60^\circ \), suy ra tam giác ABD đều, suy ra \(BD = a,AO = \frac{{a\sqrt 3 }}{2}\)
\( \Rightarrow BD = 2DO = OB = a;AC = 2AO = 2CO = a\sqrt 3 \)
Suy ra các cặp vectơ bằng nhau và có độ dài bằng \(\frac{{a\sqrt 3 }}{2}\) là:
\(\overrightarrow {AO} \)và \(\overrightarrow {OC} \); \(\overrightarrow {CO} \) và \(\overrightarrow {OA} \)
b) Các cặp vectơ đối nhau và có độ dài bằng \(a\sqrt 3 \)là: \(\overrightarrow {AC} \)và \(\overrightarrow {CA} \)