Giải chi tiết Giải bài 4 trang 75 sách bài tập toán 10 – Chân trời sáng tạo – Bài 2. Định lí côsin và định lí sin. Tính khoảng cách giữa hai điểm P và Q của một hồ nước (hình 7)….
Đề bài/câu hỏi:
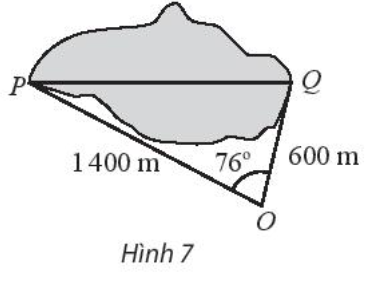
Tính khoảng cách giữa hai điểm P và Q của một hồ nước (hình 7). Cho biết từ một điểm O cách hai điểm P và Q lần lượt là 1400 m và 600 m người quan sát nhìn thấy một góc \(76^\circ \)
Lời giải:
Áp dụng định lí côsin ta có:
\(\begin{array}{l}P{C^2} = O{P^2} + O{Q^2} – 2OP.OQ.\cos O\\ = {1400^2} + {600^2} – 2.1400.600.\cos 76^\circ = 1913571,215\\ \Rightarrow PQ = \sqrt {1913571,215} \simeq 1383,32\end{array}\)
Vậy khoảng cách giữa hai điểm P và Q của hồ nước trên gần bằng 1383,32 m