Hướng dẫn giải Giải bài 10 trang 102 sách bài tập toán 10 – Chân trời sáng tạo – Bài tập cuối Chương 5. Cho tam giác ABC vuông tại A. KHẳng định nào sau đây là sai?…
Đề bài/câu hỏi:
Cho tam giác ABC vuông tại A. KHẳng định nào sau đây là sai?
A. \(\overrightarrow {AB} .\overrightarrow {AC} < \overrightarrow {BA} .\overrightarrow {BC} \)
B. \(\overrightarrow {AC} .\overrightarrow {CB} < \overrightarrow {AC} .\overrightarrow {BC} \)
C. \(\overrightarrow {AB} .\overrightarrow {BC} < \overrightarrow {CA} .\overrightarrow {CB} \)
D. \(\overrightarrow {AC} .\overrightarrow {BC} < \overrightarrow {BC} .\overrightarrow {AB} \)
Lời giải:
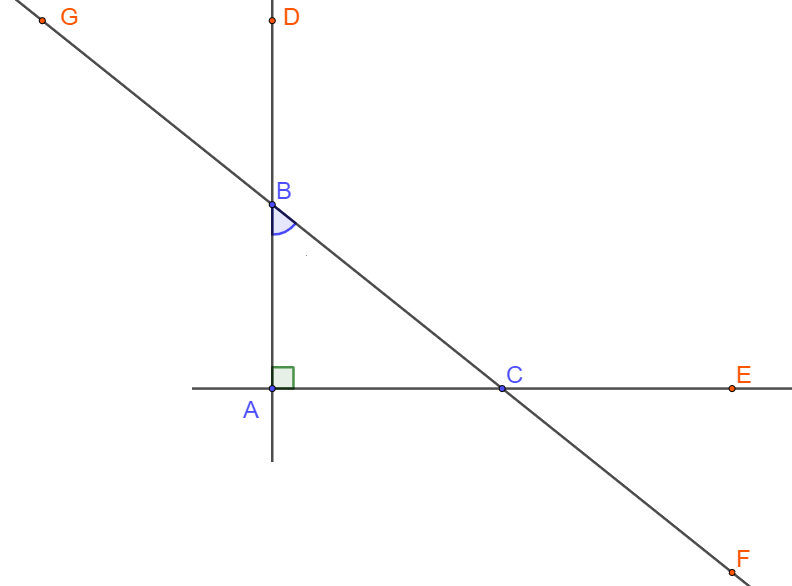
A. \(\overrightarrow {AB} .\overrightarrow {AC} < \overrightarrow {BA} .\overrightarrow {BC} \)
+ \(\overrightarrow {AB} .\overrightarrow {AC} = 0\)
+ \(\cos \left( {\overrightarrow {BA} ,\overrightarrow {BC} } \right) = \cos B > 0\) (vì \({0^ \circ } < \widehat B < {90^ \circ }\))
\( \Rightarrow \overrightarrow {BA} .\overrightarrow {BC} > 0 = \overrightarrow {AB} .\overrightarrow {AC} \)=> A đúng
B. \(\overrightarrow {AC} .\overrightarrow {CB} < \overrightarrow {AC} .\overrightarrow {BC} \)
+ \(\cos \left( {\overrightarrow {AC} ,\overrightarrow {CB} } \right) = \cos \left( {\overrightarrow {CE} ,\overrightarrow {CB} } \right) = \cos \widehat {BCE} {90^ \circ }\))
+ \(\cos \left( {\overrightarrow {AC} ,\overrightarrow {BC} } \right) = \cos \left( {\overrightarrow {CE} ,\overrightarrow {CF} } \right) = \cos \widehat {ECF} > 0\) (vì \({0^ \circ } < \widehat C < {90^ \circ }\))
\( \Rightarrow \overrightarrow {AC} .\overrightarrow {CB} < 0 B đúng
C. \(\overrightarrow {AB} .\overrightarrow {BC} < \overrightarrow {CA} .\overrightarrow {CB} \)
+ \(\cos \left( {\overrightarrow {AB} ,\overrightarrow {BC} } \right) = \cos \left( {\overrightarrow {BD} ,\overrightarrow {BC} } \right) = \cos \widehat {CBD} {90^ \circ }\))
+ \(\cos \left( {\overrightarrow {CA} ,\overrightarrow {CB} } \right) = \cos \widehat C > 0\) (vì \({0^ \circ } < \widehat C < {90^ \circ }\))
\( \Rightarrow \overrightarrow {AB} .\overrightarrow {BC} < 0 C đúng
D. \(\overrightarrow {AC} .\overrightarrow {BC} < \overrightarrow {BC} .\overrightarrow {AB} \)
+ \(\cos \left( {\overrightarrow {AC} ,\overrightarrow {BC} } \right) = \cos \left( {\overrightarrow {CE} ,\overrightarrow {CF} } \right) = \cos \widehat {ECF} > 0\) (vì \({0^ \circ } < \widehat {ECF} < {90^ \circ }\))
+ \(\cos \left( {\overrightarrow {BC} ,\overrightarrow {AB} } \right) = \cos \left( {\overrightarrow {BC} ,\overrightarrow {BD} } \right) = \cos \widehat {CBD} {90^ \circ }\))
\( \Rightarrow \overrightarrow {AC} .\overrightarrow {BC} > 0 > \overrightarrow {BC} .\overrightarrow {AB} \) => D đúng
Chọn D.