Bài 1 trang 65 SBT toán 10 – Chân trời sáng tạo: Tìm các giá trị của tham số a, b, c để phương trình ax + by + c = 0

Đề bài/câu hỏi:

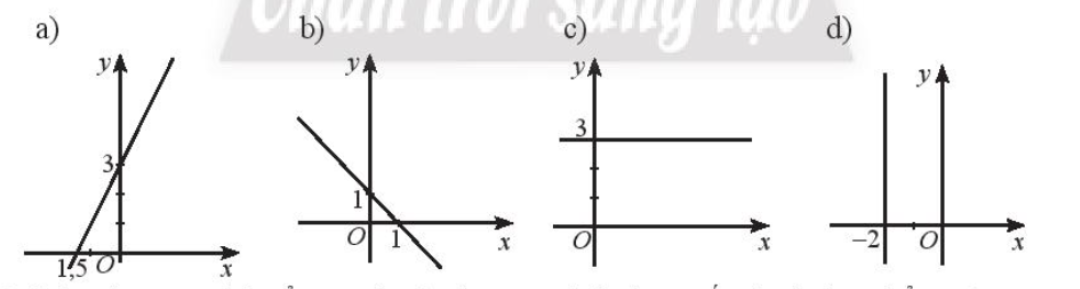
Tìm các giá trị của tham số a, b, c để phương trình \(ax + by + c = 0\) có thể biểu diễn được các đường thẳng trong hình dưới đây

Hướng dẫn:

Đường thẳng \(d:ax + by + c = 0\), điểm \(A\left( {{a_0},{b_0}} \right)\) thuộc đường thẳng d khi \(a{a_0} + b{b_0} + c = 0\)

Lời giải:

a) \(\left\{ \begin{array}{l}\left( {0;3} \right) \in d\\\left( { – 1,5;0} \right) \in d\end{array} \right. \Rightarrow \left\{ \begin{array}{l}a.0 + b.3 + c = 0\\a\left( { – 1,5} \right) + b.0 + c = 0\end{array} \right. \Rightarrow \left\{ \begin{array}{l}3b + c = 0\\\left( { – 1,5} \right)a + c = 0\end{array} \right.\)

Chọn \(c = 3 \Rightarrow a = 2,b = – 1\)

Phương trình đường thẳng là \(2x – y + 3 = 0\)

b) \(\left\{ \begin{array}{l}\left( {0;1} \right) \in d\\\left( {1;0} \right) \in d\end{array} \right. \Rightarrow \left\{ \begin{array}{l}a.0 + b.1 + c = 0\\a.1 + b.0 + c = 0\end{array} \right. \Rightarrow \left\{ \begin{array}{l}b + c = 0\\a + c = 0\end{array} \right.\)

Cho \(c = – 1 \Rightarrow a = 1,b = 1\)

Phương trình đường thẳng là \(x + y – 1 = 0\)

c) \(\left\{ \begin{array}{l}\left( {0;3} \right) \in d\\\left( {1;3} \right) \in d\end{array} \right. \Rightarrow \left\{ \begin{array}{l}a.0 + b.3 + c = 0\\a.1 + b.3 + c = 0\end{array} \right. \Rightarrow \left\{ \begin{array}{l}3b + c = 0\\a + 3b + c = 0\end{array} \right.\)

Cho \(c = – 3 \Rightarrow a = 0,b = 1\)

Phương trình đường thẳng là \(y – 3 = 0\)

d) \(\left\{ \begin{array}{l}\left( { – 2;1} \right) \in d\\\left( { – 2;0} \right) \in d\end{array} \right. \Rightarrow \left\{ \begin{array}{l}a.\left( { – 2} \right) + b.1 + c = 0\\a\left( { – 2} \right) + b.0 + c = 0\end{array} \right. \Rightarrow \left\{ \begin{array}{l} – 2a + b + c = 0\\ – 2a + c = 0\end{array} \right.\)

Cho \(c = 2 \Rightarrow a = 1,b = 0\)

Phương trình đường thẳng là \(x + 2 = 0\)