Sử dụng tính chất đường trung tuyến trong tam giác và xác định hướng các vectơ tương ứng. Lời giải Giải bài 48 trang 99 SBT toán 10 – Cánh diều – Bài 5. Tích của một số với một vectơ. Cho tam giác ABC và M là trung điểm của BC, G là trọng tâm của tam giác….
Đề bài/câu hỏi:
Cho tam giác ABC và M là trung điểm của BC, G là trọng tâm của tam giác. Khẳng định nào sau đây đúng?
A. \(\overrightarrow {AM} = – 3\overrightarrow {GM} \)
B. \(\overrightarrow {AM} = \frac{3}{2}\overrightarrow {GM} \)
C. \(\overrightarrow {AM} = – \frac{3}{2}\overrightarrow {GM} \)
D. \(\overrightarrow {AM} = 3\overrightarrow {GM} \)
Hướng dẫn:
Sử dụng tính chất đường trung tuyến trong tam giác và xác định hướng các vectơ tương ứng
Lời giải:
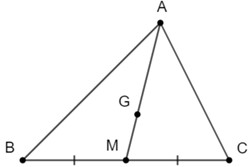
∆ABC có AM là đường trung tuyến và G là trọng tâm nên \(AG = \frac{2}{3}AM\) \( \Rightarrow AM = 3GM\)
Lại có G nằm giữa A và M \( \Rightarrow \overrightarrow {AM} = 3\overrightarrow {GM} \)
Chọn D