Bài 44 trang 61 SBT toán 10 – Cánh diều: Người ta muốn thiết kế một vườn hoa hình chữ nhật nội tiếp trong một miếng đất hình tròn có đường kính bằng 50 m (Hình 23)

Đề bài/câu hỏi:

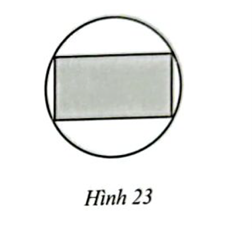
Người ta muốn thiết kế một vườn hoa hình chữ nhật nội tiếp trong một miếng đất hình tròn có đường kính bằng 50 m (Hình 23). Xác định kích thước vườn hoa hình chữ nhật để tổng quãng đường đi xung quanh vườn hoa đó là 140 m.

Hướng dẫn:

Đặt độ dài 1 cạnh của hình chữ nhật là \(x\)(m) (\(0 < x < 50\)).

Biểu diễn cạnh còn lại và chu vi của hình chữ nhật theo x.

Lời giải:

Đặt độ dài một cạnh của hình chữ nhật là \(x\)(m) (\(0 < x < 50\)).

Độ dài đường chéo hình chữ nhật = Đường kính đường tròn = 50m.

Độ dài cạnh còn lại của hình chữ nhật đó là \(\sqrt {{{50}^2} – {x^2}} = \sqrt {2500 – {x^2}} \) (m)

Khi đó, tổng quãng đường đi xung quanh vườn hoa bằng chu vi hình chữ nhật là: \(2\left( {\sqrt {2500 – {x^2}} + x} \right) = 140\) (m)

Ta có phương trình: \(2\left( {\sqrt {2500 – {x^2}} + x} \right) = 140 \Leftrightarrow \sqrt {2500 – {x^2}} + x = 70 \Rightarrow \sqrt {2500 – {x^2}} = 70 – x\)

\(\begin{array}{l} \Leftrightarrow \left\{ \begin{array}{l}x > 0\\70 – x \ge 0\\2500 – {x^2} = {\left( {70 – x} \right)^2}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}0 < x \le 70\\2500 – {x^2} = {x^2} – 140x + {70^2}\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}0 < x \le 70\\2{x^2} – 140x + 2400 = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}0 < x \le 70\\\left[ \begin{array}{l}x = 30\\x = 40\;\end{array} \right.\quad \end{array} \right.\end{array}\)

Nếu \(x = 40\) thì độ dài cạnh còn lại là 30 (m) và ngược lại.

Vậy kích thước vườn hoa là 30 x 40 (m)