Bước 1: Sử dụng tính chất O là trung điểm AC. Lời giải Giải bài 43 trang 92 SBT toán 10 – Cánh diều – Bài 4. Tổng và hiệu của hai vectơ. Cho tứ giác ABCD là hình bình hành. Gọi O là giao điểm của hai đường chéo ,…
Đề bài/câu hỏi:
Cho tứ giác ABCD là hình bình hành. Gọi O là giao điểm của hai đường chéo , E là trung điểm của AD, G là giao điểm của BE và AC. Tính:
a) \(\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} + \overrightarrow {OD} \)
b) \(\overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GD} \)
Hướng dẫn:
Bước 1: Sử dụng tính chất O là trung điểm AC, BD để tính \(\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} + \overrightarrow {OD} \)
Bước 2: Chứng minh G là trọng tâm tam giác ABD rồi tính \(\overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GD} \)
Lời giải:
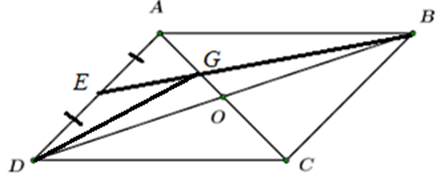
a) Do ABCD là hình bình hành nên O là trung điểm AC và BD
\( \Rightarrow \overrightarrow {OA} + \overrightarrow {OC} = \overrightarrow 0 ,\overrightarrow {OB} + \overrightarrow {OD} = \overrightarrow 0 \) \(\begin{array}{l} \Rightarrow \overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} + \overrightarrow {OD} = \left( {\overrightarrow {OA} + \overrightarrow {OC} } \right) + \left( {\overrightarrow {OB} + \overrightarrow {OD} } \right)\\ = \overrightarrow 0 + \overrightarrow 0 = \overrightarrow 0 \end{array}\)
b) Xét tam giác ABD có AO và BE là hai đường trung tuyến cắt nhau tại G
\( \Rightarrow \) G là trọng tâm ∆ABD \( \Rightarrow \overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GD} = \overrightarrow 0 \)