Bài 39 trang 92 SBT toán 10 – Cánh diều: Cho tam giác đều ABC cạnh a. Tính: a) | → AB + → BC | b) | → AB – → AC |

Đề bài/câu hỏi:

Cho tam giác đều ABC cạnh a. Tính:

a) \(\left| {\overrightarrow {AB} + \overrightarrow {BC} } \right|\)

b) \(\left| {\overrightarrow {AB} – \overrightarrow {AC} } \right|\)

c) \(\left| {\overrightarrow {AB} + \overrightarrow {AC} } \right|\)

Hướng dẫn:

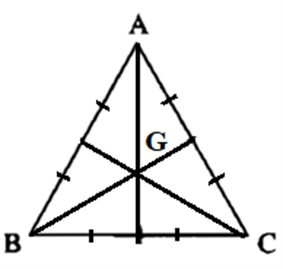
Bước 1: Lấy G là trọng tâm tam giác ABC

Bước 2: Sử dụng quy tắc cộng, quy tắc trừ, quy tắc 3 điểm (lấy G là điểm trung gian) để biến đổi và tính độ dài các vectơ tương ứng

Lời giải:

Gọi G là trọng tâm tam giác ABC

Khi đó \(\overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} = \overrightarrow 0 \), \(GA = GB = GC = \frac{{a\sqrt 3 }}{3}\)

a) Ta có: \(\left| {\overrightarrow {AB} + \overrightarrow {BC} } \right| = \left| {\overrightarrow {AC} } \right| = AC = a\)

b) Ta có: \(\left| {\overrightarrow {AB} – \overrightarrow {AC} } \right| = \left| {\overrightarrow {CB} } \right| = BC = a\)

c) Ta có: \(\left| {\overrightarrow {AB} + \overrightarrow {AC} } \right| = \left| {\left( {\overrightarrow {GB} – \overrightarrow {GA} } \right) + \left( {\overrightarrow {GC} – \overrightarrow {GA} } \right)} \right| = \left| {\left( {\overrightarrow {GB} + \overrightarrow {GC} } \right) – 2\overrightarrow {GA} } \right|\) (1)

Lại có: \(\overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} = \overrightarrow 0 \Leftrightarrow \overrightarrow {GB} + \overrightarrow {GC} = – \overrightarrow {GA} \) (2)

Từ (1) và (2) suy ra \(\left| {\overrightarrow {AB} + \overrightarrow {AC} } \right| = \left| { – \overrightarrow {GA} – 2\overrightarrow {GA} } \right| = \left| { – 3\overrightarrow {GA} } \right| = 3\left| {\overrightarrow {GA} } \right| = 3GA = 3.\frac{{a\sqrt 3 }}{3} = a\sqrt 3 \)