Cho tam thức bậc hai \(f\left( x \right) = a{x^2} + bx + c\left( {a \ne 0} \right), \Delta = {b^2} – 4ac\. Gợi ý giải Giải bài 23 trang 52 SBT toán 10 – Cánh diều – Bài 3. Dấu của tam thức bậc hai. Lập bảng xét dấu mỗi tam thức bậc hai sau:…
Đề bài/câu hỏi:
Lập bảng xét dấu mỗi tam thức bậc hai sau:
a) \(f\left( x \right) = 3{x^2} – 7x + 4\)
b) \(f\left( x \right) = 25{x^2} + 10x + 1\)
c) \(f\left( x \right) = 3{x^2} – 2x + 8\)
d) \(f\left( x \right) = – 2{x^2} + x + 3\)
e) \(f\left( x \right) = – 3{x^2} + 6x – 3\)
g) \(f\left( x \right) = – 5{x^2} + 2x – 4\)
Hướng dẫn:
Cho tam thức bậc hai \(f\left( x \right) = a{x^2} + bx + c\left( {a \ne 0} \right),\Delta = {b^2} – 4ac\)
+ Nếu \(\Delta < 0\) thì \(f\left( x \right)\) cùng dấu với hệ số \(a\) với mọi \(x \in \mathbb{R}\)
+ Nếu \(\Delta = 0\) thì \(f\left( x \right)\) cùng dấu với hệ số \(a\) với mọi \(x \in \mathbb{R}\backslash \left\{ {\frac{{ – b}}{{2a}}} \right\}\)
+ Nếu \(\Delta > 0\) thì \(f\left( x \right)\) có hai nghiệm \({x_1},{x_2}\left( {{x_1} < {x_2}} \right)\). Khi đó:

Lời giải:
a) \(f\left( x \right) = 3{x^2} – 7x + 4\) có hai nghiệm \({x_1} = 1;{x_2} = \frac{4}{3}\) và có hệ số \(a = 3 > 0\)
Ta có bảng xét dấu của \(f\left( x \right)\) như sau:
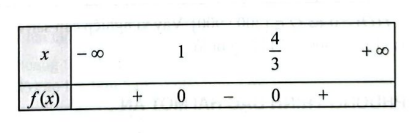
b) \(f\left( x \right) = 25{x^2} + 10x + 1\) có nghiệm kép \({x_0} = \frac{{ – 1}}{5}\) và có hệ số \(a = 25 > 0\)
Ta có bảng xét dấu của \(f\left( x \right)\) như sau:
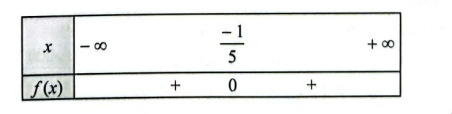
c) \(f\left( x \right) = 3{x^2} – 2x + 8\) vô nghiệm và có hệ số \(a = 3 > 0\)
Ta có bảng xét dấu của \(f\left( x \right)\) như sau:
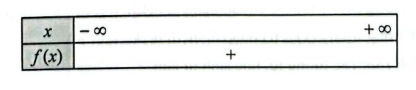
d) \(f\left( x \right) = – 2{x^2} + x + 3\) có hai nghiệm \({x_1} = – 1;{x_2} = \frac{3}{2}\) và có hệ số \(a = – 2 < 0\)
Ta có bảng xét dấu của \(f\left( x \right)\) như sau:
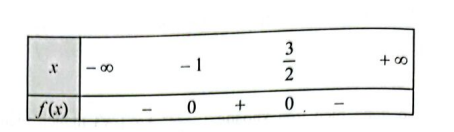
e) \(f\left( x \right) = – 3{x^2} + 6x – 3\) có nghiệm kép \({x_0} = 1\) và có hệ số \(a = – 3 < 0\)
Ta có bảng xét dấu của \(f\left( x \right)\) như sau:

g) \(f\left( x \right) = – 5{x^2} + 2x – 4\) vô nghiệm và có hệ số \(a = – 5 < 0\)
Ta có bảng xét dấu của \(f\left( x \right)\) như sau:
