Trả lời Giải đề 2 Tổng hợp 10 đề thi học kì 1 Toán 10 kết nối tri thức – Đề thi đề kiểm tra Toán lớp 10 Kết nối tri thức.
Câu hỏi/Đề bài:
HƯỚNG DẪN GIẢI CHI TIẾT
I. Trắc nghiệm (7 điểm)
|
1. B |
6. C |
11. D |
16. A |
21. A |
26. B |
31. D |
|
2.A |
7. D |
12. C |
17. B |
22. C |
27. B |
32. A |
|
3. A |
8. C |
13. D |
18. D |
23. D |
28. B |
33. C |
|
4. A |
9. D |
14. D |
19. C |
24. A |
29. D |
34. A |
|
5. B |
10. D |
15. D |
20. D |
25. D |
30. C |
35. D |
Câu 1 (NB):
Hướng dẫn:
Mệnh đề là câu khẳng định, có tính đúng hoặc sai.
Cách giải:
(1) và (4) là mệnh đề.
Chọn B.
Câu 2 (TH):
Hướng dẫn:
Phủ định của \(\forall \) là \(\exists \), phủ định của > là \( \le \).
Cách giải:
Mệnh đề phủ định của mệnh đề “\(\forall x \in \mathbb{R},{\kern 1pt} {\kern 1pt} x – 2 > 5\)” là “\(\exists x \in \mathbb{R},{\kern 1pt} {\kern 1pt} x – 2 \le 5\)”.
Chọn A.
Câu 3 (TH):
Hướng dẫn:
Viết tập hợp theo cách liệt kê các phần tử.
Cách giải:
Giải phương trình \(x\left( {x – 2} \right)\left( {x – 3} \right) = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{x = 0}\\{x = 2}\\{x = 3}\end{array}} \right.\).
Mà \(x \in {\mathbb{N}^*} \Rightarrow x \in \left\{ {2;3} \right\}.\)
Vậy D = {2;3}.
Chọn A.
Câu 4 (TH):
Hướng dẫn:
Chỉ ra các tính chất đặc trưng cho các phần tử của tập hợp B và viết tập hợp B theo cách nêu tính chất đặc trưng cho các phần tử của tập hợp.
Cách giải:
B = {3;6;9;12;15}
\( \Rightarrow B = \left\{ {3n|n \in \mathbb{N},{\kern 1pt} {\kern 1pt} 1 \le n \le 5} \right\}\).
Chọn A.
Câu 5 (VD):
Hướng dẫn:
Thực hiện các phép toán trên tập hợp. Sử dụng trục số.
Cách giải:
+) \(A \cap B = \left( { – 3; – 2} \right]\)
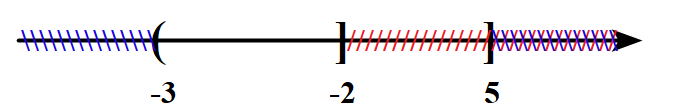
=> A đúng.
+) \(A\backslash B = \left( { – \infty ; – 3} \right]\)

=> B sai.
+) \(A \cup B = \left( { – \infty ;5} \right]\)

=> C đúng.
+) \(B\backslash A = \left( { – 2;5} \right]\).
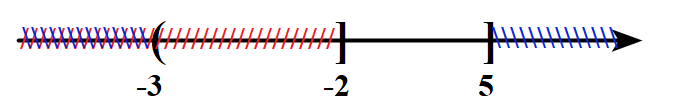
=> D đúng.
Chọn B.
Câu 6 (NB):
Hướng dẫn:
Tập hợp A được gọi là tập con của tập hợp B nếu mọi phần tử của tập hợp A đều là phần tử của tập hợp B.
Cách giải:
\({A_3} = \left\{ {4;5} \right\} \subset A = \left\{ {1;2;3;4;5} \right\}\).
Chọn C.
Câu 7 (NB):
Hướng dẫn:
Tìm khẳng định đúng.
Cách giải:
5 là số nguyên tố, 9, 12, 4 là hợp số nên mệnh đề D đúng.
Chọn D.
Câu 8 (TH):
Hướng dẫn:
Bất phương trình bậc nhất hai ẩn x, y có dạng tổng quát là
\(ax + by \le c\) (\(ax + by \ge c\), \(ax + by c\))
Trong đó a, b, c là những số thực đã cho, a và b không đồng thời bằng 0, x và y là các ẩn số.
Cách giải:
Ta có: \(2{x^2} + 1 \ge y + 2{x^2} \Leftrightarrow y – 1 \le 0\) nên đây là một bất phương trình bậc nhất hai ẩn.
Chọn C.
Câu 9 (NB):
Hướng dẫn:
Thay các tọa độ điểm vào bất phương trình, điểm nào thỏa mãn bất phương trình thì thuộc miền nghiệm của bất phương trình đó.
Cách giải:
+) Thay tọa độ điểm (5;1) vào bất phương trình ta có: 3.5 + 2.1 (5;1) không thuộc miền nghiệm của bất phương trình.
+) Thay tọa độ điểm (4;2) vào bất phương trình ta có: 3.4 + 2.2 (4;2) không thuộc miền nghiệm của bất phương trình.
+) Thay tọa độ điểm (1;5) vào bất phương trình ta có: 3.1 + 2.5 (1;5) không thuộc miền nghiệm của bất phương trình.
+) Thay tọa độ điểm (1;2) vào bất phương trình ta có: 3.1 + 2.2 (1;2) không thuộc miền nghiệm của bất phương trình.
Chọn D.
Câu 10 (NB):
Hướng dẫn:
Sử dụng định lí cosin trong tam giác: \({a^2} = {b^2} + {c^2} – 2bc.\cos A.\)
Cách giải:
\(E{F^2} = E{G^2} + F{G^2} – 2EG.FG.\cos G\) là mệnh đề đúng.
Chọn D.
Câu 11 (TH):
Hướng dẫn:
Áp dụng định lí Sin trong tam giác ABC: \(\frac{{AC}}{{\sin B}} = \frac{{AB}}{{\sin C}} \Rightarrow \frac{{\sin B}}{{\sin C}} = \frac{{AC}}{{AB}}\).
Cách giải:
Áp dụng định lí Sin trong tam giác ABC ta có: \(\frac{{AC}}{{\sin B}} = \frac{{AB}}{{\sin C}} \Rightarrow \frac{{\sin B}}{{\sin C}} = \frac{{AC}}{{AB}}\).
Theo giả thiết \(\frac{{\sin B}}{{\sin C}} = \sqrt 3 \Rightarrow \frac{{AC}}{{AB}} = \sqrt 3 \Rightarrow AC = \sqrt 3 AB.\)
Vậy \(AC = \sqrt 3 .2\sqrt 2 = 2\sqrt 6 .\)
Chọn D.
Câu 12 (VD):
Hướng dẫn:
Tính sinA.
Tính diện tích tam giác ABC: \(S = \frac{1}{2}bc.\sin A.\)
Sử dụng định lí cosin trong tam giác tính a: \({a^2} = {b^2} + {c^2} – 2bc.\cos A.\)
Sử dụng công thức tính diện tích tam giác: \(S = \frac{1}{2}a{h_a}\), từ đó tính \({h_a}\).
Cách giải:
Ta có:
\(\begin{array}{*{20}{l}}{{{\sin }^2}A + {{\cos }^2}A = 1}\\{ \Leftrightarrow {{\sin }^2}A + {{\left( {\frac{3}{5}} \right)}^2} = 1}\\{ \Leftrightarrow {{\sin }^2}A = \frac{{16}}{{25}}}\end{array}\)
Vì \({0^0} < A 0 \( \Rightarrow \sin A = \frac{4}{5}.\)
Diện tích tam giác ABC là: \(S = \frac{1}{2}bc.\sin A. = \frac{1}{2}.7.5.\frac{4}{5} = 14.\)
Áp dụng định lí cosin trong tam giác ABC ta có:
\(\begin{array}{*{20}{l}}{{a^2} = {b^2} + {c^2} – 2bc.\cos A.}\\{{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} = {7^2} + {5^2} – 2.7.5.\frac{3}{5}}\\{{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} = 32}\\{ \Rightarrow a = 4\sqrt 2 .}\end{array}\)
Lại có: \(S = \frac{1}{2}a{h_a} \Rightarrow {h_a} = \frac{{2S}}{a} = \frac{{2.14}}{{4\sqrt 2 }} = \frac{{7\sqrt 2 }}{2}.\)
Chọn C.
Câu 13 (TH):
Hướng dẫn:
Với x là nghiệm của phương trình đã cho thì mệnh đề P(x) là mệnh đề đúng.
Cách giải:
Ta có: \({x^2} – 5x + 4 = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{x = 1}\\{x = 4}\end{array}} \right.\).
Vậy với x = 1 thì P(x) là mệnh đề đúng.
Chọn D.
Câu 14 (NB):
Hướng dẫn:
Hệ bất phương trình bậc nhất hai ẩn là một hệ gồm hai hay nhiều bất phương trình bậc nhất hai ẩn.
Cách giải:
\(\left\{ {\begin{array}{*{20}{l}}{x – 4 \ge y}\\{3x + 4y < 5}\end{array}} \right.\) là hệ bất phương trình bậc nhất hai ẩn.
Chọn D.
Câu 15 (NB):
Hướng dẫn:
Nhớ bảng giá trị lượng giác của các góc thường dùng hoặc sử dụng máy tính cầm tay.
Cách giải:
\(\begin{array}{*{20}{l}}{T = 2 + {{\sin }^2}{{90}^0} + 2{{\cos }^2}{{60}^0} – 3{{\tan }^2}{{45}^0}}\\{T = 2 + {1^2} + 2.{{\left( {\frac{1}{2}} \right)}^2} – {{3.1}^2}}\\{T = \frac{1}{2}.}\end{array}\)
Chọn D.
Câu 16 (NB):
Hướng dẫn:
Sử dụng các công thức tính diện tích tam giác: \({S_{ABC}} = \frac{1}{2}ab\sin C = pr = \frac{{abc}}{{4S}} = \frac{1}{2}c.{h_c}.\)
Cách giải:
\({S_{ABC}} = \frac{1}{2}ab\sin C\) nên đáp án A sai.
Chọn A.
Câu 17 (NB):
Hướng dẫn:
Áp dụng định lí Cosin trong tam giác: \(A{B^2} = B{C^2} + A{C^2} – 2BC.AC.\cos C\).
Cách giải:
Áp dụng định lí Cosin trong tam giác ABC:
\(\begin{array}{*{20}{l}}{A{B^2} = B{C^2} + A{C^2} – 2BC.AC.\cos C}\\{{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} = {1^2} + {3^2} – 2.1.3.\cos {{60}^0} = 7}\\{ \Rightarrow AB = \sqrt 7 .}\end{array}\)
Chọn B.
Câu 18 (NB):
Hướng dẫn:
Mệnh đề đảo của mệnh đề \(P \Rightarrow Q\) là \(Q \Rightarrow P\).
Cách giải:
Mệnh đề đảo của mệnh đề “Nếu tứ giác là một hình thoi thì tứ giác đó nội tiếp được một đường tròn” là
Chọn D.
Câu 19 (NB):
Hướng dẫn:
Biểu diễn tập hợp trên trục số.
Cách giải:
Hình vẽ đã cho là minh họa cho tập hợp \(\left[ {1; + \infty } \right).\)
Chọn C.
Câu 20 (NB):
Hướng dẫn:
Sử dụng mối liên hệ giá trị lượng giác của hai góc bù nhau: Cho \(\alpha \) và \(\beta \) là hai góc khác nhau và bù nhau ta có: \(\sin \alpha = \sin \beta ,\) \(\cos \alpha = – \cos \beta \), \(\tan \alpha = – \tan \beta \), \(\cot \alpha = – \cot \beta .\)
Cách giải:
\(\alpha \) và \(\beta \) là hai góc khác nhau và bù nhau nên \(\sin \alpha = \sin \beta ,\) \(\cos \alpha = – \cos \beta \), \(\tan \alpha = – \tan \beta \), \(\cot \alpha = – \cot \beta .\)
Vậy đẳng thức ở đáp án D sai.
Chọn D.
Câu 21 (TH):
Hướng dẫn:
\({C_B}A = B\backslash A = \{ x|x \in B\) và \(x \notin A\)}.
Cách giải:
Ta có: \({C_B}A = B\backslash A = \{ x|x \in B\) và \(x \notin A\)}.
\( \Rightarrow {C_B}A = \left\{ {3;5;7;8} \right\}.\)
Chọn A.
Câu 21 (VD):
Hướng dẫn:
Sử dụng hệ quả định lí cosin trong tam giác ABC tính cosB: \(\cos B = \frac{{A{B^2} + B{C^2} – A{C^2}}}{{2AB.BC}}\).
Tính BM, CM.
Sử dụng định lí cosin trong tam giác ABM tính AM: \(A{M^2} = A{B^2} + B{M^2} – 2AB.BM.\cos B\).
Cách giải:
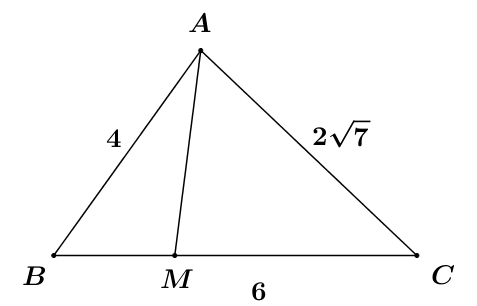
Ta có:
\(\begin{array}{*{20}{l}}{\cos B = \frac{{A{B^2} + B{C^2} – A{C^2}}}{{2AB.BC}}}\\{{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} = \frac{{{4^2} + {6^2} – {{\left( {2\sqrt 7 } \right)}^2}}}{{2.4.6}} = \frac{1}{2}}\end{array}\)
Vì MC = 2MB, BC = 6 nên \(BM = \frac{1}{3}BC = \frac{1}{3}.6 = 2.\)
Áp dụng định lí cosin trong tam giác ABM ta có:
\(\begin{array}{*{20}{l}}{A{M^2} = A{B^2} + B{M^2} – 2AB.BM.\cos B}\\{{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} = {4^2} + {2^2} – 2.4.2.\frac{1}{2} = 12}\\{ \Rightarrow AM = 2\sqrt 3 .}\end{array}\)
Chọn C.
Câu 23 (TH):
Hướng dẫn:
Tìm phương trình đường thẳng d. Loại đáp án.
Thay tọa độ điểm O(0;0) vào các bất phương trình chưa bị loại ở các đáp án, tiếp tục loại đáp án.
Cách giải:
Đường thẳng d đi qua điểm (0;1) nên loại đáp án B, C.
Ta thấy điểm O(0;0) không thuộc miền nghiệm của bất phương trình.
+ Thay tọa độ điểm O(0;0) vào bất phương trình \(2x + y < 1\) ta có: 2.0 + 0 Loại.
+ Thay tọa độ điểm O(0;0) vào bất phương trình \(2x + y > 1\) ta có: 2.0 + 0 > 1 (Vô lí) => Thỏa mãn.
Chọn D.
Câu 24 (TH):
Hướng dẫn:
Sử dụng công thức: \(1 + {\tan ^2}\alpha = \frac{1}{{{{\cos }^2}\alpha }}.\)
Cách giải:
Ta có:
\(\begin{array}{*{20}{l}}{{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} 1 + {{\tan }^2}\alpha = \frac{1}{{{{\cos }^2}\alpha }}}\\{ \Leftrightarrow 1 + {{\left( { – 2\sqrt 2 } \right)}^2} = \frac{1}{{{{\cos }^2}\alpha }}}\\{ \Leftrightarrow {{\cos }^2}\alpha = \frac{1}{9}}\\{ \Leftrightarrow \cos \alpha = \pm \frac{1}{3}}\end{array}\)
Vì \({0^0} < \alpha 0\). Mà \(\tan \alpha = \frac{{\sin \alpha }}{{\cos \alpha }} < 0\) nên \(\cos \alpha < 0\).
Vậy \(\cos \alpha = – \frac{1}{3}.\)
Chọn A.
Câu 25 (VD):
Hướng dẫn:
Hướng N300E là hướng tạo với hướng bắc một góc 300 và tạo với hướng đông một góc \({90^0} – {30^0} = {60^0}\).
Áp dụng định lí cosin trong tam giác.
Cách giải:
Hướng N300E là hướng tạo với hướng bắc một góc 300 và tạo với hướng đông một góc \({90^0} – {30^0} = {60^0}\).
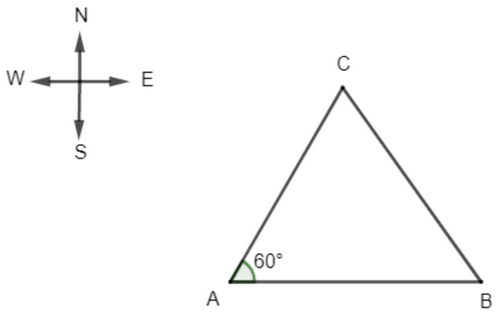
A là vị trí cảng.
Ca nô đi theo hướng đông từ A đến B, sau 3 giờ đi được quãng đường AB = 50.3 = 150 (km).
Tàu cá đi theo hướng N300E từ A đến C, sau 3 giờ đi được quãng đường AC = 40.3 = 120 (km).
Áp dụng định lí Cosin trong tam giác ABC ta có:
\(\begin{array}{*{20}{l}}{B{C^2} = A{B^2} + A{C^2} – 2AB.AC.\cos {{60}^{}}}\\{{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} = {{150}^2} + {{120}^2} – 2.150.120.\frac{1}{2}}\\{{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} = 18{\kern 1pt} 900}\\{ \Rightarrow BC = 30\sqrt {21} \approx 137,5.}\end{array}\)
Vậy sau 3 giờ hai tàu cách nhau khoảng 137,5km.
Chọn D.
Câu 26.
Cách giải
Sử dụng máy tính cầm tay, ta được \(\sqrt 3 = 1,7320508076…\)
Làm tròn đến hàng phần nghìn ta được kết quả: $1,732$.
Chọn B.
Câu 27.
Cách giải
Ta có: \(h = 347,13{\rm{m}} \pm 0,2{\rm{m}} \Rightarrow d = 0,2\)
Độ chính xác d có chữ số (khác 0) ở hàng lớn nhất là hàng phần mười, do đó ta làm tròn số gần đúng \(h = 347,13\) đến hàng đơn vị, kết quả là $347$.
Chọn B
Câu 28 (TH)
Hướng dẫn:
Trung bình
\(\bar x = \frac{{{m_1}{x_1} + {m_2}{x_2} + … + {m_k}{x_k}}}{n}\) trong đó mk là tần số của giá trị xk và \(n = {m_1} + {m_2} + … + {m_k}\)
Cách giải:
Khối lượng trung bình của cả ba nhóm học sinh là: \(\bar x = \frac{{20.50 + 15.38 + 25.40}}{{20 + 15 + 25}} = 42,8.\)
Chọn B.
Câu 29 (VD):
Hướng dẫn:
Áp dụng công thức tìm phương sai và độ lệch chuẩn.
Cách giải:
Số trung bình cộng:
\(\bar x = \frac{{9.1 + 10.1 + 11.3 + 12.5 + 13.8 + 14.13 + 15.19 + 16.24 + 17.14 + 18.10 + 19.2}}{{100}}\)\( = \frac{{1523}}{{100}} = 15,23\) (điểm)
Phương sai:
\({s^2} = \frac{1}{{100}}\left[ {1.{{\left( {9 – 15,23} \right)}^2} + 1.{{\left( {10 – 15,23} \right)}^2} + \; \ldots \; + 10.{{\left( {18 – 15,23} \right)}^2} + 2.{{\left( {19 – 15,23} \right)}^2}} \right]\) \( = 3,9571\)(điểm)
Độ lệch chuẩn:
\(s = \sqrt {{s^2}} \)\( = \sqrt {3,9571} \; \approx 1,989{\rm{2}}\) (điểm)
Vậy phương sai nhỏ hơn \(4\), độ lệch chuẩn nhỏ hơn \(2\).
Chọn D.
Câu 30.
Cách giải:
Ta có \(\left\{ {\begin{array}{*{20}{l}}{\left| {\overrightarrow {AB} – \overrightarrow {AD} } \right| = \left| {\overrightarrow {DB} } \right| = BD}\\{\left| {\overrightarrow {AB} + \overrightarrow {AD} } \right| = \left| {\overrightarrow {AC} } \right| = AC}\end{array}} \right..\)
Mà \(BD = AC \Rightarrow \left| {\overrightarrow {AB} – \overrightarrow {AD} } \right| = \left| {\overrightarrow {AB} + \overrightarrow {AD} } \right|.\)
Chọn C.
Câu 31.
Cách giải:
Ta có \(\overrightarrow {MA} – \overrightarrow {MB} + \overrightarrow {MC} = \vec 0 \Leftrightarrow \overrightarrow {BA} + \overrightarrow {MC} = \vec 0 \Leftrightarrow \overrightarrow {MC} = \overrightarrow {AB} \)
\( \Rightarrow MABC\) là hình bình hành
\( \Rightarrow \overrightarrow {MA} = \overrightarrow {CB} .\)
Do đó D sai.
Chọn D.
Câu 32.
Cách giải:
Vì ABCD là hình bình hành nên \(\overrightarrow {AB} = \overrightarrow {DC} \) hay \(\overrightarrow {AB} + \overrightarrow {CD} = \vec 0\)
Ta có: \(\left\{ {\begin{array}{*{20}{l}}{\overrightarrow {AC} = \overrightarrow {AB} + \overrightarrow {BC} }\\{\overrightarrow {BD} = \overrightarrow {BC} + \overrightarrow {CD} }\end{array}} \right.\)\( \Rightarrow \overrightarrow {AC} + \overrightarrow {BD} = 2\overrightarrow {BC} + \overrightarrow {AB} + \overrightarrow {CD} = 2\overrightarrow {BC} \)
Vậy A đúng.
\(\overrightarrow {AC} + \overrightarrow {CB} = \overrightarrow {AB} \) => B sai.
\(\overrightarrow {AC} – \overrightarrow {BD} = \overrightarrow {AB} – \overrightarrow {CD} = \overrightarrow {DC} + \overrightarrow {DC} = 2\overrightarrow {DC} = – 2\overrightarrow {CD} \) => C sai
\(\overrightarrow {AC} – \overrightarrow {AD} = \overrightarrow {DC} \) => D sai.
Chọn A.
Câu 33.
Cách giải:
Ta có: \(OA = OB = a\)
\( \Rightarrow \left| {2\overrightarrow {OA} } \right| + \left| {3\overrightarrow {OB} } \right| = 2a + 3a = 5a\). Vậy B đúng.
Tương tự, ta có \(\left| {11\overrightarrow {OA} } \right| – \left| {6\overrightarrow {OB} } \right| = 11a – 6a = 5a\). Do đó D đúng.
Lấy C, D sao cho \(\overrightarrow {OC} = 3\overrightarrow {OA} ;\overrightarrow {OD} = 4\overrightarrow {OB} ;\)
Dựng hình bình hành OCED. Do \(\widehat {AOB} = {90^^\circ }\) nên OCED là hình chữ nhật.
Ta có: \(3\overrightarrow {OA} + 4\overrightarrow {OB} = \overrightarrow {OC} + \overrightarrow {OD} = \overrightarrow {OE} \)
\( \Rightarrow \left| {3\overrightarrow {OA} + 4\overrightarrow {OB} } \right| = \left| {\overrightarrow {OE} } \right| = OE\)
Lại có: \(OC = 3OA = 3a,OD = 4OB = 4a.\)
\( \Rightarrow OE = \sqrt {O{C^2} + C{E^2}} = \sqrt {O{C^2} + O{D^2}} = \sqrt {{{(3a)}^2} + {{(4a)}^2}} = 5a\)
Do đó A đúng.
Chọn C
Câu 34.
Cách giải:
Vì M là trung điểm của BC suy ra \(\overrightarrow {AB} + \overrightarrow {AC} = 2\overrightarrow {AM} \)
Khi đó \(\overrightarrow {AM} .\overrightarrow {BC} = \frac{1}{2}\left( {\overrightarrow {AB} + \overrightarrow {AC} } \right).\overrightarrow {BC} = \frac{1}{2}\left( {\overrightarrow {AB} + \overrightarrow {AC} } \right).\left( {\overrightarrow {BA} + \overrightarrow {AC} } \right)\)
\( = \frac{1}{2}\left( {\overrightarrow {AB} + \overrightarrow {AC} } \right).\left( {\overrightarrow {AC} – \overrightarrow {AB} } \right) = \frac{1}{2}\left( {{{\overrightarrow {AC} }^2} – {{\overrightarrow {AB} }^2}} \right) = \frac{1}{2}\left( {A{C^2} – A{B^2}} \right) = \frac{{{b^2} – {c^2}}}{2}\)
Chọn A.
Câu 35.
Cách giải:
Ta có \(\left\{ \begin{array}{l}BD = a\sqrt 2 \\\overrightarrow {BC} + \overrightarrow {BD} + \overrightarrow {BA} = \left( {\overrightarrow {BC} + \overrightarrow {BA} } \right) + \overrightarrow {BD} = \overrightarrow {BD} + \overrightarrow {BD} = 2\overrightarrow {BD} \end{array} \right.\)
Khi đó \(P = \left( {\overrightarrow {AB} + \overrightarrow {AC} } \right).2\overrightarrow {BD} = 2\overrightarrow {AB} .\overrightarrow {BD} + 2\overrightarrow {AC} .\overrightarrow {BD} = – 2\overrightarrow {BA} .\overrightarrow {BD} + \vec 0\)
\( = – 2BA.BD\cos \left( {\overrightarrow {BA} ,\overrightarrow {BD} } \right) = – 2.a.a\sqrt 2 .\frac{{\sqrt 2 }}{2} = – 2{a^2}\)
Chọn D.
II. Tự luận (3 điểm)
Câu 1 (TH):
Cách giải:
a) Ta có:
\( = \overrightarrow {{\rm{MA}}} \cdot (\overrightarrow {{\rm{MC}}} – \overrightarrow {{\rm{MB}}} ) + \overrightarrow {{\rm{MB}}} (\overrightarrow {{\rm{MA}}} – \overrightarrow {{\rm{MC}}} ) + \overrightarrow {{\rm{MC}}} (\overrightarrow {{\rm{MB}}} – \overrightarrow {{\rm{MA}}} ) = \)
\( = \overrightarrow {{\rm{MA}}} \cdot \overrightarrow {{\rm{MC}}} – \overrightarrow {{\rm{MA}}} \cdot \overrightarrow {{\rm{MB}}} + \overrightarrow {{\rm{MB}}} \cdot \overrightarrow {{\rm{MA}}} – \overrightarrow {{\rm{MB}}} \cdot \overrightarrow {{\rm{MC}}} + \overrightarrow {{\rm{MC}}} \cdot \overrightarrow {{\rm{MB}}} – \overrightarrow {{\rm{MC}}} \cdot \overrightarrow {{\rm{MA}}} \)
\( = \overrightarrow {{\rm{MA}}} \cdot \overrightarrow {{\rm{MC}}} – \overrightarrow {{\rm{MC}}} \cdot \overrightarrow {{\rm{MA}}} – \overrightarrow {{\rm{MA}}} \cdot \overrightarrow {{\rm{MB}}} + \overrightarrow {{\rm{MB}}} \cdot \overrightarrow {{\rm{MA}}} – \overrightarrow {{\rm{MB}}} \cdot \overrightarrow {{\rm{MC}}} + \overrightarrow {{\rm{MC}}} \cdot \overrightarrow {{\rm{MB}}} = 0\)
b)
\({\rm{M}}{{\rm{A}}^2} = {\overrightarrow {{\rm{MA}}} ^2} = {(\overrightarrow {{\rm{MG}}} + \overrightarrow {{\rm{GA}}} )^2} = {\rm{M}}{{\rm{G}}^2} + {\rm{G}}{{\rm{A}}^2} + 2\overrightarrow {{\rm{MG}}} \cdot \overrightarrow {{\rm{GA}}} \)
\({\rm{M}}{{\rm{B}}^2} = {\overrightarrow {{\rm{MB}}} ^2} = {(\overrightarrow {{\rm{MG}}} + \overrightarrow {{\rm{GB}}} )^2} = {\rm{M}}{{\rm{G}}^2} + {\rm{G}}{{\rm{B}}^2} + 2\overrightarrow {{\rm{MG}}} \cdot \overrightarrow {{\rm{GB}}} \)
\({\rm{M}}{{\rm{C}}^2} = {\overrightarrow {{\rm{MC}}} ^2} = {(\overrightarrow {{\rm{MG}}} + \overrightarrow {{\rm{GC}}} )^2} = {\rm{M}}{{\rm{G}}^2} + {\rm{G}}{{\rm{C}}^2} + 2\overrightarrow {{\rm{MG}}} \cdot \overrightarrow {{\rm{GC}}} \)
\( \Rightarrow {\rm{M}}{{\rm{A}}^2} + {\rm{M}}{{\rm{B}}^2} + {\rm{M}}{{\rm{C}}^2} = 3{\rm{M}}{{\rm{G}}^2} + {\rm{G}}{{\rm{A}}^2} + {\rm{G}}{{\rm{B}}^2} + {\rm{G}}{{\rm{C}}^2} + 2(\overrightarrow {{\rm{MG}}} \cdot \overrightarrow {{\rm{GA}}} + \overrightarrow {{\rm{MG}}} \cdot \overrightarrow {{\rm{GB}}} + \overrightarrow {{\rm{MG}}} \cdot \overrightarrow {{\rm{GC}}} )\)
\( = 3{\rm{M}}{{\rm{G}}^2} + {\rm{G}}{{\rm{A}}^2} + {\rm{G}}{{\rm{B}}^2} + {\rm{G}}{{\rm{C}}^2} + 2\overrightarrow {{\rm{MG}}} (\overrightarrow {{\rm{GA}}} + \overrightarrow {{\rm{GB}}} + \overrightarrow {{\rm{GC}}} ) = 3{\rm{M}}{{\rm{G}}^2} + {\rm{G}}{{\rm{A}}^2} + {\rm{G}}{{\rm{B}}^2} + {\rm{G}}{{\rm{C}}^2}\)
c) Vì \({\rm{M}}{{\rm{A}}^2} + {\rm{M}}{{\rm{B}}^2} + {\rm{M}}{{\rm{C}}^2} = 3{\rm{M}}{{\rm{G}}^2} + {\rm{G}}{{\rm{A}}^2} + {\rm{G}}{{\rm{B}}^2} + {\rm{G}}{{\rm{C}}^2}\) đúng với M bất kì.
Chọn \({\rm{M}} \equiv {\rm{A}}\) ta được:
\({\rm{A}}{{\rm{A}}^2} + {\rm{A}}{{\rm{B}}^2} + {\rm{A}}{{\rm{C}}^2} = 3{\rm{A}}{{\rm{G}}^2} + {\rm{G}}{{\rm{A}}^2} + {\rm{G}}{{\rm{B}}^2} + {\rm{G}}{{\rm{C}}^2}\)
\( \Leftrightarrow {\rm{A}}{{\rm{B}}^2} + {\rm{A}}{{\rm{C}}^2} = 4{\rm{G}}{{\rm{A}}^2} + {\rm{G}}{{\rm{B}}^2} + {\rm{G}}{{\rm{C}}^2}\)
Tương tự,
\({\rm{M}} \equiv {\rm{B}} \Rightarrow {\rm{B}}{{\rm{A}}^2} + {\rm{B}}{{\rm{C}}^2} = 4\;{\rm{G}}{{\rm{B}}^2} + {\rm{G}}{{\rm{A}}^2} + {\rm{G}}{{\rm{C}}^2}\)
\({\rm{M}} \equiv {\rm{C}} \Rightarrow {\rm{C}}{{\rm{B}}^2} + {\rm{A}}{{\rm{C}}^2} = 4{\rm{G}}{{\rm{C}}^2} + {\rm{G}}{{\rm{B}}^2} + {\rm{G}}{{\rm{A}}^2}\)
Thay \(AB = c,AC = b,BC = a\)
\(\begin{array}{*{20}{l}}{ \Rightarrow 6\left( {{\rm{G}}{{\rm{A}}^2} + {\rm{G}}{{\rm{B}}^2} + {\rm{G}}{{\rm{C}}^2}} \right) = 2\left( {{{\rm{a}}^2} + {{\rm{b}}^2} + {{\rm{c}}^2}} \right)}\\{ \Leftrightarrow {\rm{G}}{{\rm{A}}^2} + {\rm{G}}{{\rm{B}}^2} + {\rm{G}}{{\rm{C}}^2} = \frac{1}{3}\left( {{{\rm{a}}^2} + {{\rm{b}}^2} + {{\rm{c}}^2}} \right)}\end{array}\)
Câu 2 (VD):
Cách giải:
Từ giả thiết, ta suy ra tam giác ABC có
\(\widehat {CAB} = {60^^\circ },\widehat {ABC} = {105^^\circ }30’\)và \(c = 70\)
Khi đó \(\hat A + \hat B + \hat C = {180^^\circ } \Leftrightarrow \hat C = {180^^\circ } – \left( {\hat A + \hat B} \right) = {180^^\circ } – {165^^\circ }30′ = {14^^\circ }30’\)
Theo định lí sin, ta có \(\frac{b}{{\sin B}} = \frac{c}{{\sin C}}\) hay \(\frac{b}{{\sin {{105}^^\circ }30′}} = \frac{{70}}{{\sin {{14}^^\circ }30′}}\)
Do đó \(AC = b = \sin {105^^\circ }30’\frac{{70}}{{\sin {{14}^^\circ }30′}} \approx 269,4m\)
Gọi CH là khoảng cách từ C đến mặt đất. Tam giác vuông ACH có cạnh CH đối diện với góc \({30^^\circ }\) nên \(CH = \frac{{AC}}{2} = \frac{{269,4}}{2} = 134,7m\)
Vậy ngọn núi cao khoảng 135m.
Câu 3 (VDC):
Hướng dẫn:
Thay \(x = {30^0}\), sử dụng mối quan hệ giá trị lượng giác của hai góc bù nhau.
Cách giải:
Thay \(x = {30^0}\) ta có:
\(\begin{array}{*{20}{l}}{P = 4\tan \left( {{{30}^0} + {4^0}} \right).\sin {{30}^0}\cot \left( {{{4.30}^0} + {{26}^0}} \right) + \frac{{8{{\tan }^2}\left( {{3^0} – {{30}^0}} \right)}}{{1 + {{\tan }^2}\left( {{{5.30}^0} + {3^0}} \right)}} + 8{{\cos }^2}\left( {{{30}^0} – {3^0}} \right)}\\{P = 4\tan {{34}^0}.\sin {{30}^0}\cot {{146}^0} + \frac{{8{{\tan }^2}\left( { – {{27}^0}} \right)}}{{1 + {{\tan }^2}{{153}^0}}} + 8{{\cos }^2}{{27}^0}}\\{P = 4\tan {{34}^0}.\sin {{30}^0}\cot \left( {{{180}^0} – {{34}^0}} \right) + 8{{\tan }^2}{{27}^0}{{\cos }^2}{{153}^0} + 8{{\cos }^2}{{27}^0}}\\{P = – 4\tan {{34}^0}.\sin {{30}^0}\cot {{34}^0} + 8{{\tan }^2}{{27}^0}{{\cos }^2}\left( {{{180}^0} – {{27}^0}} \right) + 8{{\cos }^2}{{27}^0}}\\{P = – 4.\sin {{30}^0} + 8{{\tan }^2}{{27}^0}{{\cos }^2}{{27}^0} + 8{{\cos }^2}{{27}^0}}\\{P = – 4.\sin {{30}^0} + 8{{\cos }^2}{{27}^0}\left( {{{\tan }^2}{{27}^0} + 1} \right)}\\{P = – 4.\sin {{30}^0} + 8{{\cos }^2}{{27}^0}\frac{1}{{{{\cos }^2}{{27}^0}}}}\\{P = – 4.\frac{1}{2} + 8}\\{P = 6}\end{array}\)