Giải Giải đề 10 Tổng hợp 10 đề thi học kì 1 Toán 10 kết nối tri thức – Đề thi đề kiểm tra Toán lớp 10 Kết nối tri thức.
Câu hỏi/Đề bài:
I. Phần trắc nghiệm (6 điểm – 24 câu)
|
1.C |
2.C |
3.D |
4.D |
5.A |
6.B |
7.C |
8.C |
|
9.B |
10.C |
11.A |
12.C |
13.C |
14.C |
15.D |
16.C |
|
17.B |
18.B |
19.D |
20.B |
21.B |
22.D |
23.B |
24.D |
Câu 1 (TH):
Hướng dẫn:
Mệnh đề chưa biến sai khi tìm được ít nhất 1 giá trị không thỏa mãn.
Cách giải:
Dùng phương pháp loại trừ
A sai khi \(x = \frac{1}{2}\), B sai vì x = -4 không thỏa mãn, D sai do \(a = \sqrt 2 \)không là số hữu tỉ
Chọn C.
Câu 2 (TH):
Hướng dẫn:
Phủ định của \(\forall \) là \(\exists \), phủ định của < là \( \ge \)
Cách giải:
Phủ định của \(\forall x \in \mathbb{R},{x^2} – x + 2023 < 0\) là \(\exists x \in \mathbb{R},{x^2} – x + 2023 \ge 0\).
Chọn C.
Câu 3 (NB):
Hướng dẫn:
Kí hiệu \( \in \) để chỉ phần tử thuộc tập hợp.
Kí hiệu \( \subset \) để chỉ tập hợp là tập hợp con của 1 tập hợp.
Cách giải:
D sai do \(\left\{ 3 \right\}\)là 1 tập hợp nên ta không dùng kí hiệu \( \in \).
Chọn D.
Câu 4 (TH):
Hướng dẫn:
phương trình \(2{x^2} – 5x + 3 = 0\) và đối chiếu điều kiện của x
Cách giải:
\(2{x^2} – 5x + 3 = 0 \Leftrightarrow \left[ \begin{array}{l}x = \frac{3}{2} \in \mathbb{R}\\x = 1 \in \mathbb{R}\end{array} \right. \Rightarrow A = \left\{ {1;\frac{3}{2}} \right\}\)
Chọn D.
Câu 5 (TH):
Hướng dẫn:
Áp dụng định nghĩa tìm các phép toán trên tập hợp.
Cách giải:
\(B = \left\{ {x \in \mathbb{N}:{x^2} – 4 = 0} \right\} = \left\{ 2 \right\} \Rightarrow A \cap B = \left\{ 2 \right\}\)
Chọn A.
Câu 6 (TH): –
Hướng dẫn:
Biểu diễn các tập hợp trên trục số và áp dụng định nghĩa các phép toán trên tập hợp.
Cách giải:

Chọn B.
Câu 7 (NB):
Hướng dẫn:
Thay tọa độ các điểm vào bất phương trình và kiểm tra tính đúng sai.
Cách giải:
Vì 4 + 2.2=8 > 4 nên \(\left( {4;2} \right)\) không thuộc miền nghiệm của bất phương trình \(x + 2y < 4\).
Chọn C.
Câu 8 (TH):
Hướng dẫn:
Thay tọa độ các điểm vào bất phương trình và kiểm tra tính đúng sai
Cách giải:
Vì \(\left( {0; – 2} \right)\)thỏa mãn cả 3 phương trình nên \(\left( {0; – 2} \right)\) thuộc miền nghiệm của hệ bất phương trình.
Chọn C.
Câu 9 (NB):
Hướng dẫn:
Kích thước mẫu là số phần tử của 1 mẫu số liệu
Cách giải:
Có tất cả 20 mẫu số liệu thống kê nên kích thước mẫu bằng 20.
Chọn B.
Câu 10 (TH):
Hướng dẫn:
Tần suất \({f_i}\)của giá trị \({x_i}\) là tỉ số giữa tần số n và kích thước mẫu N có công thức \({f_i} = \frac{n}{N}\).
Cách giải:
\({f_i} = \frac{{80}}{{400}} = 0,2 = 20\% \)
Chọn C.
Câu 11 (TH):
Hướng dẫn:
Số trung bình là \(\overline x = \frac{{{x_1} + {x_2} + {x_3} + … + {x_n}}}{n}\)
Cách giải:
\(\overline x = \frac{{3.2 + 4.3 + 5.7 + 6.18 + 7.3 + 8.2 + 9.4 + 10.1}}{{40}} = 6,1\)
Chọn A.
Câu 12 (TH):
Hướng dẫn:
Độ lệch chuẩn là căn bậc hai của phương sai
Cách giải:
Chọn C.
Câu 13 (TH):
Hướng dẫn:
Dùng MTCT để tính
Cách giải:
Chọn C.
Câu 14 (TH):
Hướng dẫn:
Dùng MTCT để tính
Cách giải:
Chọn C.
Câu 15 (NB):
Hướng dẫn:
Dùng bảng các giá trị lượng giác đặc biệt.
Cách giải:
\(\cos {60^{\rm{o}}} + \sin {30^{\rm{o}}} = \frac{1}{2} + \frac{1}{2} = 1\)
Chọn D.
Câu 16 (NB):
Hướng dẫn:
Dùng định lý cosin \({b^2} = {a^2} + {c^2} – 2ac.\cos B\)
Cách giải:
\({b^2} = {a^2} + {c^2} – 2ac.\cos B = {8^2} + {3^2} – 2.3.8.\cos 60 = 49 \Rightarrow b = 7\)
Chọn C.
Câu 17 (TH):
Hướng dẫn:
Dùng định lý cosin \(\cos A = \frac{{{b^2} + {c^2} – {a^2}}}{{2bc}}\)
Cách giải:
\(\cos A = \frac{{{b^2} + {c^2} – {a^2}}}{{2bc}} = \frac{{{b^2} + {c^2} – \left( {{b^2} + {c^2} – bc} \right)}}{{2bc}} = \frac{1}{2} \Rightarrow \angle A = {60^0}\)
Chọn B.
Câu 18 (TH):
Hướng dẫn:
Dùng định lý sin: \(\frac{a}{{\sin A}} = \frac{b}{{\sin B}} = \frac{c}{{\sin C}} = 2R\)
Cách giải:
\(\frac{a}{{\sin A}} = 2R \Leftrightarrow \frac{{\sqrt 3 }}{{\sin 60}} = 2R \Rightarrow R = 1\)
Chọn B.
Câu 19 (NB):
Hướng dẫn:
Dùng định lý về 3 điểm thẳng hàng.
Cách giải:
D sai do khi k = 0 thì \(\overrightarrow {AB} = \overrightarrow 0 \)
Chọn D.
Câu 20 (TH):
Hướng dẫn:
Dùng quy tắc cộng, trừ hai vecto
Cách giải:
\(\begin{array}{l}\overrightarrow {MN} + \overrightarrow {PQ} + \overrightarrow {RN} + \overrightarrow {NP} + \overrightarrow {QR} = \overrightarrow {MN} + \overrightarrow {NP} + \overrightarrow {PQ} + \overrightarrow {QR} + \overrightarrow {RN} \\\,\, = \overrightarrow {MP} + \overrightarrow {PR} + \overrightarrow {RN} = \overrightarrow {MR} + \overrightarrow {RN} = \overrightarrow {MN} \end{array}\)
Chọn B.
Câu 21 (VD):
Hướng dẫn:
Dùng quy tắc cộng, trừ hai vecto
Cách giải:
\(\overrightarrow {OB} – \overrightarrow {OC} = \overrightarrow {CB} ,\,\,\overrightarrow {OD} – \overrightarrow {OA} = \overrightarrow {AD} \)mà \(\overrightarrow {CB} ,\,\,\overrightarrow {AD} \)là 2 vecto ngược hướng nên B sai
Chọn B.
Câu 22 (VD):
Hướng dẫn:
Nếu M là trung điểm của AB thì với mọi điểm O là luôn có \(\overrightarrow {OA} + \overrightarrow {OB} = 2\overrightarrow {OM} \)
Cách giải:
Gọi M là trung điểm của AC khi đó \(\overrightarrow {AB} + \overrightarrow {AC} = 2\overrightarrow {AM} \). Do G là trọng tâm tam giác ABC nên \(\overrightarrow {AG} = \frac{2}{3}\overrightarrow {AM} \). Suy ra \(\overrightarrow {AG} = \frac{2}{3}.\frac{1}{2}\left( {\overrightarrow {AB} + \overrightarrow {AC} } \right) = \frac{1}{3}\left( {\overrightarrow {AB} + \overrightarrow {AC} } \right)\)
Chọn D.
Câu 23 (TH):
Hướng dẫn:
\(\overrightarrow a .\overrightarrow b = \left| {\overrightarrow a } \right|.\left| {\overrightarrow b } \right|.\cos \left( {\overrightarrow a ,\,\overrightarrow b } \right)\)
Cách giải:
\(\overrightarrow {AB} .\overrightarrow {BC} = \left| {\overrightarrow {AB} } \right|.\left| {\overrightarrow {BC} } \right|.\cos \left( {\overrightarrow {AB} ,\,\overrightarrow {BC} } \right) = 4.4.\cos 120 = – 8\)
Chọn B.
Câu 24 (VD):
Hướng dẫn:
Cách giải:
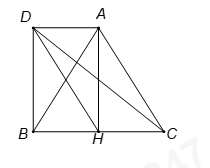
Gọi \(D\) là điểm thỏa mãn tứ giác \(ACHD\) là hình bình hành
\( \Rightarrow AHBD\) là hình chữ nhật.
\(\left| {\overrightarrow {CA} – \overrightarrow {HC} } \right| = \left| {\overrightarrow {CA} + \overrightarrow {CH} } \right| = \left| {\overrightarrow {CD} } \right| = CD.\)
Ta có \(CD = \sqrt {B{D^2} + B{C^2}} = \sqrt {A{H^2} + B{C^2}} = \sqrt {\frac{{3{a^2}}}{4} + {a^2}} = \frac{{a\sqrt 7 }}{2}.\)
Chọn D.
II. Phần tự luận (4 điểm)
Câu 1 (VD):
Hướng dẫn:
Dùng các phép toán trên tập hợp
Cách giải:
Gọi tập hợp các học sinh giỏi Toán là A. Khi đó n(A)=10
Gọi tập hợp các học sinh giỏi Lý là B. Khi đó n(B)=15
Số học sinh học giỏi toán hoặc giỏi lý là \(n\left( {A \cup B} \right)\) là 40 – 22=18 học sinh
Vậy số học sinh giỏi cả 2 môn Toán Lý là \(n\left( {A \cap B} \right) = n\left( A \right) + n\left( B \right) – n\left( {A \cup B} \right) = 10 + 15 – 18 = 7\)
Vậy có tất cả 7 học sinh vừa giỏi Toán vừa giỏi Lý.
Câu 2 (TH):
Hướng dẫn:
Dùng các định cosin, công thức diện tích tỏng tam giác.
Cách giải:
Ta có \(B{C^2} = A{B^2} + A{C^2} – 2AB.AC.\cos A = 23,{8^2} + 31,{9^2} – 2.23,8.31,9.\cos 83,6 = 1414,791\)
Suy ra \(BC \approx 37,61\)km
Gọi khoảng cách từ máy bay A đến mặt nước biển là d. Khi đó áp dụng công thức diện tích tam giác ta có
\(\begin{array}{l}S = \frac{1}{2}.AB.AC.\sin A = \frac{1}{2}.d.BC\\ \Leftrightarrow d = \frac{{AB.AC.\sin A}}{{BC}} = \frac{{23,8.31,9.\sin 83,6}}{{37,61}} \approx 20,06\end{array}\)
Vậy khoảng cách giữa hai tàu BC là 37,61km và độ cao của máy bay A so với mặt nước biển là 20,06km.
Câu 3 (VD):
Hướng dẫn:
Nếu M là trung điểm của AB thì với mọi điểm O là luôn có \(\overrightarrow {OA} + \overrightarrow {OB} = 2\overrightarrow {OM} \)
Cách giải:
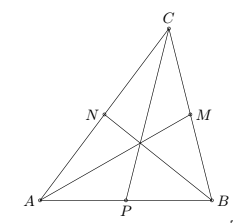
a. Ta có \(\overrightarrow {AM} = \frac{1}{2}\left( {\overrightarrow {AC} + \overrightarrow {AB} } \right),\,\overrightarrow {BN} = \frac{1}{2}\left( {\overrightarrow {BC} + \overrightarrow {BA} } \right),\,\overrightarrow {CP} = \frac{1}{2}\left( {\overrightarrow {CA} + \overrightarrow {CB} } \right)\) nên
\(\begin{array}{l}\overrightarrow {AM} + \overrightarrow {BN} + \overrightarrow {CP} = \frac{1}{2}\left( {\overrightarrow {AC} + \overrightarrow {AB} } \right) + \frac{1}{2}\left( {\overrightarrow {BC} + \overrightarrow {BA} } \right) + \frac{1}{2}\left( {\overrightarrow {CA} + \overrightarrow {CB} } \right)\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \frac{1}{2}\left( {\overrightarrow {AC} + \overrightarrow {AB} + \overrightarrow {BC} + \overrightarrow {BA} + \overrightarrow {CA} + \overrightarrow {CB} } \right)\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \frac{1}{2}.\overrightarrow 0 = \overrightarrow 0 \end{array}\)(đpcm)
b. Vì P là trung điểm của AB nên \(\overrightarrow {AP} = \overrightarrow {PB} \). Khi đó ta có \(\overrightarrow {AP} + \overrightarrow {BM} = \overrightarrow {PB} + \overrightarrow {BM} = \overrightarrow {PM} \).
Mà PM là đường trung bình trong tam giác ABC nên suy ra \(\overrightarrow {PM} = \frac{1}{2}\overrightarrow {AC} \).
Suy ra \(\overrightarrow {AP} + \overrightarrow {BM} = \frac{1}{2}\overrightarrow {AC} \) (đpcm).