Trả lời Đề thi giữa kì 2 Toán 10 Kết nối tri thức – Đề số 1 – Đề thi giữa kì 2 – Đề số 1 – Đề thi đề kiểm tra Toán lớp 10 Kết nối tri thức. Phần trắc nghiệm (7 điểm) Câu 1: Tập xác định của hàm số \( y = \frac{x+1}{x-1}\) là:…
Đề thi:
Phần trắc nghiệm (7 điểm)
Câu 1: Tập xác định của hàm số \(y = \frac{{x + 1}}{{x – 1}}\) là:
A. \(\mathbb{R}\backslash \left\{ { \pm 1} \right\}\).
B. \(\mathbb{R}\backslash \left\{ { – 1} \right\}\).
C. \(\mathbb{R}\backslash \left\{ 1 \right\}\).
D. \(\left( {1; + \infty } \right)\).
Câu 2: Trong các hàm số sau, hàm số nào nghịch biến trên \(\mathbb{R}\)?
A. \(y = x\).
B. \(y = – 2x\).
C. \(y = 2x\).
D. \(y = \frac{1}{2}x\)
Câu 3: Cho hàm số \(f\left( x \right) = \sqrt {2{x^2} + 1} \). Giá trị \(f\left( { – 2} \right)\) bằng
A. \( – 3\).
B. \(3\).
C. \(4\).
D. Không xác định.
Câu 4: Khoảng đồng biến của hàm số \(y = {x^2} – 4x + 3\)là
A. \(\left( { – \infty ; – 2} \right)\).
B. \(\left( { – \infty ;2} \right)\).
C. \(\left( { – 2; + \infty } \right)\).
D. \(\left( {2; + \infty } \right)\).
Câu 5: Trục đối xứng của đồ thị hàm số \(y = a{x^2} + bx + c\), \((a \ne 0)\) là đường thẳng nào dưới đây?
A. \(x = – \frac{b}{{2a}}.\)
B. \(x = – \frac{c}{{2a}}.\)
C. \(x = – \frac{\Delta }{{4a}}.\)
D. \(x = \frac{b}{{2a}}\).
Câu 6: Cho parabol \(y = a{x^2} + bx + c\) có đồ thị như hình vẽ dưới đây. Khẳng định nào dưới đây đúng?
A. \(a > 0.\)
B. \(a < 0.\)
C. \(a = 1.\)
D. \(a = 2.\)
Câu 7: Cho \(f\left( x \right) = a{x^2} + bx + c\), \(\left( {a \ne 0} \right)\) và \(\Delta = {b^2} – 4ac\). Cho biết dấu của \(\Delta \) khi \(f\left( x \right)\) luôn cùng dấu với hệ số \(a\) với mọi \(x \in \mathbb{R}\).
A. \(\Delta < 0\).
B. \(\Delta = 0\).
C. \(\Delta > 0\).
D. \(\Delta \ge 0\).
Câu 8: Tập nghiệm \(S\) của bất phương trình \({x^2} – x – 6 \le 0\).
A. \(S = \left( { – \infty ; – 3} \right) \cup \left( {2: + \infty } \right)\).
B. \(\left[ { – 2;3} \right]\).
C. \(\left[ { – 3;2} \right]\).
D. \(\left( { – \infty ; – 3} \right] \cup \left[ {2; + \infty } \right)\).
Câu 9: Tìm tập nghiệm \(S\) của bất phương trình \({x^2} – 4x + 4 > 0\).
A. \(S = \mathbb{R}\backslash \left\{ 2 \right\}\).
B. \(S = \mathbb{R}\).
C. \(S = \left( {2; + \infty } \right)\).
D. \(S = \mathbb{R}\backslash \left\{ { – 2} \right\}\).
Câu 10: Phương trình \(\sqrt {x – 1} = x – 3\) có tập nghiệm là
A. \(S = \left\{ 5 \right\}\).
B. \(S = \left\{ {2;5} \right\}\).
C. \(S = \left\{ 2 \right\}\).
D. \(S = \emptyset \).
Câu 11: Số nghiệm của phương trình \(\sqrt {{x^2} – 4x + 3} = \sqrt {1 – x} \)là
A. Vô số.
B. 2.
C. 1.
D. 0.
Câu 12: Trong mặt phẳng \(Oxy\), đường thẳng \(\left( d \right):\,\,ax + by + c = 0,\,\,\,\left( {{a^2} + {b^2} \ne 0} \right)\). Vectơ nào sau đây là một vectơ pháp tuyến của đường thẳng \(\left( d \right)\)?
A. \(\overrightarrow n = \left( {a; – b} \right)\).
B. \(\overrightarrow n = \left( {b;a} \right)\).
C. \(\overrightarrow n = \left( {b; – a} \right)\).
D. \(\overrightarrow n = \left( {a;b} \right)\).
Câu 13: Phương trình tham số của đường thẳng đi qua hai điểm \(A\left( {2; – 1} \right)\) và \(B\left( {2;5} \right)\) là
A. \(\left\{ \begin{array}{l}x = 2t\\y = – 6t\end{array} \right.\).
B. \(\left\{ \begin{array}{l}x = 2 + t\\y = 5 + 6t\end{array} \right.\).
C. \(\left\{ \begin{array}{l}x = 1\\y = 2 + 6t\end{array} \right.\).
D. \(\left\{ \begin{array}{l}x = 2\\y = – 1 + 6t\end{array} \right.\).
Câu 14: Trong mặt phẳng \(Oxy\), đường thẳng \(d:\,x – 2y – 1 = 0\) song song với đường thẳng có phương trình nào sau đây?
A. \(x + 2y + 1 = 0\).
B. \(2x – y = 0\).
C. \( – x + 2y + 1 = 0\).
D. \( – 2x + 4y – 1 = 0\).
Câu 15: Tính góc giữa hai đường thẳng \(\Delta :x – \sqrt 3 y + 2 = 0\) và \(\Delta ‘:x + \sqrt 3 y – 1 = 0\).
A. \({90^ \circ }\).
B. \({120^ \circ }\).
C. \({60^ \circ }\).
D. \({30^ \circ }\).
Câu 16: Khoảng cách từ điểm \(M\left( {5\,;\, – 1} \right)\) đến đường thẳng \(3x + 2y + 13 = 0\) là:
A. \(2\sqrt {13} \).
B. \(\frac{{28}}{{\sqrt {13} }}\).
C. \(26\).
D. \(\frac{{\sqrt {13} }}{2}\).
Câu 17: Phương trình nào sau đây là phương trình đường tròn?
A. \({x^2} + {y^2} – 6x – 10y + 30 = 0\).
B. \({x^2} + {y^2} – 3x – 2y + 30 = 0\).
C. \(4{x^2} + {y^2} – 10x – 6y – 2 = 0\).
D. \({x^2} + 2{y^2} – 4x – 8y + 1 = 0\).
Câu 18: Phương trình nào sau đây là phương trình của đường tròn tâm \(I\left( { – 1;2} \right)\), bán kính bằng \(3\)?
A. \({\left( {x – 1} \right)^2} + {\left( {y + 2} \right)^2} = 9\).
B. \({\left( {x + 1} \right)^2} + {\left( {y + 2} \right)^2} = 9\).
C. \({\left( {x – 1} \right)^2} + {\left( {y – 2} \right)^2} = 9\).
D. \({\left( {x + 1} \right)^2} + {\left( {y – 2} \right)^2} = 9\).
Câu 19: Đường elip \(\frac{{{x^2}}}{9} + \frac{{{y^2}}}{7} = 1\) cắt trục tung tại hai điểm \({B_1}\), \({B_2}\). Độ dài \({B_1}{B_2}\) bằng
A. \(2\sqrt 7 \).
B. \(\sqrt 7 \).
C. \(3\).
D. \(6\).
Câu 20: Tọa độ các tiêu điểm của hypebol \(\left( H \right):\frac{{{x^2}}}{4} – \frac{{{y^2}}}{3} = 1\) là
A. \({F_1} = \left( { – 5;0} \right);{F_2} = \left( {5;0} \right)\).
B. \({F_1} = \left( {0; – 5} \right);{F_2} = \left( {0;5} \right)\).
C. \({F_1} = \left( {0; – \sqrt 7 } \right);{F_2} = \left( {0;\sqrt 7 } \right)\).
D. \({F_1} = \left( { – \sqrt 7 ;0} \right);{F_2} = \left( {\sqrt 7 ;0} \right)\).
Câu 21: Tập xác định của hàm số \(y = \sqrt {4 – x} + \sqrt {x – 2} \) là
A. \(D = \left( {2;4} \right)\)
B. \(D = \left[ {2;4} \right]\)
C. \(D = \left\{ {2;4} \right\}\)
D. \(D = \left( { – \infty ;2} \right) \cup \left( {4; + \infty } \right)\)
Câu 22: Cho hàm số có đồ thị như hình bên dưới.
Khẳng định nào sau đây là đúng?
A. Hàm số nghịch biến trên khoảng \(\left( {0;3} \right)\).
B. Hàm số đồng biến trên khoảng \(\left( { – \infty ;1} \right)\).
C. Hàm số nghịch biến trên khoảng \(\left( {0;2} \right)\).
D. Hàm số đồng biến trên khoảng \(\left( { – \infty ;3} \right)\).
Câu 23: Đồ thị hàm số \(y = f\left( x \right) = \left\{ \begin{array}{l}2x + 3{\rm{ }}\,\,\,khi{\rm{ }}x \le 2\\{x^2} – 3{\rm{ }}\,\,\,khi{\rm{ }}x > 2\end{array} \right.\) đi qua điểm có tọa độ nào sau đây ?
A. \(\left( {0; – 3} \right)\)
B. \(\left( {3;6} \right)\)
C. \(\left( {2;5} \right)\)
D. \(\left( {2;1} \right)\)
Câu 24: Cho parabol \(y = a{x^2} + bx + c\) có đồ thị như hình sau

Phương trình của parabol này là
A. \(y = – {x^2} + x – 1\).
B. \(y = 2{x^2} + 4x – 1\).
C. \(y = {x^2} – 2x – 1\).
D. \(y = 2{x^2} – 4x – 1\).
Câu 25: Tọa độ giao điểm của \(\left( P \right)\,:\,y = {x^2} – 4x\) với đường thẳng \(d\,:\,y = – x – 2\) là
A. \(M\left( {0;\, – 2} \right)\), \(N\left( {2;\, – 4} \right)\).
B. \(M\left( { – 1;\, – 1} \right)\), \(N\left( { – 2;\,0} \right)\).
C. \(M\left( {\, – 3;\,1} \right)\), \(N\left( {3;\, – 5} \right)\).
D. \(M\left( {1;\, – 3} \right)\), \(N\left( {2;\, – 4} \right)\).
Câu 26: Số nghiệm nguyên của bất phương trình \(2{x^2} – 3x – 15 \le 0\) là
A. \(6\).
B. \(5\).
C. \(8\).
D. \(7\).
Câu 27: Tìm tất cả các giá trị của tham số \(m\) để bất phương trình \({x^2} – \left( {m + 2} \right)x + 8m + 1 \le 0\) vô nghiệm.
A. \(m \in \left[ {0;28} \right]\).
B. \(m \in \left( { – \infty ;0} \right) \cup \left( {28; + \infty } \right)\).
C. \(m \in \left( { – \infty ;0} \right] \cup \left[ {28; + \infty } \right)\).
D. \(m \in \left( {0;28} \right)\).
Câu 28: Số nghiệm của phương trình \(\sqrt {{x^2} – 3x + 1} = 4x – 1\) là
A. \(0\).
B. \(3\).
C. \(2\).
D. \(1\).
Câu 29: Cho đường thẳng \(d\) có phương trình tham số \(\left\{ \begin{array}{l}x = 5 + t\\y = – 9 – 2t\end{array} \right.\). Phương trình tổng quát của đường thẳng \(d\) là
A. \(2x + y – 1 = 0\).
B. \( – 2x + y – 1 = 0\).
C. \(x + 2y + 1 = 0\).
D. \(2x + 3y – 1 = 0\).
Câu 30: Đường thẳng \(d\) đi qua điểm \(M\left( { – 2;1} \right)\) và vuông góc với đường thẳng \(\Delta :\left\{ \begin{array}{l}x = 1 – 3t\\y = – 2 + 5t\end{array} \right.\) có phương trình tham số là:
A. \(\left\{ \begin{array}{l}x = – 2 – 3t\\y = 1 + 5t\end{array} \right..\)
B. \(\left\{ \begin{array}{l}x = – 2 + 5t\\y = 1 + 3t\end{array} \right..\)
C. \(\left\{ \begin{array}{l}x = 1 – 3t\\y = 2 + 5t\end{array} \right..\)
D. \(\left\{ \begin{array}{l}x = 1 + 5t\\y = 2 + 3t\end{array} \right..\)
Câu 31: Tìm tất cả các giá trị của tham số \(m\) để khoảng cách từ điểm \(A\left( { – 1;2} \right)\) đến đường thẳng \(\Delta :mx + y – m + 4 = 0\) bằng \(2\sqrt 5 \).
A. \(m = 2.\)
B. \(\left[ \begin{array}{l}m = – 2\\m = \frac{1}{2}\end{array} \right.\).
C. \(m = – \frac{1}{2}\).
D. Không tồn tại \(m\).
Câu 32: Trong mặt phẳng \(Oxy\), đường tròn đi qua ba điểm \(A\left( {1;2} \right)\), \(B\left( {5;2} \right)\), \(C\left( {1; – 3} \right)\) có phương trình là.
A. \({x^2} + {y^2} + 25x + 19y – 49 = 0\).
B. \(2{x^2} + {y^2} – 6x + y – 3 = 0\).
C. \({x^2} + {y^2} – 6x + y – 1 = 0\).
D. \({x^2} + {y^2} – 6x + xy – 1 = 0\).
Câu 33: Trong hệ trục tọa độ \(Oxy\), cho đường tròn \(\left( C \right)\) đi qua hai điểm \(A\left( {1;\,2} \right),\,B\left( {3,\,4} \right)\) và tiếp xúc với đường thẳng \(\Delta :\,3x + y – 3 = 0\), biết tâm của \(\left( C \right)\) có tọa độ là những số nguyên. Phương trình đường tròn \(\left( C \right)\) là
A. \({x^2} + {y^2} – 3x – 7y + 12 = 0.\)
B. \({x^2} + {y^2} – 6x – 4y + 5 = 0.\)
C. \({x^2} + {y^2} – 8x – 2y + 7 = 0.\)
D. \({x^2} + {y^2} – 2x – 8y + 20 = 0.\)
Câu 34: Cho đường hypebol có phương trình \(\left( H \right):100{x^2} – 25{y^2} = 100\). Tiêu cự của hypebol đó là
A. \(2\sqrt {10} \).
B. \(2\sqrt {104} \).
C. \(\sqrt {10} \).
D. \(\sqrt {104} \).
Câu 35: Cho parabol \(\left( P \right):{y^2} = 8x\) có tiêu điểm là
A. \(F\left( {0;4} \right)\).
B. \(F\left( {0;2} \right)\).
C. \(F\left( {2;0} \right)\).
D. \(F\left( {4;0} \right)\).
Phần tự luận (3 điểm)
Bài 1. Một chiếc cổng hình parabol bao gồm một cửa chính hình chữ nhật ở giữa và hai cánh cửa phụ hai bên như hình vẽ. Biết chiều cao cổng parabol là 4m còn kích thước cửa ở giữa là 3m x 4m. Hãy tính khoảng cách giữa hai điểm A và B.

Bài 2. Cho tam giác \(ABC\) có \(A\left( {1;3} \right)\) và hai đường trung tuyến \(BM:x + 7y – 10 = 0\)và p\(CN:x – 2y + 2 = 0\). Viết phương trình đường thẳng chứa cạnh \(BC\) của tam giác \(ABC\).
Bài 3. Tìm tất cả các giá trị thực của tham số \(m\)để hàm số \(y = \frac{{mx}}{{\sqrt {x – m + 2} – 1}}\)xác định trên \(\left( {0;1} \right)\).
Bài 4. Cho tam giác \(ABC\) biết \(H\left( {3;2} \right)\), \(G\left( {\frac{5}{3};\frac{8}{3}} \right)\) lần lượt là trực tâm và trọng tâm của tam giác, đường thẳng \(BC\) có phương trình \(x + 2y – 2 = 0\). Tìm phương trình đường tròn ngoại tiếp tam giác \(ABC\)?
——– Hết ——–
Đáp án Đề thi:
Phần trắc nghiệm
|
Câu 1. C |
Câu 2. B |
Câu 3. B |
Câu 4. D |
Câu 5. A |
Câu 6. B |
Câu 7. A |
|
Câu 8. B |
Câu 9. A |
Câu 10. A |
Câu 11. C |
Câu 12. D |
Câu 13. D |
Câu 14. D |
|
Câu 15. C |
Câu 16. A |
Câu 17. A |
Câu 18. D |
Câu 19. A |
Câu 20. D |
Câu 21. B |
|
Câu 22. C |
Câu 23. B |
Câu 24. D |
Câu 25. D |
Câu 26. A |
Câu 27. D |
Câu 28. D |
|
Câu 29. A |
Câu 30. B |
Câu 31. B |
Câu 32. C |
Câu 33. C |
Câu 34. B |
Câu 35. C |
Câu 1: Tập xác định của hàm số \(y = \frac{{x + 1}}{{x – 1}}\) là:
A. \(\mathbb{R}\backslash \left\{ { \pm 1} \right\}\).
B. \(\mathbb{R}\backslash \left\{ { – 1} \right\}\).
C. \(\mathbb{R}\backslash \left\{ 1 \right\}\).
D. \(\left( {1; + \infty } \right)\).
Lời giải
Điều kiện xác định: \(x – 1 \ne 0 \Leftrightarrow x \ne 1\)
Vậy tập xác định của hàm số \(y = \frac{{x + 1}}{{x – 1}}\) là \(D = \mathbb{R}\backslash \left\{ 1 \right\}\)
Đáp án C.
Câu 2: Trong các hàm số sau, hàm số nào nghịch biến trên \(\mathbb{R}\)?
A. \(y = x\).
B. \(y = – 2x\).
C. \(y = 2x\).
D. \(y = \frac{1}{2}x\)
Lời giải
Hàm số \(y = ax + b\) với \(a \ne 0\) nghịch biến trên \(\mathbb{R}\) khi và chỉ khi \(a < 0\).
Đáp án B.
Câu 3: Cho hàm số \(f\left( x \right) = \sqrt {2{x^2} + 1} \). Giá trị \(f\left( { – 2} \right)\) bằng
A. \( – 3\).
B. \(3\).
C. \(4\).
D. Không xác định.
Lời giải
Ta có \(f\left( { – 2} \right) = \sqrt {2.{{\left( { – 2} \right)}^2} + 1} = 3\).
Đáp án B.
Câu 4: Khoảng đồng biến của hàm số \(y = {x^2} – 4x + 3\)là
A. \(\left( { – \infty ; – 2} \right)\).
B. \(\left( { – \infty ;2} \right)\).
C. \(\left( { – 2; + \infty } \right)\).
D. \(\left( {2; + \infty } \right)\).
Lời giải
Hàm số \(y = {x^2} – 4x + 3\)có \(a = 1 > 0\) nên đồng biến trên khoảng \(\left( { – \frac{b}{{2a}}; + \infty } \right)\).
Vì vậy hàm số đồng biến trên \(\left( {2; + \infty } \right)\).
Đáp án D.
Câu 5: Trục đối xứng của đồ thị hàm số \(y = a{x^2} + bx + c\), \((a \ne 0)\) là đường thẳng nào dưới đây?
A. \(x = – \frac{b}{{2a}}.\)
B. \(x = – \frac{c}{{2a}}.\)
C. \(x = – \frac{\Delta }{{4a}}.\)
D. \(x = \frac{b}{{2a}}\).
Lời giải
Đáp án A.
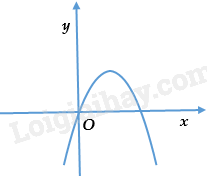
Câu 6: Cho parabol \(y = a{x^2} + bx + c\) có đồ thị như hình vẽ dưới đây. Khẳng định nào dưới đây đúng?

A. \(a > 0.\)
B. \(a < 0.\)
C. \(a = 1.\)
D. \(a = 2.\)
Lời giải
Bề lõm hướng xuống \(a < 0.\)
Đáp án B.
Câu 7: Cho \(f\left( x \right) = a{x^2} + bx + c\), \(\left( {a \ne 0} \right)\) và \(\Delta = {b^2} – 4ac\). Cho biết dấu của \(\Delta \) khi \(f\left( x \right)\) luôn cùng dấu với hệ số \(a\) với mọi \(x \in \mathbb{R}\).
A. \(\Delta < 0\).
B. \(\Delta = 0\).
C. \(\Delta > 0\).
D. \(\Delta \ge 0\).
Lời giải
Theo định lý về dấu của tam thức bậc hai thì \(f\left( x \right)\) luôn cùng dấu với hệ số \(a\) với mọi \(x \in \mathbb{R}\) khi \(\Delta < 0\).
Đáp án A.
Câu 8: Tập nghiệm \(S\) của bất phương trình \({x^2} – x – 6 \le 0\).
A. \(S = \left( { – \infty ; – 3} \right) \cup \left( {2: + \infty } \right)\).
B. \(\left[ { – 2;3} \right]\).
C. \(\left[ { – 3;2} \right]\).
D. \(\left( { – \infty ; – 3} \right] \cup \left[ {2; + \infty } \right)\).
Lời giải
Ta có: \({x^2} – x – 6 \le 0 \Leftrightarrow – 2 \le x \le 3\).
Tập nghiệm bất phương trình là: \(S = \left[ { – 2;3} \right]\).
Đáp án B.
Câu 9: Tìm tập nghiệm \(S\) của bất phương trình \({x^2} – 4x + 4 > 0\).
A. \(S = \mathbb{R}\backslash \left\{ 2 \right\}\).
B. \(S = \mathbb{R}\).
C. \(S = \left( {2; + \infty } \right)\).
D. \(S = \mathbb{R}\backslash \left\{ { – 2} \right\}\).
Lời giải
* Bảng xét dấu:
|
\(x\) |
\( – \infty \) |
\(2\) |
\( + \infty \) |
|
\({x^2} – 4x + 4\) |
\( + \) |
\(0\) |
\( + \) |
* Tập nghiệm của bất phương trình là \(S = \mathbb{R}\backslash \left\{ 2 \right\}\).
Đáp án A.
Câu 10: Phương trình \(\sqrt {x – 1} = x – 3\) có tập nghiệm là
A. \(S = \left\{ 5 \right\}\).
B. \(S = \left\{ {2;5} \right\}\).
C. \(S = \left\{ 2 \right\}\).
D. \(S = \emptyset \).
Lời giải
Ta có: \(\sqrt {x – 1} = x – 3 \Leftrightarrow \left\{ \begin{array}{l}x – 3 \ge 0\\x – 1 = {\left( {x – 3} \right)^2}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x \ge 3\\{x^2} – 7x + 10 = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x \ge 3\\\left[ \begin{array}{l}x = 2\\x = 5\end{array} \right.\end{array} \right. \Leftrightarrow x = 5\)
Vậy tập nghiệm của phương trình là: \(S = \left\{ 5 \right\}\).
Đáp án A.
Câu 11: Số nghiệm của phương trình \(\sqrt {{x^2} – 4x + 3} = \sqrt {1 – x} \)là
A. Vô số.
B. 2.
C. 1.
D. 0.
Lời giải
Ta có \(\sqrt {{x^2} – 4x + 3} = \sqrt {1 – x} \)
\( \Leftrightarrow \) \(\left\{ \begin{array}{l}1 – x \ge 0\\{x^2} – 4x + 3 = 1 – x\end{array} \right.\)\( \Leftrightarrow \)\(\left\{ \begin{array}{l}x \le 1\\{x^2} – 3x + 2 = 0\end{array} \right.\)\( \Leftrightarrow \) \(\left\{ \begin{array}{l}x \le 1\\\left[ \begin{array}{l}x = 1\\x = 2\end{array} \right.\end{array} \right.\)\( \Leftrightarrow \)\(x = 1\).
Vậy phương trình đã cho có 1 nghiệm.
Đáp án C.
Câu 12: Trong mặt phẳng \(Oxy\), đường thẳng \(\left( d \right):\,\,ax + by + c = 0,\,\,\,\left( {{a^2} + {b^2} \ne 0} \right)\). Vectơ nào sau đây là một vectơ pháp tuyến của đường thẳng \(\left( d \right)\)?
A. \(\overrightarrow n = \left( {a; – b} \right)\).
B. \(\overrightarrow n = \left( {b;a} \right)\).
C. \(\overrightarrow n = \left( {b; – a} \right)\).
D. \(\overrightarrow n = \left( {a;b} \right)\).
Lời giải
Ta có một vectơ pháp tuyến của đường thẳng \(\left( d \right)\)là \(\overrightarrow n = \left( {a;b} \right)\).
Do đó chọn đáp án
D. \(\overrightarrow {{n_1}} = \left( { – a;b} \right).\)
Đáp án D.
Câu 13: Phương trình tham số của đường thẳng đi qua hai điểm \(A\left( {2; – 1} \right)\) và \(B\left( {2;5} \right)\) là
A. \(\left\{ \begin{array}{l}x = 2t\\y = – 6t\end{array} \right.\).
B. \(\left\{ \begin{array}{l}x = 2 + t\\y = 5 + 6t\end{array} \right.\).
C. \(\left\{ \begin{array}{l}x = 1\\y = 2 + 6t\end{array} \right.\).
D. \(\left\{ \begin{array}{l}x = 2\\y = – 1 + 6t\end{array} \right.\).
Lời giải
Vectơ chỉ phương \(\overrightarrow {AB} = \left( {0;6} \right)\).
Phương trình đường thẳng \(AB\) đi qua \(A\) và có vecto chỉ phương \(\overrightarrow {AB} = \left( {0;6} \right)\) là \(\left\{ \begin{array}{l}x = 2\\y = – 1 + 6t\end{array} \right.\)
Đáp án D.
Câu 14: Trong mặt phẳng \(Oxy\), đường thẳng \(d:\,x – 2y – 1 = 0\) song song với đường thẳng có phương trình nào sau đây?
A. \(x + 2y + 1 = 0\).
B. \(2x – y = 0\).
C. \( – x + 2y + 1 = 0\).
D. \( – 2x + 4y – 1 = 0\).
Lời giải
Ta kiểm tra lần lượt các đường thẳng
.+) Với \(d{}_1:x + 2y + 1 = 0\) có \(\frac{1}{1} \ne \frac{2}{{ – 2}} \Rightarrow d\) cắt \(d{}_1\).
.+) Với \(d{}_2:2x – y = 0\) có \(\frac{2}{1} \ne \frac{{ – 1}}{{ – 2}} \Rightarrow d\)cắt \(d{}_2\).
.+) Với \(d{}_3: – x + 2y + 1 = 0\) có \(\frac{{ – 1}}{1} = \frac{2}{{ – 2}} \ne \frac{1}{{ – 1}} \Rightarrow d\)trùng \(d{}_3\).
.+) Với \(d{}_4: – 2x + 4y – 1 = 0\) có \(\frac{1}{{ – 2}} = \frac{{ – 2}}{4} \ne \frac{{ – 1}}{{ – 1}} \Rightarrow d\) song song \(d{}_4\).
Đáp án D.
Câu 15: Tính góc giữa hai đường thẳng \(\Delta :x – \sqrt 3 y + 2 = 0\) và \(\Delta ‘:x + \sqrt 3 y – 1 = 0\).
A. \({90^ \circ }\).
B. \({120^ \circ }\).
C. \({60^ \circ }\).
D. \({30^ \circ }\).
Lời giải
Đường thẳng \(\Delta \) có vectơ pháp tuyến \(\overrightarrow n = \left( {1; – \sqrt 3 } \right)\), đường thẳng \(\Delta ‘\) có vectơ pháp tuyến \(\overrightarrow {n’} = \left( {1;\sqrt 3 } \right)\).
Gọi \(\alpha \) là góc giữa hai đường thẳng \(\Delta ,\Delta ‘.\)\(\cos \alpha = \left| {\cos \left( {\overrightarrow n ,\overrightarrow {n’} } \right)} \right| = \frac{{\left| {1 – 3} \right|}}{{\sqrt {1 + 3} .\sqrt {1 + 3} }} = \frac{1}{2} \Rightarrow \alpha = {60^ \circ }\).
Đáp án C.
Câu 16: Khoảng cách từ điểm \(M\left( {5\,;\, – 1} \right)\) đến đường thẳng \(3x + 2y + 13 = 0\) là:
A. \(2\sqrt {13} \).
B. \(\frac{{28}}{{\sqrt {13} }}\).
C. \(26\).
D. \(\frac{{\sqrt {13} }}{2}\).
Lời giải
Khoảng cách \(d = \frac{{\left| {3.5 + 2.\left( { – 1} \right) + 13} \right|}}{{\sqrt {{3^2} + {2^2}} }} = \frac{{26}}{{\sqrt {13} }} = 2\sqrt {13} \).
Đáp án A.
Câu 17: Phương trình nào sau đây là phương trình đường tròn?
A. \({x^2} + {y^2} – 6x – 10y + 30 = 0\).
B. \({x^2} + {y^2} – 3x – 2y + 30 = 0\).
C. \(4{x^2} + {y^2} – 10x – 6y – 2 = 0\).
D. \({x^2} + 2{y^2} – 4x – 8y + 1 = 0\).
Lời giải
Phương trình đường tròn đã cho có dạng: \({x^2} + {y^2} – 2ax – 2by + c = 0\) là phương trình đường tròn \( \Leftrightarrow {a^2} + {b^2} – c > 0.\)
Xét đáp án A, ta có \(a = 3,\,b = 5,\,c = 30\) \( \Rightarrow {a^2} + {b^2} – c = 4 > 0\).
Đáp án A.
Câu 18: Phương trình nào sau đây là phương trình của đường tròn tâm \(I\left( { – 1;2} \right)\), bán kính bằng \(3\)?
A. \({\left( {x – 1} \right)^2} + {\left( {y + 2} \right)^2} = 9\).
B. \({\left( {x + 1} \right)^2} + {\left( {y + 2} \right)^2} = 9\).
C. \({\left( {x – 1} \right)^2} + {\left( {y – 2} \right)^2} = 9\).
D. \({\left( {x + 1} \right)^2} + {\left( {y – 2} \right)^2} = 9\).
Lời giải
Phương trình đường tròn tâm \(I\left( { – 1;2} \right)\) và bán kính \(R = 3\) là: \({\left( {x + 1} \right)^2} + {\left( {y – 2} \right)^2} = 9\).
Đáp án D.
Câu 19: Đường elip \(\frac{{{x^2}}}{9} + \frac{{{y^2}}}{7} = 1\) cắt trục tung tại hai điểm \({B_1}\), \({B_2}\). Độ dài \({B_1}{B_2}\) bằng
A. \(2\sqrt 7 \).
B. \(\sqrt 7 \).
C. \(3\).
D. \(6\).
Lời giải
Ta có \(x = 0 \Rightarrow y = \pm \sqrt 7 \).
Elip cắt trục tung tại hai điểm \({B_1}\left( {0; – \sqrt 7 } \right)\), \({B_2}\left( {0;\sqrt 7 } \right)\). Suy ra \({B_1}{B_2} = 2\sqrt 7 \).
Đáp án A.
Câu 20: Tọa độ các tiêu điểm của hypebol \(\left( H \right):\frac{{{x^2}}}{4} – \frac{{{y^2}}}{3} = 1\) là
A. \({F_1} = \left( { – 5;0} \right);{F_2} = \left( {5;0} \right)\).
B. \({F_1} = \left( {0; – 5} \right);{F_2} = \left( {0;5} \right)\).
C. \({F_1} = \left( {0; – \sqrt 7 } \right);{F_2} = \left( {0;\sqrt 7 } \right)\).
D. \({F_1} = \left( { – \sqrt 7 ;0} \right);{F_2} = \left( {\sqrt 7 ;0} \right)\).
Lời giải
Gọi \({F_1} = \left( { – c;0} \right);{F_2} = \left( {c;0} \right)\) là hai tiêu điểm của \(\left( H \right)\).
Từ phương trình \(\left( H \right):\frac{{{x^2}}}{4} – \frac{{{y^2}}}{3} = 1\), ta có: \({a^2} = 4\) và \({b^2} = 3\) suy ra \({c^2} = {a^2} + {b^2} = 7 \Rightarrow c = \sqrt 7 ,\left( {c > 0} \right)\).
Vậy tọa độ các tiêu điểm của \(\left( H \right)\)là \({F_1} = \left( { – \sqrt 7 ;0} \right);{F_2} = \left( {\sqrt 7 ;0} \right)\).
Đáp án D.
Câu 21: Tập xác định của hàm số \(y = \sqrt {4 – x} + \sqrt {x – 2} \) là
A. \(D = \left( {2;4} \right)\)
B. \(D = \left[ {2;4} \right]\)
C. \(D = \left\{ {2;4} \right\}\)
D. \(D = \left( { – \infty ;2} \right) \cup \left( {4; + \infty } \right)\)
Lời giải
Điều kiện: \(\left\{ \begin{array}{l}4 – x \ge 0\\x – 2 \ge 0\end{array} \right.\) \( \Leftrightarrow \left\{ \begin{array}{l}x \le 4\\x \ge 2\end{array} \right.\) suy ra TXĐ: \(D = \left[ {2;4} \right]\).
Đáp án B.
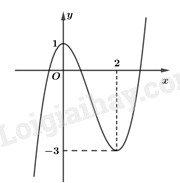
Câu 22: Cho hàm số có đồ thị như hình bên dưới.
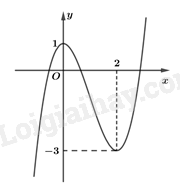
Khẳng định nào sau đây là đúng?
A. Hàm số nghịch biến trên khoảng \(\left( {0;3} \right)\).
B. Hàm số đồng biến trên khoảng \(\left( { – \infty ;1} \right)\).
C. Hàm số nghịch biến trên khoảng \(\left( {0;2} \right)\).
D. Hàm số đồng biến trên khoảng \(\left( { – \infty ;3} \right)\).
Lời giải
Trên khoảng \(\left( {0;2} \right)\), đồ thị hàm số đi xuống từ trái sang phải nên hàm số nghịch biến.
Đáp án C.
Câu 23: Đồ thị hàm số \(y = f\left( x \right) = \left\{ \begin{array}{l}2x + 3{\rm{ }}\,\,\,khi{\rm{ }}x \le 2\\{x^2} – 3{\rm{ }}\,\,\,khi{\rm{ }}x > 2\end{array} \right.\) đi qua điểm có tọa độ nào sau đây ?
A. \(\left( {0; – 3} \right)\)
B. \(\left( {3;6} \right)\)
C. \(\left( {2;5} \right)\)
D. \(\left( {2;1} \right)\)
Lời giải
Thay tọa độ điểm \(\left( {0; – 3} \right)\)vào hàm số ta được : \(f\left( 0 \right) = 3 \ne – 3\) nên loại đáp án A
Thay tọa độ điểm \(\left( {3;6} \right)\)vào hàm số ta được : \(f\left( 3 \right) = 9 – 3 = 6\), thỏa mãn nên chọn đáp án B
Đáp án B.
Câu 24: Cho parabol \(y = a{x^2} + bx + c\) có đồ thị như hình sau

Phương trình của parabol này là
A. \(y = – {x^2} + x – 1\).
B. \(y = 2{x^2} + 4x – 1\).
C. \(y = {x^2} – 2x – 1\).
D. \(y = 2{x^2} – 4x – 1\).
Lời giải
Đồ thị hàm số cắt trục tung tại điểm \(\left( {0\,\,;\,\, – 1} \right)\) nên \(c = – 1\).
Tọa độ đỉnh \(I\left( {1\,\,;\, – 3} \right)\), ta có phương trình: \(\left\{ \begin{array}{l} – \frac{b}{{2a}} = 1\\a{.1^2} + b.1 – 1 = – 3\end{array} \right.\) \( \Leftrightarrow \left\{ \begin{array}{l}2a + b = 0\\a + b = – 2\end{array} \right.\) \( \Leftrightarrow \left\{ \begin{array}{l}a = 2\\b = – 4\end{array} \right.\).
Vậy parabol cần tìm là: \(y = 2{x^2} – 4x – 1\).
Đáp án D.
Câu 25: Tọa độ giao điểm của \(\left( P \right)\,:\,y = {x^2} – 4x\) với đường thẳng \(d\,:\,y = – x – 2\) là
A. \(M\left( {0;\, – 2} \right)\), \(N\left( {2;\, – 4} \right)\).
B. \(M\left( { – 1;\, – 1} \right)\), \(N\left( { – 2;\,0} \right)\).
C. \(M\left( {\, – 3;\,1} \right)\), \(N\left( {3;\, – 5} \right)\).
D. \(M\left( {1;\, – 3} \right)\), \(N\left( {2;\, – 4} \right)\).
Lời giải
Hoành độ giao điểm của \(\left( P \right)\) và \(d\) là nghiệm của phương trình:
\({x^2} – 4x = – x – 2\, \Leftrightarrow \,{x^2} – 3x + 2 = 0\, \Leftrightarrow \,\left[ \begin{array}{l}x = 1\\x = 2\end{array} \right.\).
Vậy tọa độ giao điểm của \(\left( P \right)\) và \(d\) là \(M\left( {1;\, – 3} \right)\), \(N\left( {2;\, – 4} \right)\).
Đáp án D.
Câu 26: Số nghiệm nguyên của bất phương trình \(2{x^2} – 3x – 15 \le 0\) là
A. \(6\).
B. \(5\).
C. \(8\).
D. \(7\).
Lời giải
Xét \(f\left( x \right) = 2{x^2} – 3x – 15\).
\(f\left( x \right) = 0\)\( \Leftrightarrow x = \frac{{3 \pm \sqrt {129} }}{4}\).
Ta có bảng xét dấu:

Tập nghiệm của bất phương trình là \(S = \left[ {\frac{{3 – \sqrt {129} }}{4};\,\frac{{3 + \sqrt {129} }}{4}} \right]\).
Do đó bất phương trình có \(6\) nghiệm nguyên là \( – 2\), \( – 1\), \(0\), \(1\), \(2\), \(3\).
Đáp án A.
Câu 27: Tìm tất cả các giá trị của tham số \(m\) để bất phương trình \({x^2} – \left( {m + 2} \right)x + 8m + 1 \le 0\) vô nghiệm.
A. \(m \in \left[ {0;28} \right]\).
B. \(m \in \left( { – \infty ;0} \right) \cup \left( {28; + \infty } \right)\).
C. \(m \in \left( { – \infty ;0} \right] \cup \left[ {28; + \infty } \right)\).
D. \(m \in \left( {0;28} \right)\).
Lời giải
Bất phương trình vô nghiệm khi và chỉ khi \({\left( {m + 2} \right)^2} – 4\left( {8m + 1} \right) < 0\)\( \Leftrightarrow {m^2} – 28m < 0\) \(0 < m < 28\)
Đáp án D.
Câu 28: Số nghiệm của phương trình \(\sqrt {{x^2} – 3x + 1} = 4x – 1\) là
A. \(0\).
B. \(3\).
C. \(2\).
D. \(1\).
Lời giải
Phương trình \(\sqrt {{x^2} – 3x + 1} = 4x – 1\)\( \Leftrightarrow \left\{ \begin{array}{l}4x – 1 \ge 0\\{x^2} – 3x + 1 = {\left( {4x – 1} \right)^2}\end{array} \right.\)
\( \Leftrightarrow \left\{ \begin{array}{l}x \ge \frac{1}{4}\\15{x^2} – 5x = 0\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}x \ge \frac{1}{4}\\\left[ \begin{array}{l}x = 0\left( l \right)\\x = \frac{1}{3}\left( n \right)\end{array} \right.\end{array} \right.\)\( \Leftrightarrow x = \frac{1}{3}\).
Đáp án B.
Câu 29: Cho đường thẳng \(d\) có phương trình tham số \(\left\{ \begin{array}{l}x = 5 + t\\y = – 9 – 2t\end{array} \right.\). Phương trình tổng quát của đường thẳng \(d\) là
A. \(2x + y – 1 = 0\).
B. \( – 2x + y – 1 = 0\).
C. \(x + 2y + 1 = 0\).
D. \(2x + 3y – 1 = 0\).
Lời giải
Đường thẳng \(\left( d \right):\left\{ \begin{array}{l}x = 5 + t\\y = – 9 – 2t\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}t = x – 5\\y = – 9 – 2t\end{array} \right.\)\( \Rightarrow y = – 9 – 2\left( {x – 5} \right)\)\( \Leftrightarrow 2x + y – 1 = 0\).
Đáp án A.
Câu 30: Đường thẳng \(d\) đi qua điểm \(M\left( { – 2;1} \right)\) và vuông góc với đường thẳng \(\Delta :\left\{ \begin{array}{l}x = 1 – 3t\\y = – 2 + 5t\end{array} \right.\) có phương trình tham số là:
A. \(\left\{ \begin{array}{l}x = – 2 – 3t\\y = 1 + 5t\end{array} \right..\)
B. \(\left\{ \begin{array}{l}x = – 2 + 5t\\y = 1 + 3t\end{array} \right..\)
C. \(\left\{ \begin{array}{l}x = 1 – 3t\\y = 2 + 5t\end{array} \right..\)
D. \(\left\{ \begin{array}{l}x = 1 + 5t\\y = 2 + 3t\end{array} \right..\)
Lời giải
\(\left\{ \begin{array}{l}M\left( { – 2;1} \right) \in d\\{{\vec u}_\Delta } = \left( { – 3;5} \right)\\d \bot \Delta \end{array} \right. \to \left\{ \begin{array}{l}M\left( { – 2;1} \right) \in d\\{{\vec n}_d} = \left( { – 3;5} \right) \to {{\vec u}_d} = \left( {5;3} \right)\end{array} \right. \to d:\left\{ \begin{array}{l}x = – 2 + 5t\\y = 1 + 3t\end{array} \right.\left( {t \in \mathbb{R}} \right).\)
Đáp án B.
Câu 31: Tìm tất cả các giá trị của tham số \(m\) để khoảng cách từ điểm \(A\left( { – 1;2} \right)\) đến đường thẳng \(\Delta :mx + y – m + 4 = 0\) bằng \(2\sqrt 5 \).
A. \(m = 2.\)
B. \(\left[ \begin{array}{l}m = – 2\\m = \frac{1}{2}\end{array} \right.\).
C. \(m = – \frac{1}{2}\).
D. Không tồn tại \(m\).
Lời giải
\(d\left( {A;\Delta } \right) = \frac{{\left| { – m + 2 – m + 4} \right|}}{{\sqrt {{m^2} + 1} }} = 2\sqrt 5 \Leftrightarrow \left| {m – 3} \right| = \sqrt 5 .\sqrt {{m^2} + 1} \Leftrightarrow 4{m^2} + 6m – 4 = 0\)
\( \Leftrightarrow \left[ \begin{array}{l}m = – 2\\m = \frac{1}{2}\end{array} \right..\)
Đáp án B.
Câu 32: Trong mặt phẳng \(Oxy\), đường tròn đi qua ba điểm \(A\left( {1;2} \right)\), \(B\left( {5;2} \right)\), \(C\left( {1; – 3} \right)\) có phương trình là.
A. \({x^2} + {y^2} + 25x + 19y – 49 = 0\).
B. \(2{x^2} + {y^2} – 6x + y – 3 = 0\).
C. \({x^2} + {y^2} – 6x + y – 1 = 0\).
D. \({x^2} + {y^2} – 6x + xy – 1 = 0\).
Lời giải
Gọi \(\left( C \right)\) là phương trình đường tròn đi qua ba điểm \(A,B,C\) với tâm \(I\left( {a;b} \right)\)
\( \Rightarrow \left( C \right)\)có dạng: \({x^2} + {y^2} – 2ax – 2by + c = 0\). Vì đường tròn \(\left( C \right)\) đi qua qua ba điểm \(A,B,C\) nên ta có hệ phương trình:
\(\left\{ \begin{array}{l}1 + 4 – 2a – 4b + c = 0\\25 + 4 – 10a – 4b + c = 0\\1 + 9 – 2a + 6b + c = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l} – 2a – 4b + c = – 5\\ – 10a – 4b + c = – 29\\ – 2a + 6b + c = – 10\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = 3\\b = – \frac{1}{2}\\c = – 1\end{array} \right.\).
Vậy phương trình đường tròn cần tìm là \({x^2} + {y^2} – 6x + y – 1 = 0\).
Đáp án C.
Câu 33: Trong hệ trục tọa độ \(Oxy\), cho đường tròn \(\left( C \right)\) đi qua hai điểm \(A\left( {1;\,2} \right),\,B\left( {3,\,4} \right)\) và tiếp xúc với đường thẳng \(\Delta :\,3x + y – 3 = 0\), biết tâm của \(\left( C \right)\) có tọa độ là những số nguyên. Phương trình đường tròn \(\left( C \right)\) là
A. \({x^2} + {y^2} – 3x – 7y + 12 = 0.\)
B. \({x^2} + {y^2} – 6x – 4y + 5 = 0.\)
C. \({x^2} + {y^2} – 8x – 2y + 7 = 0.\)
D. \({x^2} + {y^2} – 2x – 8y + 20 = 0.\)
Lời giải
Ta có : \(\overrightarrow {AB} = (2;2)\) ; đoạn \(AB\) có trung điểm \(M\left( {2;\,3} \right)\)
\( \Rightarrow \)Phương trình đường trung trực của đoạn \(AB\) là \(d:\,x + y – 5 = 0\).
Gọi \(I\) là tâm của \(\left( C \right)\) \( \Rightarrow I \in d\)\( \Rightarrow I\left( {a;\,5 – a} \right)\,,\,a \in \mathbb{Z}.\)
Ta có: \(R = IA = d\left( {I;\,\Delta } \right) = \sqrt {{{\left( {a – 1} \right)}^2} + {{\left( {a – 3} \right)}^2}} = \frac{{\left| {2a + 2} \right|}}{{\sqrt {10} }} \Leftrightarrow a = 4 \Rightarrow I\left( {4;\,1} \right),\,R = \sqrt {10} .\)
Vậy phương trình đường tròn là: \({\left( {x – 4} \right)^2} + {\left( {y – 1} \right)^2} = 10 \Leftrightarrow {x^2} + {y^2} – 8x – 2y + 7 = 0.\)
Đáp án C.
Câu 34: Cho đường hypebol có phương trình \(\left( H \right):100{x^2} – 25{y^2} = 100\). Tiêu cự của hypebol đó là
A. \(2\sqrt {10} \).
B. \(2\sqrt {104} \).
C. \(\sqrt {10} \).
D. \(\sqrt {104} \).
Lời giải
\(\left( H \right):100{x^2} – 25{y^2} = 100 \Leftrightarrow \frac{{{x^2}}}{{100}} – \frac{{{y^2}}}{4} = 1\).
\(a = 10,b = 2 \Rightarrow c = \sqrt {{a^2} + {b^2}} = \sqrt {104} \).
Tiêu cự của hypebol là \(2\sqrt {104} \).
Đáp án B.
Câu 35: Cho parabol \(\left( P \right):{y^2} = 8x\) có tiêu điểm là
A. \(F\left( {0;4} \right)\).
B. \(F\left( {0;2} \right)\).
C. \(F\left( {2;0} \right)\).
D. \(F\left( {4;0} \right)\).
Lời giải
Ta có \(2p = 8 \Rightarrow p = 4\).
Parabol có tiêu điểm \(F\left( {2;0} \right)\).
Đáp án C.
Phần tự luận (3 điểm)
Bài 1. Một chiếc cổng hình parabol bao gồm một cửa chính hình chữ nhật ở giữa và hai cánh cửa phụ hai bên như hình vẽ. Biết chiều cao cổng parabol là 4m còn kích thước cửa ở giữa là 3m x 4m. Hãy tính khoảng cách giữa hai điểm A và B.

Lời giải

Gắn hệ trục tọa độ Oxy như hình vẽ, chiếc cổng là 1 phần của parabol \(\left( P \right):y = a{x^2} + bx + c\) với \(a < 0\).
Do parabol \((P)\) đối xứng qua trục tung nên có trục đối xứng \(x = 0 \Rightarrow – \frac{b}{{2a}} = 0 \Leftrightarrow b = 0\) .
Chiều cao của cổng parabol là 4m nên \(G\left( {0;4} \right) \Rightarrow c = 4\)
\( \Rightarrow \left( P \right):y = a{x^2} + 4\).
Lại có, kích thước cửa ở giữa là 3m x 4m nên \(E\left( {2;3} \right) \Rightarrow 3 = 4a + 4 \Rightarrow a = – \frac{1}{4}\) .
Vậy \(\left( P \right):y = – \frac{1}{4}{x^2} + 4\).
Ta có \( – \frac{1}{4}{x^2} + 4 = 0 \Leftrightarrow \left[ \begin{array}{l}x = 4\\x = – 4\end{array} \right.\) nên \(A\left( { – 4;0} \right);B\left( {4;0} \right)\) hay \(AB = 8\).
Bài 2. Cho tam giác \(ABC\) có \(A\left( {1;3} \right)\) và hai đường trung tuyến \(BM:x + 7y – 10 = 0\) và \(CN:x – 2y + 2 = 0\). Viết phương trình đường thẳng chứa cạnh \(BC\) của tam giác \(ABC\).
Lời giải

Vì \(B \in BM\) nên tọa độ điểm \(B\) có dạng \(B\left( { – 7b + 10;\,b} \right)\).
Gọi \(G\) là trọng tâm của tam giác \(ABC\).
Khi đó tọa độ điểm \(G\) là nghiệm của hệ phương trình
\(\left\{ \begin{array}{l}x + 7y – 10 = 0\\x – 2y + 2 = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = \frac{2}{3}\\y = \frac{4}{3}\end{array} \right. \Rightarrow G\left( {\frac{2}{3};\,\frac{4}{3}} \right)\).
Gọi \(P\left( {x;\,y} \right)\) là trung điểm của \(BC\).
Khi đó \(AP\) là đường trung tuyến của tam giác \(ABC\).
Suy ra \(\overrightarrow {AG} = \frac{2}{3}\overrightarrow {AP} \Leftrightarrow \left\{ \begin{array}{l}\frac{2}{3} – 1 = \frac{2}{3}\left( {x – 1} \right)\\\frac{4}{3} – 3 = \frac{2}{3}\left( {y – 3} \right)\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = \frac{1}{2}\\y = \frac{1}{2}\end{array} \right. \Rightarrow P\left( {\frac{1}{2};\,\frac{1}{2}} \right)\).
Vì \(P\) là trung điểm của \(BC\) nên \(\left\{ \begin{array}{l}{x_C} = 2{x_P} – {x_B}\\{y_C} = 2{y_P} – {y_B}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{x_C} = 7b – 9\\{y_C} = 1 – b\end{array} \right.\) \( \Rightarrow C\left( {7b – 9;\,1 – b} \right)\).
Vì \(C \in CN\) nên \(7b – 9 – 2.\left( {1 – b} \right) + 2 = 0 \Leftrightarrow b = 1\).
Khi đó \(B\left( {3;\,1} \right)\), \(C\left( { – 2;\,0} \right)\).
Vậy phương trình đường thẳng \(BC\) đi qua hai điểm \(B\) và \(C\) là \(x – 5y + 2 = 0\).
Bài 3. Tìm tất cả các giá trị thực của tham số \(m\)để hàm số \(y = \frac{{mx}}{{\sqrt {x – m + 2} – 1}}\)xác định trên \(\left( {0;1} \right)\).
Lời giải
Hàm số xác định trên \(\left( {0;1} \right) \Leftrightarrow \left\{ \begin{array}{l}x – m + 2 \ge 0\\\sqrt {x – m + 2} – 1 \ne 0\end{array} \right.\forall x \in \left( {0;1} \right)\)
\( \Leftrightarrow \left\{ \begin{array}{l}x \ge m – 2\\\sqrt {x – m + 2} \ne 1\end{array} \right.\forall x \in \left( {0;1} \right) \Leftrightarrow \left\{ \begin{array}{l}x \ge m – 2\\x \ne m – 1\end{array} \right.\forall x \in \left( {0;1} \right)\) \( \Leftrightarrow \left\{ \begin{array}{l}m – 2 \le 0\\\left[ \begin{array}{l}m – 1 \ge 1\\m – 1 \le 0\end{array} \right.\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}m \le 2\\\left[ \begin{array}{l}m \ge 2\\m \le 1\end{array} \right.\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}m \le 1\\m = 2\end{array} \right.\)
Vậy \(m \in \left( { – \infty ;1} \right] \cup \left\{ 2 \right\}\).
Bài 4. Cho tam giác \(ABC\) biết \(H\left( {3;2} \right)\), \(G\left( {\frac{5}{3};\frac{8}{3}} \right)\) lần lượt là trực tâm và trọng tâm của tam giác, đường thẳng \(BC\) có phương trình \(x + 2y – 2 = 0\). Tìm phương trình đường tròn ngoại tiếp tam giác \(ABC\)?
Lời giải

*) Gọi \(I\) là tâm đường tròn ngoại tiếp tam giác \(ABC\).
\( \Rightarrow \overrightarrow {HI} = \frac{3}{2}\overrightarrow {HG} \)\( \Rightarrow \left\{ \begin{array}{l}{x_I} – 3 = \frac{3}{2}\left( {\frac{5}{3} – 3} \right)\\{y_I} – 2 = \frac{3}{2}\left( {\frac{8}{3} – 2} \right)\end{array} \right.\) \( \Rightarrow \left\{ \begin{array}{l}{x_I} = 1\\{y_I} = 3\end{array} \right.\)
*) Gọi \(M\) là trung điểm của \(BC\) \( \Rightarrow IM \bot BC\) \( \Rightarrow IM:2x – y + 1 = 0\).
\(M = IM \cap BC\) \( \Rightarrow \left\{ \begin{array}{l}2x – y = – 1\\x + 2y = 2\end{array} \right.\)\( \Rightarrow \left\{ \begin{array}{l}x = 0\\y = 1\end{array} \right.\)\( \Rightarrow M\left( {0;1} \right)\).
Lại có: \(\overrightarrow {MA} = 3\overrightarrow {MG} \) \( \Rightarrow \left\{ \begin{array}{l}{x_A} = 3.\frac{5}{3}\\{y_A} – 1 = 3.\left( {\frac{8}{3} – 1} \right)\end{array} \right.\) \( \Rightarrow \left\{ \begin{array}{l}{x_A} = 5\\{y_A} = 6\end{array} \right.\).
Suy ra: bán kính đường tròn ngoại tiếp tam giác \(ABC\) là \(R = IA = 5\).
Vậy phương trình đường tròn ngoại tiếp tam giác \(ABC\) là \({\left( {x – 1} \right)^2} + {\left( {y – 3} \right)^2} = 25\).