Vận dụng kiến thức giải Đề kiểm tra học kì 2 Toán 10 – Đề số 3 – Kết nối tri thức – Đề thi học kì 2 – Đề thi đề kiểm tra Toán lớp 10 Kết nối tri thức. I. PHẦN TRẮC NGHIỆM ( 35 câu – 7,0 điểm )….
Đề thi:
I. PHẦN TRẮC NGHIỆM (35 câu – 7,0 điểm).
Câu 1: Cho hàm số \(y = f\left( x \right)\) có tập xác định là \(\left[ { – 3;\,3} \right]\) và đồ thị của nó được biểu diễn bởi hình vẽ bên.
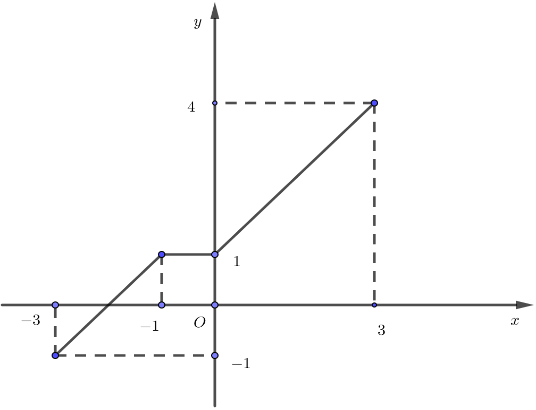
Khẳng định nào sau đây là đúng?
A. Hàm số đồng biến trên khoảng \(\left( { – 3;\,3} \right)\).
B. Hàm số đồng biến trên khoảng \(\left( { – 3;\, – 1} \right)\) và \(\left( {1;\,3} \right)\).
C. Hàm số đồng biến trên khoảng \(\left( { – 3;\, – 1} \right)\) và \(\left( {1;\,4} \right)\).
D. Hàm số nghịch biến trên khoảng \(\left( { – 1;\,0} \right)\).
Câu 2: Tập xác định của hàm số \(y = \sqrt {2 – x} + \frac{x}{{\sqrt {7 + x} }}\) là
A. \(\left[ {2; + \infty } \right)\).
B. \(\left( { – 7;2} \right]\).
C. \(\mathbb{R}\backslash \left\{ { – 7;2} \right\}\).
D. \(\left( { – 7;2} \right)\)
Câu 3: Cho hàm số bậc hai \(y = a{x^2} + bx + c\) \(y = a{x^2} + bx + c\) có đồ thị \(y = a{x^2} + bx + c\), đỉnh của \(y = a{x^2} + bx + c\) được xác định bởi công thức nào?
A. \(y = a{x^2} + bx + c\).
B. \(y = a{x^2} + bx + c\).
C. \(y = a{x^2} + bx + c\).
D. \(y = a{x^2} + bx + c\).
Câu 4: Đồ thị dưới đây là của hàm số nào?
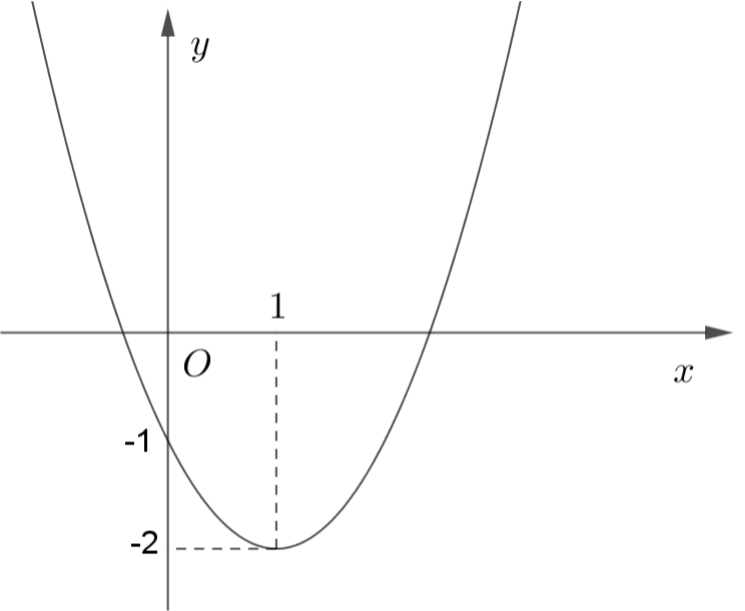
A. \(y = {x^2} + x – 4\).
B. \(y = {x^2} – 2x – 1\).
C. \(y = – {x^2} – 2x + 1\).
D. \(y = 2x – 4\).
Câu 5: Cho tam thức \(f(x) = a{x^2} + bx + c\,(a > 0),\,\,\Delta = {b^2} – 4ac\). Mệnh đề nào sau đây đúng?
A. \(f(x) \ge 0\,\)với mọi x thuộc \({\rm{R}}\) khi \(\Delta > 0\).
B. \(f(x) < 0\,\)với mọi x thuộc \({\rm{R}}\) khi \(\Delta < 0\).
C. \(f(x) < 0\,\)với mọi x thuộc \({\rm{R}}\) khi \(\Delta = 0\).
D. \(f(x) > 0\,\)với mọi x thuộc \({\rm{R}}\) khi \(\Delta < 0\).
Câu 6: Tập nghiệm của bất phương trình \( – {x^2} + 3x \le 0\) là
A. \(\left( { – \infty \,;\,0} \right) \cup \left( {3\,;\, + \infty } \right)\).
B. \(\left( { – \infty \,;\,0} \right] \cup \left[ {3\,;\, + \infty } \right)\).
C. \(\left( {0\,;\,3} \right)\).
D. \(\left[ {0\,;\,3} \right]\).
Câu 7: Giá trị \(x = 2\)là nghiệm của phương trình nào sau đây?
A. \(\sqrt {{x^2} – x – 4} = \sqrt {x – 4} \).
B. \(x – 2 = \sqrt {x – 3} \).
C. \(x + 2 = 2\sqrt {3x – 2} \).
D. \(x + 2 = \sqrt {x + 1} \).
Câu 8: Tập nghiệm \(S\) của phương trình \(\sqrt {2x – 3} = x – 3\) là:
A. \(S = \left\{ 6 \right\}.\)
B. \(S = \emptyset .\)
C. \(S = \left\{ {6;2} \right\}.\)
D. \(S = \left\{ 2 \right\}.\)
Câu 9: Trong mặt phẳng với hệ trục tọa độ \(Oxy\), cho đường thẳng \(d:2x – 3y + 1 = 0\). Vectơ nào dưới đây là vectơ pháp tuyến của đường thẳng \(d\)?
A. \(\overrightarrow {{n_2}} = (2;3)\).
B. \(\overrightarrow {{n_3}} = (3;2)\).
C. \(\overrightarrow {{n_1}} = (2; – 3)\).
D. \(\overrightarrow {{n_4}} = ( – 3;2)\).
Câu 10: Phuong trình tổng quát đường thẳng đi qua A(1; 3) có vectơ pháp tuyến có dạng:
A. \(2x – 3y + 3 = 0\)
B. \(3x – 2y + 1 = 0\)
C. \(3x – 2y + 3 = 0\)
D. \(2x + 3y – 1 = 0\)
Câu 11: Cho 2 điểm \(A\left( {1; – 4} \right)\),\(B\left( {1;{\rm{ }}2} \right)\). Viết phương trình tổng quát đường trung trực của đoạn thẳng \(AB\).
A. \(y – 1 = 0\). B. \(x – 4y = 0\). C. \(x – 1 = 0\). D. \(y + 1 = 0\).
Câu 12: Khoảng cách từ \(I(1; – 2)\) đến đường thẳng \(\Delta :3x – 4y – 26 = 0\) bằng
A. 3. B. \(12\). C. 5. D. \(\frac{5}{3}\).
Câu 13: Cho \(\Delta :x – 3y + 1 = 0\)và .\(d:3x – y – 1 = 0\) Vị trí của và d là:
A. Song song với nhau.
B. Trùng nhau
C. Vuông góc với nhau.
D. Cắt nhau nhưng không vuông góc với nhau.
Câu 14: Góc giữa hai đường thẳng \(a:\,\sqrt 3 x – y + 7 = 0\) và \(b:x – \sqrt 3 y – 1 = 0\)là:
A. \(30^\circ \).
B. \(90^\circ \).
C. \(60^\circ \).
D. \(45^\circ \).
Câu 15: Trong mặt phẳng tọa độ \(Oxy\), phương trình nào sau đây là phương trình của đường tròn?
A. \({x^2} + 2{y^2} – x + 8y + 1 = 0\).
B. \({x^2} + {y^2} + 4x + 6y – 12 = 0\).
C. \({x^2} + {y^2} – 2x – 8y + 25 = 0\).
D. \(4{x^2} – 4{y^2} + 9x – 6y – 1 = 0\).
Câu 16: Xác định tâm và bán kính của đường tròn \(\left( C \right):{\left( {x + 1} \right)^2} + {\left( {y – 2} \right)^2} = 9.\)
A. Tâm \(I\left( { – 1;2} \right),\) bán kính \(R = 3\).
B. Tâm \(I\left( { – 1;2} \right),\) bán kính \(R = 9\).
C. Tâm \(I\left( {1; – 2} \right),\) bán kính \(R = 3\).
D. Tâm \(I\left( {1; – 2} \right),\) bán kính \(R = 9\).
Câu 17: Cho phương trình \({x^2} + {y^2} – 2mx – 4\left( {m – 2} \right)y + 6 – m = 0\,(1)\). Điều kiện của \(m\)để \((1)\)là phương trình của đường tròn.
A. \(m = 2\).
B. \(\left[ \begin{array}{l}m 2\end{array} \right.\).
C. \(1 < m < 2\).
D. \(\left[ \begin{array}{l}m = 1\\m = 2\end{array} \right.\).
Câu 18: Trong mặt phẳng với hệ trục tọa độ \(Oxy\), cho đường tròn\((C)\) có tâm \(I(1; – 2)\) và bán kính \(R = 3\). Viết phương trình của đường tròn (C).
A. \({(x + 1)^2} + {(y – 2)^2} = 9\).
B. \({(x – 1)^2} + {(y + 2)^2} = 3\).
C. \({(x – 1)^2} – {(y + 2)^2} = 9\).
D. \({(x – 1)^2} + {(y + 2)^2} = 9\).
Câu 19: Parbol \(5{y^2} = 12x\)có tiêu điểm là:
A. \(\left( {\frac{3}{5};0} \right)\).
B. \(\left( {\frac{6}{5};0} \right)\).
C. \(\left( {\frac{{12}}{5};0} \right)\).
D. \(\left( {\frac{3}{{10}};0} \right)\).
Câu 20: Phương trình chính tắc của e líp có độ dài trục lớn bằng , trục nhỏ bằng là:
A. \(\frac{{{x^2}}}{{64}} + \frac{{{y^2}}}{{36}} = 1\).
B. \(\frac{{{x^2}}}{{16}} – \frac{{{y^2}}}{9} = 1\).
C. \(\frac{{{x^2}}}{9} + \frac{{{y^2}}}{{16}} = 1\).
D. \(\frac{{{x^2}}}{{16}} + \frac{{{y^2}}}{9} = 1\).
Câu 21: Bình có 4 cây bút chì khác nhau và 5 cây bút mực khác nhau. Bình cần chọn một cây bút để tặng bạn, hỏi Bình có bao nhiêu cách chọn?
A. \(5.\) B. \(4.\) C. \(9.\) D. \(20.\)
Câu 22: Một người vào cửa hàng ăn, người đó chọn thực đơn gồm \(1\) món ăn trong \(5\) món, \(1\) loại quả tráng miệng trong \(5\) loại quả tráng miệng và một nước uống trong \(3\) loại nước uống. Có bao nhiêu cách chọn thực đơn.
A. \(25\). B. \(75\). C. \(100\). D. \(15\).
Câu 23: Từ các số \(1,2,3\) có thể lập được bao nhiêu số tự nhiên khác nhau và mỗi số có các chữ số khác nhau:
A. \(36\) B. \(20\). C. \(72\). D. \(15\).
Câu 24: Cho hai số tự nhiên \(k,\,\,n\) thỏa \(1 \le k \le n\). Mệnh đề nào sau đây đúng?
A. \(A_n^k = \frac{{n!}}{{k!(n – k)!}}.\)
B. \(A_n^k = \frac{{k!(n – k)!}}{{n!}}.\)
C. \(A_n^k = \frac{{n!}}{{\left( {n – k} \right)!}}.\)
D. \(A_n^k = \frac{{(n – k)!}}{{n!}}.\)
Câu 25: Có bao nhiêu cách xếp 6 bạn thành một hàng dọc?
A. \({6^6}\). B. \(5!\). C. \(6\). D. \(6!\).
Câu 26: Tổ 1 của lớp 10A có 10 học sinh gồm 6 nam và 4 nữ. Cô giáo chủ nhiệm chọn 7 em đi lao động, trong đó có 4 nam và 3 nữ. Hỏi cô giáo chủ nhiệm có tất cả bao nhiêu cách chọn?
A. \(19.\) B. \(120.\) C. \(8640.\) D. \(60.\)
Câu 27: Có 5 quyển sách khác nhau gồm 3 quyển sách Văn và 2 quyển sách Toán. Hỏi có bao nhiêu cách xếp 5 quyển sách trên lên kệ sách dài (xếp hàng ngang) sao cho tất cả quyển sách cùng môn phải đứng cạnh nhau?
A. 12 cách. B. 24 cách. C. 120 cách. D. 16 cách.
Câu 28: Cho hai đường thẳng song song \(a\) và \(b\). Trên đường thẳng \(a\) có 5 điểm phân biệt, trên đường thẳng \(b\) có 7 điểm phân biệt. Tính số tam giác có 3 đỉnh lấy từ các điểm trên hai đường thẳng \(a\) và \(b\).
A. 175 tam giác. B. 220 tam giác. C. 45 tam giác. D. 350 tam giác.
Câu 29: Khai triển nhị thức \({\left( {2x + y} \right)^5}\). Ta được kết quả là
A. \(32{x^5} + 16{x^4}y + 8{x^3}{y^2} + 4{x^2}{y^3} + 2x{y^4} + {y^5}\).
B. \(32{x^5} + 80{x^4}y + 80{x^3}{y^2} + 40{x^2}{y^3} + 10x{y^4} + {y^5}\).
C. \(2{x^5} + 10{x^4}y + 20{x^3}{y^2} + 20{x^2}{y^3} + 10x{y^4} + {y^5}\).
D. \(32{x^5} + 10000{x^4}y + 80000{x^3}{y^2} + 400{x^2}{y^3} + 10x{y^4} + {y^5}\).
Câu 30: Gieo 3 đồng tiền là một phép thử ngẫu nhiên có không gian mẫu là:
A. {NN, NS, SN, SS}
B. .{NNN, SSS, NNS, SSN, NSN, SNS}
C. .{NNN, SSS, NNS, SSN, NSN, SNS, NSS,SNN}
D. .{NNN, SSS, NNS, SSN, NSS, SNN}
Câu 31: Cho A là một biến cố liên quan phép thử T. Mệnh đề nào sau đây là mệnh đề đúng?
A. là số lớn hơn 0.
B. \(0 \le P(A) \le 1\).
C. .\(P(A) = 0 \Leftrightarrow A = \Omega \)
D. là số nhỏ hơn 1.
Câu 32: Gieo một đồng tiền liên tiếp lần. Số phần tử của không gian mẫu là?
A. 1. B. 2. C. 4. D. 8.
Câu 33: Gieo một con súc sắc. Xác suất để mặt chấm chẵn xuất hiện là:
A. 0,2 B. 0,3. C. 0,4 D. 0,5.
Câu 34: Một hộp đựng bi xanh và bi đỏ, lần lượt rút viên bi. Xác suất để rút được một bi xanh và 1 bi đỏ là:
A. \(\frac{2}{{15}}\)
B.\(\frac{6}{{25}}\)
C. \(\frac{8}{{25}}\).
D. \(\frac{4}{{15}}\).
Câu 35: Có hai hộp bi, hộp thứ nhất có 4 bi đỏ và 3 bi trắng, hộp thứ hai có 2 bi đỏ và 4 bi trắng. Chọn ngẫu nhiên mỗi hộp ra 1 viên bi. Tính xác suất \(P\) để chọn được hai viên bi cùng màu.
A. \(P = \frac{8}{{21}}\).
B. \(P = \frac{3}{7}\).
C. \(P = \frac{{10}}{{21}}\).
D. \(P = \frac{4}{9}\).
II. TỰ LUẬN (04 câu – 3,0 điểm)
Câu 37: Tìm \(m\) để bất phương trình \({x^2} – 2\left( {m + 1} \right)x + 2{m^2} – 5m + 11 < 0\) vô nghiệm.
Câu 38: Khi du lịch đến thành phố St. Louis (Mỹ), ta sẽ thấy một cái cổng lớn có hình parabol hướng bề lõm xuống dưới, đó là cổng Arch. Giả sử ta lập một hệ toạ độ Oxy sao cho một chân cổng đi qua gốc O như Hình 16 (x và y tính bằng mét), chân kia của cổng ở vị trí có tọa độ ( 163,0) . Biết một điểm M trên cổng có toạ độ là (10,43).

Tính chiều cao của cổng (tính từ điểm cao nhất trên cổng xuống mặt đất), làm tròn kết quả đến hàng đơn vị.
Câu 39: Trong mặt phẳng với hệ trục tọa độ Oxy, cho hai điểm \(A(2;0)\), \(B( – 2;2)\) và đường thẳng \(d:3x + 4y + 11 = 0\).
a. Viết phương trình chính tắc của Elip (E), biết (E) có độ dài trục lớn bằng 6 và có một tiêu điểm là A.
b. Gọi (C) là đường tròn đường kính AB; tìm điểm M trên đường thẳng d sao cho qua M vẽ được
hai tiếp tuyến MP, MQ đến (C) (P,Q là hai tiếp điểm) mà đoạn thẳng PQ có độ dài nhỏ nhất.
———- HẾT ———-
Đáp án Đề thi:
HƯỚNG DẪN GIẢI CHI TIẾT
THỰC HIỆN: BAN CHYÊN MÔN GiaiBaitapsgk.COM
I. PHẦN TRẮC NGHIỆM (35 câu – 7,0 điểm).

Câu 1: Cho hàm số \(y = f\left( x \right)\) có tập xác định là \(\left[ { – 3;\,3} \right]\) và đồ thị của nó dược biểu diễn bởi hình vẽ bên.
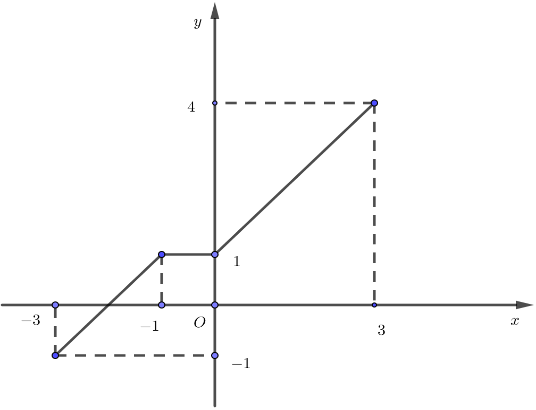
Khẳng định nào sau đây là đúng?
A. Hàm số đồng biến trên khoảng \(\left( { – 3;\,3} \right)\).
B. Hàm số đồng biến trên khoảng \(\left( { – 3;\, – 1} \right)\) và \(\left( {1;\,3} \right)\).
C. Hàm số đồng biến trên khoảng \(\left( { – 3;\, – 1} \right)\) và \(\left( {1;\,4} \right)\).
D. Hàm số nghịch biến trên khoảng \(\left( { – 1;\,0} \right)\).
Phương pháp
– Hàm số có chiều đi lên từ trái sang phải là đồng biến.
– Hàm số có chiều đi xuống từ trái sang phải là nghịch biến.
Lời giải
Chọn B
Quan sát đồ thị ta thấy hàm số đồng biến trên khoảng \(\left( { – 3;\, – 1} \right)\) và \(\left( {1;\,3} \right)\).
Câu 2: Tập xác định của hàm số \(y = \sqrt {2 – x} + \frac{x}{{\sqrt {7 + x} }}\) là
A. \(\left[ {2; + \infty } \right)\).
B. \(\left( { – 7;2} \right]\).
C. \(\mathbb{R}\backslash \left\{ { – 7;2} \right\}\).
D. \(\left( { – 7;2} \right)\)
Phương pháp
– Phân thức xác định khi mẫu thức khác 0
– Căn thức xác định khi biểu thức trong căn lớn hơn bằng 0.
Lời giải
Chọn B
Hàm số xác định khi \(\left\{ \begin{array}{l}2 – x \ge 0\\7 + x > 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x \le 2\\x > – 7\end{array} \right.\). Vậy tập xác định của hàm số là \(\left( { – 7;2} \right]\)
Câu 3: Cho hàm số bậc hai \(y = a{x^2} + bx + c\) \(y = a{x^2} + bx + c\) có đồ thị \(y = a{x^2} + bx + c\), đỉnh của \(y = a{x^2} + bx + c\) được xác định bởi công thức nào?
A. \(y = a{x^2} + bx + c\).
B. \(y = a{x^2} + bx + c\).
C. \(y = a{x^2} + bx + c\).
D. \(y = a{x^2} + bx + c\).
Phương pháp
Tọa độ đỉnh của (P):\(y = a{x^2} + bx + c\)\(y = a{x^2} + bx + c\) là \(y = a{x^2} + bx + c\)
Lời giải
Chọn A
Tọa độ đỉnh của (P):\(y = a{x^2} + bx + c\)\(y = a{x^2} + bx + c\) là \(y = a{x^2} + bx + c\)
Câu 4: Đồ thị dưới đây là của hàm số nào?
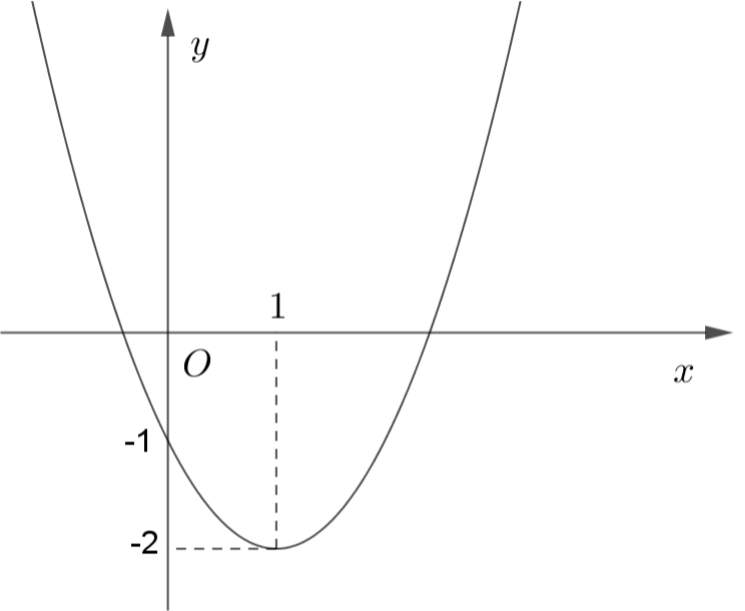
A. \(y = {x^2} + x – 4\).
B. \(y = {x^2} – 2x – 1\).
C. \(y = – {x^2} – 2x + 1\).
D. \(y = 2x – 4\).
Phương pháp
Hình dáng của đồ thị bậc hai Parabol.
Lời giải
Chọn B
Đây là đồ thị của hàm số bậc hai nên loại đáp án D
Bề lõm quay lên tức \(a > 0\)nên loại đáp án C
Đồ thị có trục đối xứng là \(x = 1\)nên ta chọn hàm số \(y = {x^2} – 2x – 1\)
Câu 5: Cho tam thức \(f(x) = a{x^2} + bx + c\,(a > 0),\,\,\Delta = {b^2} – 4ac\). Mệnh đề nào sau đây đúng?
A. \(f(x) \ge 0\,\)với mọi x thuộc \({\rm{R}}\) khi \(\Delta > 0\).
B. \(f(x) < 0\,\)với mọi x thuộc \({\rm{R}}\) khi \(\Delta < 0\).
C. \(f(x) < 0\,\)với mọi x thuộc \({\rm{R}}\) khi \(\Delta = 0\).
D. \(f(x) > 0\,\)với mọi x thuộc \({\rm{R}}\) khi \(\Delta < 0\).
Phương pháp
Sử dụng quy tắc dấu của tam thức bậc hai
Lời giải
Chọn D
\(f(x) > 0\,\)với mọi x thuộc \({\rm{R}}\) khi \(\Delta < 0\).
Câu 6: Tập nghiệm của bất phương trình \( – {x^2} + 3x \le 0\) là
A. \(\left( { – \infty \,;\,0} \right) \cup \left( {3\,;\, + \infty } \right)\).
B. \(\left( { – \infty \,;\,0} \right] \cup \left[ {3\,;\, + \infty } \right)\).
C. \(\left( {0\,;\,3} \right)\).
D. \(\left[ {0\,;\,3} \right]\).
Phương pháp
Sử dụng quy tắc dấu của tam thức bậc hai
Lời giải
Chọn B
Tam thức \(f\left( x \right) = – {x^2} + 3x\) có hai nghiệm \({x_1} = 0\,;\,{x_2} = 3\), hệ số \(a = – 1 < 0\). Do đó tập nghiệm của bất phương trình \( – {x^2} + 3x \le 0\) là \(\left( { – \infty \,;\,0} \right] \cup \left[ {3\,;\, + \infty } \right)\).
Câu 7: Giá trị \(x = 2\)là nghiệm của phương trình nào sau đây?
A. \(\sqrt {{x^2} – x – 4} = \sqrt {x – 4} \).
B. \(x – 2 = \sqrt {x – 3} \).
C. \(x + 2 = 2\sqrt {3x – 2} \).
D. \(x + 2 = \sqrt {x + 1} \).
Phương pháp
Thử giá trị của x vào phương trình trong các đáp án.
Lời giải
Chọn C
Ta thay \(x = 2\) vào pt có: \(2 + 2 = 2\sqrt {3.2 – 2} \Leftrightarrow 4 = 4\)
Câu 8: Tập nghiệm \(S\) của phương trình \(\sqrt {2x – 3} = x – 3\) là:
A. \(S = \left\{ 6 \right\}.\)
B. \(S = \emptyset .\)
C. \(S = \left\{ {6;2} \right\}.\)
D. \(S = \left\{ 2 \right\}.\)
Phương pháp
Thử các giá trị của x trong đáp án vào phương trình.
Lời giải
Chọn A
\(\sqrt {2x – 3} = x – 3 \Leftrightarrow \left\{ \begin{array}{l}x \ge 3\\2x – 3 = {x^2} – 6x + 9\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x \ge 3\\\left[ \begin{array}{l}x = 2\\x = 6\end{array} \right.\end{array} \right. \Leftrightarrow x = 6.\)
Cách 2: thử đáp án.
Thay \(x = 2\) vào phương trình ta được \(\sqrt {2.2 – 3} = 2 – 3\) (sai).
Thay \(x = 6\) vào phương trình ta được \(\sqrt {2.6 – 3} = 6 – 3\) (đúng).
Vậy \(x = 6\) là nghiệm của phương trình.
Câu 9: Trong mặt phẳng với hệ trục tọa độ \(Oxy\), cho đường thẳng \(d:2x – 3y + 1 = 0\). Vectơ nào dưới đây là vectơ pháp tuyến của đường thẳng \(d\)?
A. \(\overrightarrow {{n_2}} = (2;3)\).
B. \(\overrightarrow {{n_3}} = (3;2)\).
C. \(\overrightarrow {{n_1}} = (2; – 3)\).
D. \(\overrightarrow {{n_4}} = ( – 3;2)\).
Phương pháp
Vecto pháp tuyến của đường thẳng \(d:ax + by + c = 0\) là \(\overrightarrow n = \left( {a;b} \right)\)
Lời giải
Chọn C
Câu 10: Phuong trình tổng quát đường thẳng đi qua A(1; 3) có vectơ pháp tuyến có dạng:
A. \(2x – 3y + 3 = 0\)
B. \(3x – 2y + 1 = 0\)
C. \(3x – 2y + 3 = 0\)
D. \(2x + 3y – 1 = 0\)
Phương pháp
Phương trình tổng quát của đường thẳng đi qua điểm \(A\left( {{x_0},{y_0}} \right)\) và nhận \(\overrightarrow n = \left( {a;b} \right)\) làm vecto pháp tuyến là : \(d:a(x – {x_0}) + b(y – {y_0}) = 0\)
Lời giải
Chọn C
Phương trình đường thẳng đi qua A(1; 3)và có vtpt
\(3(x – 1) – 2(y – 3) = 0 \Leftrightarrow 3x – 2y + 3 = 0\)
Câu 11: Cho 2 điểm \(A\left( {1; – 4} \right)\),\(B\left( {1;{\rm{ }}2} \right)\). Viết phương trình tổng quát đường trung trực của đoạn thẳng \(AB\).
A. \(y – 1 = 0\).
B. \(x – 4y = 0\).
C. \(x – 1 = 0\).
D. \(y + 1 = 0\).
Phương pháp
Phương trình tổng quát của đường thẳng đi qua điểm \(A\left( {{x_0},{y_0}} \right)\) và nhận \(\overrightarrow n = \left( {a;b} \right)\) làm vecto pháp tuyến là : \(d:a(x – {x_0}) + b(y – {y_0}) = 0\)
Lời giải
Chọn D
Ta có \(\overrightarrow {AB} = \left( {0;\,6} \right) = 6\left( {0;\,1} \right)\)
Gọi là \(I\) trung điểm \(AB\). Tọa độ điểm \(I\left( {1;\, – \,1} \right)\).
Đường trung trực của đoạn thẳng \(AB\) đi qua \(I\)và nhận \(\overrightarrow {{u_{AB}}} = \left( {0;\,1} \right)\) là vectơ pháp tuyến nên phương trình đường trung trực của đoạn thẳng \(AB\) có dạng: \(0\left( {x – 1} \right) + y + 1 = 0 \Rightarrow y + 1 = 0\).
Câu 12: Khoảng cách từ \(I(1; – 2)\) đến đường thẳng \(\Delta :3x – 4y – 26 = 0\) bằng
A. \(3\). B. \(12\). C. \(5\). D. \(\frac{5}{3}\).
Phương pháp
Khoảng cách từ điểm \(M({x_0};{y_0})\) đến đường thẳng \(\Delta :{\rm{ }}ax + by + c = 0\) là: \(d(M,\Delta ) = \frac{{\left| {a{x_0} + b{y_0} + c} \right|}}{{\sqrt {{a^2} + {b^2}} }}\)
Lời giải
Chọn A
Vậy khoảng cách từ \(I(1; – 2)\) đến đường thẳng \(\Delta :3x – 4y – 26 = 0\) bằng \(d(I,\Delta ) = \frac{{\left| {3.1 – 4.( – 2) – 26} \right|}}{{\sqrt {{3^2} + {{( – 4)}^2}} }} = 3\)
Câu 13: Cho \(\Delta :x – 3y + 1 = 0\)và .\(d:3x – y – 1 = 0\) Vị trí của và d là:
A. Song song với nhau.
B. Trùng nhau
C. Vuông góc với nhau.
D. Cắt nhau nhưng không vuông góc với nhau.
Phương pháp
Sử dụng công thức vị trí tương đối của hai đường thẳng.
Lời giải
Chọn D
Ta có \(\frac{1}{3} \ne \frac{{ – 3}}{{ – 1}} \Rightarrow \)d cắt \(\Delta \). Mặt khác ta có
.\(\overrightarrow {{n_d}} .\overrightarrow {{n_\Delta }} = 1.3 + ( – 3).( – 1) = 6 \ne 0\) Vậy \(\Delta \) cắt d và không vuông góc với nhau.
Câu 14: Góc giữa hai đường thẳng \(a:\,\sqrt 3 x – y + 7 = 0\) và \(b:x – \sqrt 3 y – 1 = 0\)là:
A. \(30^\circ \). B. \(90^\circ \). C. \(60^\circ \). D. \(45^\circ \).
Phương pháp
Áp dụng công thức tính góc giữa hai đường thẳng có: \(\cos \left( {a,b} \right) = \frac{{\overrightarrow {{n_1}} .\overrightarrow {{n_2}} }}{{\left| {\overrightarrow {{n_1}} } \right|.\left| {\overrightarrow {{n_2}} } \right|}}\).
Lời giải
Chọn A
Đường thẳng \(a\) có vectơ pháp tuyến là: \(\overrightarrow {{n_1}} = \left( {\sqrt 3 ;\, – 1} \right)\);
Đường thẳng \(b\) có vectơ pháp tuyến là: \(\overrightarrow {{n_2}} = \left( {1;\, – \sqrt 3 } \right)\).
Áp dụng công thức tính góc giữa hai đường thẳng có:
\(\cos \left( {a,b} \right) = \frac{{\overrightarrow {{n_1}} .\overrightarrow {{n_2}} }}{{\left| {\overrightarrow {{n_1}} } \right|.\left| {\overrightarrow {{n_2}} } \right|}} = \frac{{1.\sqrt 3 + \left( { – 1} \right)\left( { – \sqrt 3 } \right)}}{{2.2}} = \frac{{\sqrt 3 }}{2}\). Suy ra góc giữa hai đường thẳng bằng \(30^\circ \).
Câu 15: Trong mặt phẳng tọa độ \(Oxy\), phương trình nào sau đây là phương trình của đường tròn?
A. \({x^2} + 2{y^2} – x + 8y + 1 = 0\).
B. \({x^2} + {y^2} + 4x + 6y – 12 = 0\).
C. \({x^2} + {y^2} – 2x – 8y + 25 = 0\).
D. \(4{x^2} – 4{y^2} + 9x – 6y – 1 = 0\).
Phương pháp
Phương trình đường tròn (O) có tâm I(a,b) và bán kính R là : \({(x – a)^2} + {(y – b)^2} = {R^2}\)
Lời giải
Chọn B
Để là phương trình đường tròn thì điều kiện cần là hệ số của \({x^2}\) và \({y^2}\) phải bằng nhau nên loại được đáp án A và D.
Ta có: \({x^2} + {y^2} – 2x – 8y + 25 = 0 \Leftrightarrow {\left( {x – 1} \right)^2} + {\left( {y – 4} \right)^2} + 8 = 0\) vô lý.
Ta có:\({x^2} + {y^2} + 4x + 6y – 12 = 0 \Leftrightarrow {\left( {x + 2} \right)^2} + {\left( {y + 3} \right)^2} = 25\) là phương trình đường tròn tâm \(I\left( { – 2; – 3} \right)\), bán kính \(R = 5\).
Câu 16: Xác định tâm và bán kính của đường tròn \(\left( C \right):{\left( {x + 1} \right)^2} + {\left( {y – 2} \right)^2} = 9.\)
A. Tâm \(I\left( { – 1;2} \right),\) bán kính \(R = 3\).
B. Tâm \(I\left( { – 1;2} \right),\) bán kính \(R = 9\).
C. Tâm \(I\left( {1; – 2} \right),\) bán kính \(R = 3\).
D. Tâm \(I\left( {1; – 2} \right),\) bán kính \(R = 9\).
Phương pháp
Phương trình đường tròn (O) có tâm I(a,b) và bán kính R là : \({(x – a)^2} + {(y – b)^2} = {R^2}\)
Lời giải
Chọn A
Câu 17: Cho phương trình \({x^2} + {y^2} – 2mx – 4\left( {m – 2} \right)y + 6 – m = 0\,(1)\). Điều kiện của \(m\)để \((1)\)là phương trình của đường tròn.
A. \(m = 2\).
B. \(\left[ \begin{array}{l}m 2\end{array} \right.\).
C. \(1 < m < 2\).
D. \(\left[ \begin{array}{l}m = 1\\m = 2\end{array} \right.\).
Phương pháp
Phương trình đường tròn (O) có tâm I(a,b) và bán kính R là : \({(x – a)^2} + {(y – b)^2} = {R^2}\)
Lời giải
Chọn B
\({x^2} + {y^2} – 2mx – 4\left( {m – 2} \right)y + 6 – m = 0\,(1)\)là phương trình của đường tròn khi và chỉ khi \({\left( m \right)^2} + {\left[ {2\left( {m – 2} \right)} \right]^2} – \left( {6 – m} \right) > 0 \Leftrightarrow 5{m^2} – 15m + 10 > 0 \Leftrightarrow \left[ \begin{array}{l}m 2\end{array} \right.\).
Câu 18: Trong mặt phẳng với hệ trục tọa độ \(Oxy\), cho đường tròn\((C)\) có tâm \(I(1; – 2)\) và bán kính \(R = 3\). Viết phương trình của đường tròn (C).
A. \({(x + 1)^2} + {(y – 2)^2} = 9\).
B. \({(x – 1)^2} + {(y + 2)^2} = 3\).
C. \({(x – 1)^2} – {(y + 2)^2} = 9\).
D. \({(x – 1)^2} + {(y + 2)^2} = 9\).
Phương pháp
Phương trình đường tròn (O) có tâm I(a,b) và bán kính R là : \({(x – a)^2} + {(y – b)^2} = {R^2}\)
Lời giải
Chọn D
Câu 19: Parbol \(5{y^2} = 12x\)có tiêu điểm là:
A. \(\left( {\frac{3}{5};0} \right)\).
B. \(\left( {\frac{6}{5};0} \right)\).
C. \(\left( {\frac{{12}}{5};0} \right)\).
D. \(\left( {\frac{3}{{10}};0} \right)\).
Phương pháp
Phương trình chính tắc của parabol: \({y^2} = 2px,p > 0\)
Tiêu điểm của parabol là \(F\left( {\frac{p}{2};0} \right)\)
Lời giải
Chọn A
Từ phương trình chính tắc của parabol: \({y^2} = 2px,p > 0\) ta có \(p = \frac{{12}}{5}\).
Tiêu điểm của parabol là \(F\left( {\frac{p}{2};0} \right) \Rightarrow F\left( {\frac{3}{5};0} \right)\)
Câu 20: Phương trình chính tắc của e líp có độ dài trục lớn bằng , trục nhỏ bằng là:
A. \(\frac{{{x^2}}}{{64}} + \frac{{{y^2}}}{{36}} = 1\).
B. \(\frac{{{x^2}}}{{16}} – \frac{{{y^2}}}{9} = 1\).
C. \(\frac{{{x^2}}}{9} + \frac{{{y^2}}}{{16}} = 1\).
D. \(\frac{{{x^2}}}{{16}} + \frac{{{y^2}}}{9} = 1\).
Phương pháp
Phương trình Elip \(\left( E \right):\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1\)
Lời giải
Chọn D
Theo bài ra ta có độ dài trục lớn\(2a = 8 \Rightarrow a = 4\)
Độ dài trục nhỏ \(2b = 6 \Rightarrow a = 3\)
Vậy phương trình chính tắc của e líp là \(\frac{{{x^2}}}{{16}} + \frac{{{y^2}}}{9} = 1\)
Câu 21: Bình có 4 cây bút chì khác nhau và 5 cây bút mực khác nhau. Bình cần chọn một cây bút để tặng bạn, hỏi Bình có bao nhiêu cách chọn?
A. \(5.\) B. \(4.\) C. \(9.\) D. \(20.\)
Phương pháp
Áp dụng quy tắc cộng
Lời giải
Chọn C
Theo quy tắc cộng ta có: \(5 + 4 = 9\)
Câu 22: Một người vào cửa hàng ăn, người đó chọn thực đơn gồm \(1\) món ăn trong \(5\) món, \(1\) loại quả tráng miệng trong \(5\) loại quả tráng miệng và một nước uống trong \(3\) loại nước uống. Có bao nhiêu cách chọn thực đơn.
A. \(25\). B. \(75\). C. \(100\). D. \(15\).
Phương pháp
Áp dụng quy tắc nhân
Lời giải
Chọn B
Theo quy tắc nhân ta có: \(5.5.3 = 75\) cách chọn thực đơn.
Câu 23: Từ các số \(1,2,3\) có thể lập được bao nhiêu số tự nhiên khác nhau và mỗi số có các chữ số khác nhau:
A. \(36\) B. \(20\). C. \(72\). D. \(15\).
Phương pháp
Áp dụng quy tắc đếm
Lời giải
Chọn D
TH1: số có \(1\) chữ số thì có \(3\) cách.
TH2: số có \(2\) chữ số và mỗi số có các chữ số khác nhau thì có\(3.2 = 6\)số.
TH3: số có \(3\) chữ số và mỗi số có các chữ số khác nhau thì có\(3.2.1 = 6\)số
Vậy có\(3 + 6 + 6 = 15\)số.
Câu 24: Cho hai số tự nhiên \(k,\,\,n\) thỏa \(1 \le k \le n\). Mệnh đề nào sau đây đúng?
A. \(A_n^k = \frac{{n!}}{{k!(n – k)!}}.\)
B. \(A_n^k = \frac{{k!(n – k)!}}{{n!}}.\)
C. \(A_n^k = \frac{{n!}}{{\left( {n – k} \right)!}}.\)
D. \(A_n^k = \frac{{(n – k)!}}{{n!}}.\)
Phương pháp
Áp dụng công thức chỉnh hợp : \(A_n^k = \frac{{n!}}{{\left( {n – k} \right)!}}.\)
Lời giải
Chọn C
Ta có \(A_n^k = \frac{{n!}}{{\left( {n – k} \right)!}}.\)
Câu 25: Có bao nhiêu cách xếp 6 bạn thành một hàng dọc?
A. \({6^6}\). B. \(5!\). C. \(6\). D. \(6!\).
Phương pháp
Áp dụng công thức hoán vị
Lời giải
Chọn D
Mỗi cách xếp là một hoán vị. Số cách xếp là\(6!\)
Câu 26: Tổ 1 của lớp 10A có 10 học sinh gồm 6 nam và 4 nữ. Cô giáo chủ nhiệm chọn 7 em đi lao động, trong đó có 4 nam và 3 nữ. Hỏi cô giáo chủ nhiệm có tất cả bao nhiêu cách chọn?
A. \(19.\) B. \(120.\) C. \(8640.\) D. \(60.\)
Phương pháp
Áp dụng công thức tổ hợp
Lời giải
Chọn D
Số cách chọn: \(C_6^4.C_4^3 = 60\)
Câu 27: Có 5 quyển sách khác nhau gồm 3 quyển sách Văn và 2 quyển sách Toán. Hỏi có bao nhiêu cách xếp 5 quyển sách trên lên kệ sách dài (xếp hàng ngang) sao cho tất cả quyển sách cùng môn phải đứng cạnh nhau?
A. 12 cách. B. 24 cách. C. 120 cách. D. 16 cách.
Phương pháp
Áp dụng công thức hoán vị
Lời giải
Chọn B
Các quyển sách cùng môn ta xếp chung một nhóm
Có 2 cách xếp hai nhóm môn Toán và văn
Có \(3!\)cách xếp sách Văn
Có\(2!\) cách xếp sách Toán
Vậy có\(3!.2!.2 = 24\) cách xếp sao cho tất cả quyển sách cùng môn phải đứng cạnh nhau
Câu 28: Cho hai đường thẳng song song \(a\) và \(b\). Trên đường thẳng \(a\) có 5 điểm phân biệt, trên đường thẳng \(b\) có 7 điểm phân biệt. Tính số tam giác có 3 đỉnh lấy từ các điểm trên hai đường thẳng \(a\) và \(b\).
A. 175 tam giác. B. 220 tam giác. C. 45 tam giác. D. 350 tam giác.
Phương pháp
Áp dụng công thức tổ hợp
Lời giải
Chọn B
TH1: Chọn một trên đường thẳng \(a\)và hai điểm trên đường thẳng \(b\)có\(5.C_7^2 = 105\):Tam giác
TH1: Chọn hai trên đường thẳng \(a\)và một điểm trên đường thẳng \(b\)có\(7.C_5^2 = 70\):Tam giác
Vậy có\(105 + 70 = 175\) tam giác
Câu 29: Khai triển nhị thức \({\left( {2x + y} \right)^5}\). Ta được kết quả là
A. \(32{x^5} + 16{x^4}y + 8{x^3}{y^2} + 4{x^2}{y^3} + 2x{y^4} + {y^5}\).
B. \(32{x^5} + 80{x^4}y + 80{x^3}{y^2} + 40{x^2}{y^3} + 10x{y^4} + {y^5}\).
C. \(2{x^5} + 10{x^4}y + 20{x^3}{y^2} + 20{x^2}{y^3} + 10x{y^4} + {y^5}\).
D. \(32{x^5} + 10000{x^4}y + 80000{x^3}{y^2} + 400{x^2}{y^3} + 10x{y^4} + {y^5}\).
Phương pháp
Sử dụng công thức khai triển nhị thức Newton
Lời giải
Chọn B
\({\left( {2x + y} \right)^5} = C_5^0{\left( {2x} \right)^5} + C_5^1{\left( {2x} \right)^4}y + C_5^2{\left( {2x} \right)^3}{y^2} + C_5^3{\left( {2x} \right)^2}{y^3} + C_5^4\left( {2x} \right){y^4} + C_5^5{y^5}\)\( = 32{x^5} + 80{x^4}y + 80{x^3}{y^2} + 40{x^2}{y^3} + 10x{y^4} + {y^5}\)
Câu 30: Gieo 3 đồng tiền là một phép thử ngẫu nhiên có không gian mẫu là:
A. {NN, NS, SN, SS}
B. .{NNN, SSS, NNS, SSN, NSN, SNS}
C. .{NNN, SSS, NNS, SSN, NSN, SNS, NSS,SNN}
D. .{NNN, SSS, NNS, SSN, NSS, SNN}
Phương pháp
Quy tắc đếm trong xác suất
Lời giải
Chọn C
Ta có
Câu 31: Cho A là một biến cố liên quan phép thử T. Mệnh đề nào sau đây là mệnh đề đúng?
A. là số lớn hơn 0.
B. \(0 \le P(A) \le 1\).
C. .\(P(A) = 0 \Leftrightarrow A = \Omega \)
D. là số nhỏ hơn 1.
Phương pháp
Công thức tính xác suất
Lời giải
Chọn B
\(0 \le P(A) \le 1\)
Câu 32: Gieo một đồng tiền liên tiếp lần. Số phần tử của không gian mẫu \(n(\Omega )\)là?
A. 1. B. 2. C. 4. D. 8.
Phương pháp
Quy tắc đếm trong xác suất
Lời giải
Chọn C
\(n(\Omega ) = 4\)
Câu 33: Gieo một con súc sắc. Xác suất để mặt chấm chẵn xuất hiện là:
A. 0,2. B. 0,3. C. 0,4. D. 0,5.
Phương pháp
Công thức tính xác suất
Lời giải
Chọn D
Không gian mẫu:
Biến cố xuất hiện mặt chẵn:
Suy ra .
Câu 34: Một hộp đựng bi xanh và bi đỏ, lần lượt rút viên bi. Xác suất để rút được một bi xanh và 1 bi đỏ là:
A. \(\frac{2}{{15}}\)
B.\(\frac{6}{{25}}\)
C. \(\frac{8}{{25}}\).
D. \(\frac{4}{{15}}\).
Phương pháp
Công thức tính xác suất
Lời giải
Chọn D
Phép thử: Rút lần lượt hai viên bi
Ta có: Biến cố : Rút được một bi xanh, một bi đỏ
Câu 35: Có hai hộp bi, hộp thứ nhất có 4 bi đỏ và 3 bi trắng, hộp thứ hai có 2 bi đỏ và 4 bi trắng. Chọn ngẫu nhiên mỗi hộp ra 1 viên bi. Tính xác suất \(P\) để chọn được hai viên bi cùng màu.
A. \(P = \frac{8}{{21}}\).
B. \(P = \frac{3}{7}\).
C. \(P = \frac{{10}}{{21}}\).
D. \(P = \frac{4}{9}\).
Phương pháp
Công thức tính xác suất
Lời giải
Chọn C
Phép thử: Rút mỗi hộp một viên bi
Ta có \(n(\Omega ) = 7.6 = 42\)
Biến cố : Rút được hai viên bi cùng mẫu
TH1: Hai viên màu đỏ có \(4.2 = 8\)cách
TH2: Hai viên màu trắng có\(3.4 = 12\) cách
\(n(A) = 12 + 8 = 20 \Rightarrow P(A) = \frac{{n(A)}}{{n(\Omega )}} = \frac{{20}}{{42}} = \frac{{10}}{{21}}\).
II. TỰ LUẬN (04 câu – 3,0 điểm)
Câu 36: Tìm \(m\) để bất phương trình \({x^2} – 2\left( {m + 1} \right)x + 2{m^2} – 5m + 11 < 0\) vô nghiệm.
Phương pháp
Dấu của tam thức bậc hai
Lời giải
Bất phương trình vô nghiệm khi \({x^2} – 2\left( {m + 1} \right)x + 2{m^2} – 5m + 11 \ge 0\,\,\forall \,x \in \mathbb{R}\)
\( \Leftrightarrow \left\{ \begin{array}{l}a = 1 > 0\\\Delta ‘ \le 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}1 > 0\\{m^2} + 2m + 1 – \left( {2{m^2} – 5m + 11} \right) \le 0\end{array} \right.\) \( \Leftrightarrow – {m^2} + 7m – 10 \le 0 \Leftrightarrow \left[ \begin{array}{l}m \le 2\\m \ge 5\end{array} \right.\)
Vậy \(m \in \left( { – \infty \,;\,2} \right] \cup \left[ {5\,;\, + \infty } \right)\).
Câu 37: Khi du lịch đến thành phố St. Louis (Mỹ), ta sẽ thấy một cái cổng lớn có hình parabol hướng bề lõm xuống dưới, đó là cổng Arch. Giả sử ta lập một hệ toạ độ Oxy sao cho một chân cổng đi qua gốc O như Hình 16 (x và y tính bằng mét), chân kia của cổng ở vị trí có tọa độ ( 163,0) . Biết một điểm M trên cổng có toạ độ là (10,43).
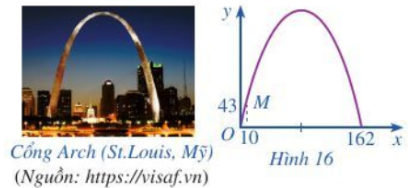
Tính chiều cao của cổng (tính từ điểm cao nhất trên cổng xuống mặt đất), làm tròn kết quả đến hàng đơn vị.
Phương pháp
Hình dáng của đồ thị bậc hai
Lời giải
Từ đồ thị ta thấy các điểm thuộc đồ thị là:\(O(0;0),M(10;43),A(162;0)\)
Gọi hàm số là
Thay tọa độ các điểm \(O,M,A\) vào ta được hệ:
\(\left\{ \begin{array}{l}a{.0^2} + b.0 + c = 0\\a{.10^2} + b.10 + c = 43\\a{.162^2} + b.162 + c = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}c = 0\\100.a + 10b = 43\\a{.162^2} + b.162 = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}c = 0\\a = – \frac{{43}}{{1520}}\\b = \frac{{3483}}{{760}}\end{array} \right.\)
Từ đó ta có \(y = – \frac{{43}}{{1520}}{x^2} + \frac{{3483}}{{760}}x\)
Hoành độ đỉnh của đồ thị là: \(x = – \frac{b}{{2a}} = 81\)
Khi đó: \(y = – \frac{{43}}{{1520}}{81^2} + \frac{{3483}}{{760}}.81 \approx 186\)(m)
Vậy chiều cao của cổng là 186m.
Câu 38: Trong mặt phẳng với hệ trục tọa độ Oxy, cho hai điểm \(A(2;0)\), \(B( – 2;2)\) và đường thẳng \(d:3x + 4y + 11 = 0\).
a. Viết phương trình chính tắc của Elip (E), biết (E) có độ dài trục lớn bằng 6 và có một tiêu điểm là A.
b. Gọi (C) là đường tròn đường kính AB; tìm điểm M trên đường thẳng d sao cho qua M vẽ được
hai tiếp tuyến MP, MQ đến (C) (P,Q là hai tiếp điểm) mà đoạn thẳng PQ có độ dài nhỏ nhất.
Phương pháp
Phương trình Elip \(\left( E \right):\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1\)
Lời giải
a. phương trình chính tắc của elip (E) có dạng \(\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1\,\,(a > b > 0).\)
+ (E) có độ dài trục lớn bằng 6 nên a=3.
+ (E) có một tiêu điểm là \(A(2;0)\) nên c=2.
\(c = 2 \Leftrightarrow {c^2} = 4 \Leftrightarrow {a^2} – {b^2} = 4 \Leftrightarrow {3^2} – {b^2} = 4 \Leftrightarrow {b^2} = 5\).
Suy ra phương trình chính tắc của elip (E) là \(\frac{{{x^2}}}{9} + \frac{{{y^2}}}{5} = 1\,\,\)
b.

+ Đường tròn (C) có tâm I(0;1), bán kính
\(R = \sqrt 5 \).
+ \(d\left( {I,d} \right) = 3 > R\) nên (C) và d không có điểm chung.
+ Gọi H là trung điểm của PQ. Suy ra PQ có độ dài nhỏ nhất khi PH có độ dài nhỏ nhất.
+ \(\frac{1}{{P{H^2}}} = \frac{1}{5} + \frac{1}{{P{M^2}}}\). Suy ra PH có độ dài nhỏ nhất khi PM có độ dài nhỏ nhất.
+ \(P{M^2} = I{M^2} – 5\). Suy ra PM có độ dài nhỏ nhất khi IM có độ dài nhỏ nhất.
+ IM có độ dài nhỏ nhất khi M là hình chiếu vuông góc của I lên d.
+ Xác định được điểm \(M\left( { – \frac{9}{5}; – \frac{7}{5}} \right)\).
———- HẾT ———-