Đáp án Đề bài Đề thi học kì 1 Toán 10 – Đề số 4 – Đề thi đề kiểm tra Toán lớp 10 Kết nối tri thức.
Câu hỏi/Đề bài:
Phần 1: Trắc nghiệm (30 câu – 6 điểm)
Câu 1: Trong các câu sau, có bao nhiêu câu là mệnh đề?
a) Hãy đi nhanh lên! b) Hà Nội là thủ đô của Việt Nam.
c) \(5 + 7 + 4 = 15\) d) Năm 2018 là năm nhuận.
A. 1 B. 2 C. 3 D. 4
Câu 2: Cho số gần đúng a = 23748023 với độ chính xác d = 123. Hãy viết số quy tròn của số a.
A. 23749000. B. 23748000. C. 23746000. D. 23737000.
Câu 3: Cho tam giác ABC và điểm \(M\) thỏa mãn điều kiện \(\overrightarrow {MA} {\rm{ \;}} – \overrightarrow {MB} {\rm{ \;}} + \overrightarrow {MC} {\rm{ \;}} = \vec 0\). Mệnh đề nào sau đây sai?
A. MABC là hình bình hành. B. \(\overrightarrow {AM} {\rm{ \;}} + \overrightarrow {AB} {\rm{ \;}} = \overrightarrow {AC} \)
C. \(\overrightarrow {BA} {\rm{ \;}} + \overrightarrow {BC} {\rm{ \;}} = \overrightarrow {BM} \) D. \(\overrightarrow {MA} {\rm{ \;}} = \overrightarrow {BC} \)
Câu 4: Cho tam giác ABC có \(AB = \sqrt 5 ,{\mkern 1mu} {\mkern 1mu} AC = \sqrt 2 \) và \(\angle C = {45^0}\). Tính độ dài cạnh BC.
A. \(3\) B. \(2\) C. \(\sqrt 3 \) D. \(\sqrt 2 \)
Câu 5: Cặp số (x;y) nào là sau đây là một nghiệm của bất phương trình \(x–2y + 5 > 0\).
A. (x;y) = (0;4). B. (x;y) = (2;5). C. (x;y) = (2;3). D. (x;y) = (1;4).
Câu 6: Cho tam giác ABC và điểm \(M\) thỏa mãn điều kiện \(\overrightarrow {MA} {\rm{ \;}} – \overrightarrow {MB} {\rm{ \;}} + \overrightarrow {MC} {\rm{ \;}} = \vec 0\). Mệnh đề nào sau đây sai?
A. MABC là hình bình hành. B. \(\overrightarrow {AM} {\rm{ \;}} + \overrightarrow {AB} {\rm{ \;}} = \overrightarrow {AC} \)
C. \(\overrightarrow {BA} {\rm{ \;}} + \overrightarrow {BC} {\rm{ \;}} = \overrightarrow {BM} \) D. \(\overrightarrow {MA} {\rm{ \;}} = \overrightarrow {BC} \)
Câu 7: Tam giác ABC có \(\angle A = {45^0},{\mkern 1mu} {\mkern 1mu} c = 6,{\mkern 1mu} {\mkern 1mu} \angle B = {75^0}\). Độ dài bán kính đường tròn ngoại tiếp tam giác bằng:
A. \(8\sqrt 3 \) B. \(2\sqrt 3 \) C. \(6\sqrt 3 \) D. \(4\sqrt 3 \)
Câu 8: Cho tam giác ABC với ba cạnh a, b, c. Khi đó \(\frac{{\cos A}}{a} + \frac{{\cos B}}{b} + \frac{{\cos C}}{c}\) bằng
A. \(\frac{{{a^2} + {b^2} + {c^2}}}{{2abc}}\) B. \(\frac{{{a^2} + {b^2} + {c^2}}}{{abc}}\) C. \(\frac{{2\left( {{a^2} + {b^2} + {c^2}} \right)}}{{abc}}\) D. \(\frac{{{a^2} + {b^2} + {c^2}}}{{4abc}}\)
Câu 9: Cho hai tập hợp: \(A = \left\{ {x \in \mathbb{R}|{x^2} – 7x + 6 = 0} \right\}\)và \(B = \left\{ {x \in \mathbb{R}|\left| x \right| > 4} \right\}\). Khẳng định nào sau đây đúng?
A. \(A \cup B = A\) B. \(A \cap B = A \cup B\) C. \(\left( {A\backslash B} \right) \subset A\) D. \(B\backslash A = \emptyset \)
Câu 10: Cho các tập hợp A, B, C được minh họa bằng biểu đồ Ven như hình vẽ. Phần tô màu xám trong hình là biểu diễn của tập hợp nào sau đây?
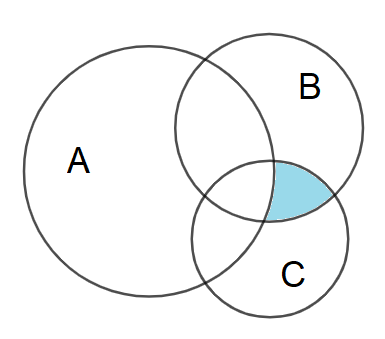
A. \(A \cap B \cap C.\) B. \(\left( {A\backslash C} \right) \cup \left( {A\backslash B} \right).\) C. \(\left( {B \cup C} \right)\backslash A.\) D. \(\left( {B \cap C} \right)\backslash A.\)
Câu 11: Để xác định chiều cao của một toà nhà cao tầng, một người đứng tại điểm M, sử dụng giác kế nhìn thấy đỉnh toà nhà với góc nâng \(\angle RQA = {79^0}\), người đó lùi ra xa một khoảng cách LM = 50 m thì nhìn thấy đỉnh toà nhà với góc nâng \(\angle RPA = {65^0}\). Hãy tính chiều cao của toà nhà (làm tròn đến chữ số thập phân thứ nhất), biết rằng khoảng cách từ mặt đất đến ống ngắm của giác kế đó là PL = QM = 1,4m.
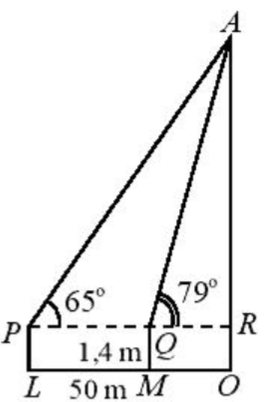
A. 135,8m B. 183,5m C. 158,3m D. 185,3m
Câu 12: Biết \(\sin x = \frac{1}{{\sqrt 3 }}\). Giá trị của biểu thức \(P = 2{\sin ^2}x – {\cos ^2}x\) là
A. \( – \frac{4}{3}\) B. \(0\) C. \(\frac{4}{3}\) D. \(\frac{2}{3}\)
Câu 13: Cho hai tập hợp: \(A = \left\{ {x \in \mathbb{R}|\left( {2{x^2} – 7x + 5} \right)\left( {x – 2} \right) = 0} \right\}\) và \(B = \left\{ {x \in \mathbb{Z}| – 3 < 2x + 1 < 5} \right\}\)
Kết luận nào sau đây là đúng?
A. \(A \cap B = \left\{ { – 1;{\mkern 1mu} {\mkern 1mu} \frac{5}{2};{\mkern 1mu} {\mkern 1mu} 2} \right\}\) B. \(A \cap B = \left\{ 1 \right\}\) C. \(A \cap B = \left\{ { – 1;{\mkern 1mu} {\mkern 1mu} 0;{\mkern 1mu} {\mkern 1mu} 2;{\mkern 1mu} {\mkern 1mu} \frac{5}{2};{\mkern 1mu} {\mkern 1mu} 2} \right\}\) D. \(A \cap B = \left\{ { – 1;{\mkern 1mu} {\mkern 1mu} 0;{\mkern 1mu} {\mkern 1mu} 1} \right\}\)
Câu 14: Cho \(\cos \alpha {\rm{ \;}} = \frac{1}{4}\). Giá trị của \(P = \frac{{\tan \alpha {\rm{ \;}} + 2\cot \alpha }}{{2\tan \alpha {\rm{ \;}} + 3\cot \alpha }}\) là:
A. \( – \frac{{17}}{{33}}\) B. \(\frac{{17}}{{33}}\) C. \(\frac{1}{2}\) D. \(\frac{{16}}{{33}}\)
Câu 15: Cho ba lực \(\overrightarrow {{F_1}} {\rm{ \;}} = \overrightarrow {MA} \), \(\overrightarrow {{F_2}} {\rm{ \;}} = \overrightarrow {MB} \), \(\overrightarrow {{F_3}} {\rm{ \;}} = \overrightarrow {MC} \) cùng tác động vào một vật tại điểm \(M\) và vật đứng yên. Cho biết cường độ của \(\overrightarrow {{F_1}} \), \(\overrightarrow {{F_2}} \) đều bằng 50N và góc \(\widehat {AMB} = {60^\circ }\). Khi đó cường độ lực \(\overrightarrow {{F_1}} \) của là
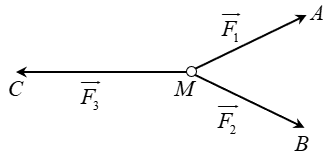
A. \(100\sqrt 3 N\) B. \(25\sqrt 3 N\) C. \(50\sqrt 3 N\) D. \(50\sqrt 2 N\)
Câu 16: Cho ba véctơ bất kì \(\vec u,\vec v,\vec w\) bất kì. Mệnh đề nào sau đây đúng?
A. \(\left| {\vec u + \vec v + \vec w} \right| \ge \left| {\vec u} \right| + \left| {\vec v} \right| + \left| {\vec w} \right|\) B. \(\left| {\vec u + \vec v} \right| \le \left| {\vec u} \right| + \left| {\vec v} \right|\)
C. \(\left| {\vec u + \vec v + \vec w} \right| \ge \left| {\vec u} \right| – \left| {\vec v} \right| + \left| {\vec w} \right|\) D. \(\left| {\vec u + \vec v} \right| \le \left| {\vec u} \right| – \left| {\vec v} \right|\)
Câu 17: Người ta chọn một số bút bi của hai hãng sản xuất A và B thử xem sử dụng một bút thì sau bao nhiêu giờ thì hết mực. Kết quả như sau (đơn vị giờ):
Loại bút A: \(\begin{array}{*{20}{c}}{23}&{25}&{27}&{28}&{30}&{35}\end{array}\)
Loại bút B: \(\begin{array}{*{20}{c}}{16}&{22}&{28}&{33}&{46}\end{array}\)
Nhận xét nào sau đây là đúng?
A. Loại bút A có thời gian sử dụng lâu hơn và chất lượng của loại bút A không đồng đều.
B. Loại bút A có thời gian sử dụng lâu hơn và chất lượng của loại bút A đồng đều.
C. Loại bút B có thời gian sử dụng lâu hơn và chất lượng của loại bút B không đồng đều.
D. Loại bút B có thời gian sử dụng lâu hơn và chất lượng của loại bút B đồng đều.
Câu 18: Phương sai của một mẫu số liệu \(\left\{ {{x_1};{x_2};…;{x_N}} \right\}\) bằng
A. Hai lần độ lệch chuẩn. B. Căn bậc hai của độ lệch chuẩn.
C. \(\sum\limits_{i = 1}^N {{{\left( {{x_i} – \bar x} \right)}^2}} .\) D. Bình phương của độ lệch chuẩn.
Câu 19: Cho tam giác ABC vuông cân tại A có AB = 6. Giá trị của \(\overrightarrow {BA} .\overrightarrow {BC} \) bằng
A. 0. B. 36. C. -36. D. \(36\sqrt 2 .\)
Câu 20: Quan sát 9 con chuột chạy quanh một căn phòng và ghi lại thời gian (tính bằng phút) của chúng trong bảng sau:

Số trung vị và Mốt của mẫu số liệu thống kê trên lần lượt là
A. 5 và 9 B. 2 và 30 C. 1,5 và 1 D. 1,5 và 2
Câu 21: (ID: 590911) Đường thẳng \(2x – 3y + 6 = 0\) chia mặt phẳng tọa độ thành các miền như hình vẽ. Miền nghiệm của \(2x – 3y + 6 \ge 0\) là:
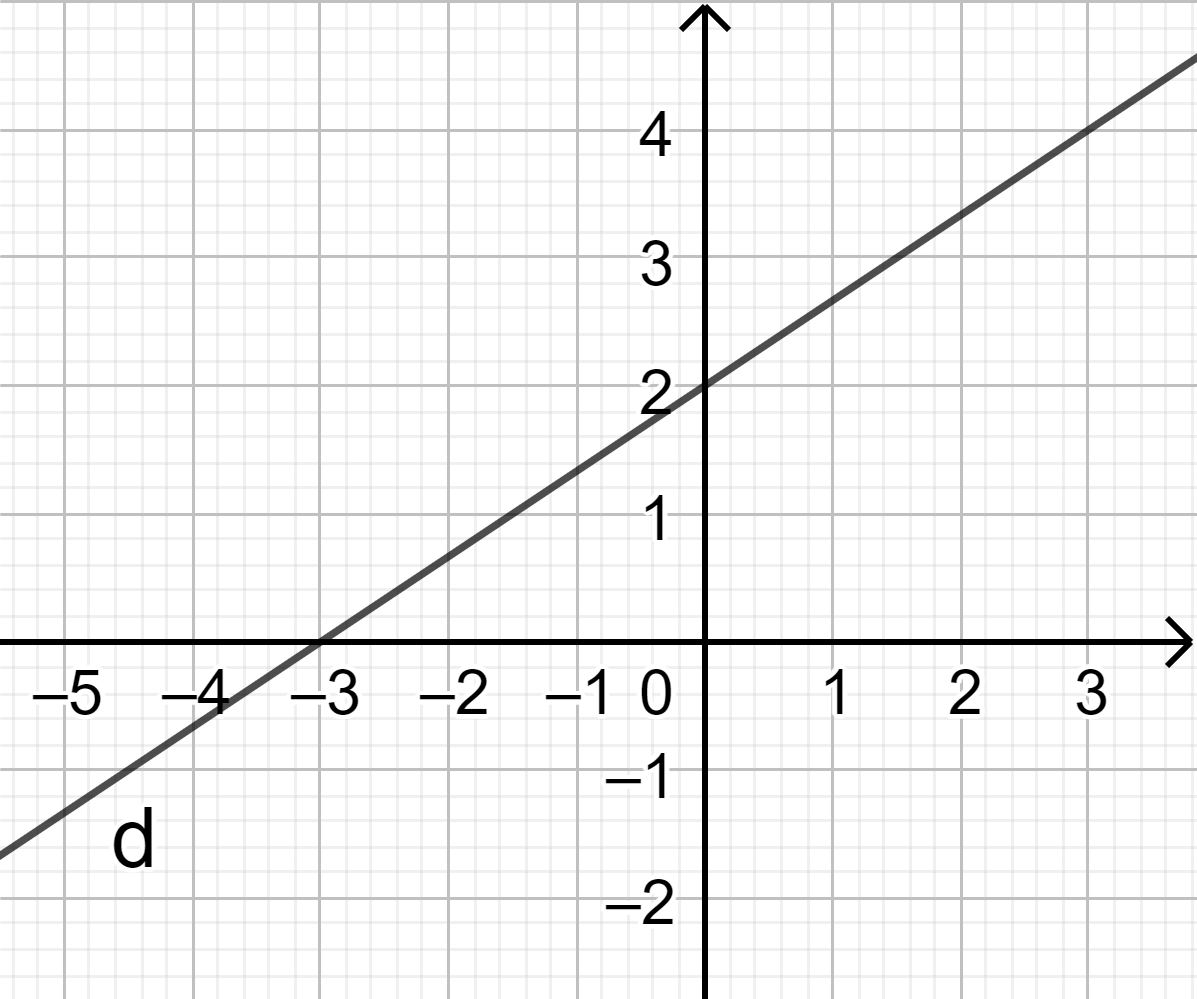
A. Nửa mặt phẳng bờ d chứa gốc tọa độ O và có lấy đường thẳng d.
B. Nửa mặt phẳng bờ d chứa gốc tọa độ O và có lấy đường thẳng d.
C. Nửa mặt phẳng bờ d không chứa gốc tọa độ O và không lấy đường thẳng d.
D. Nửa mặt phẳng bờ d không chứa gốc tọa độ O và không lấy đường thẳng d.
Câu 22: Điểm nào dưới đây thuộc miền nghiệm của hệ bất phương trình \(\left\{ {\begin{array}{*{20}{l}}{x + 2y > – 3}\\{3x – y 0}\end{array}} \right.\).
A. \(\left( { – 2; – 1} \right)\) B. \(\left( {2;0} \right)\) C. \(\left( {3;2} \right)\) D. \(\left( {0,2} \right)\)
Câu 23: Giá trị của biểu thức \(B = \cos {0^0} + \cos {20^0} + \cos {40^0} + … + \cos {160^0} + \cos {180^0}\) là
A. \(0\) B. \(1\) C. \( – 1\) D. \(\frac{1}{2}\)
Câu 24: Cho tam giác đều ABC có độ dài các cạnh bằng 6 và điểm M thỏa mãn \(\overrightarrow {BM} {\rm{ \;}} = {\rm{ \;}} – \frac{1}{3}\overrightarrow {BC} \). Tích vô hướng \(\overrightarrow {BM} .\overrightarrow {BA} \) bằng
A. \(6\) B. \( – 6\sqrt 3 .\) C. \(6\sqrt 3 .\) D. \( – 6.\)
Câu 25: Độ dài của cầu Bến Thủy 2 (Nghệ An) người ta đo được là \(996m \pm 0,5m\), có nghĩa là:
A. Độ dài đúng của cầu là một số nằm trong khoảng 995,5m đến 996,5m.
B. Độ dài đúng của cầu là một số lớn hơn 996m.
C. Độ dài đúng của cầu là một số nhỏ hơn 996m.
D. Độ dài đúng của cầu là 995,5m hoặc là 996,5m.
Câu 26: Hình chữ nhật có các cạnh \(x = 2m \pm 1cm,\,\,y = 5m \pm 2cm\). Diện tích hình chữ nhật và sai số tương đối của giá trị đó là:
A. 10m2 và 5 % B. 10m2 và 4 % C. 10m2 và 9 % D. 10m2 và 20%
Câu 27: Khoảng biến thiên của mẫu số liệu 13; 16; 9; 10; 5; 8; 11; 17; 6; 20 là:
A. 5. B. 8. C. 15. D. 20.
Câu 28: Trong đợt hội diễn văn nghệ chào mừng 20/11, lớp 10A đăng kí hai tiết mục là múa và diễn kịch. Trong danh sách, có 9 học sinh tham gia tiết mục múa, 13 học sinh tham gia diễn kịch; trong đó có 4 học sinh tham gia cả tiết mục múa và diễn kịch. Hỏi lớp 10A có tất cả bao nhiêu học sinh tham gia hội diễn văn nghệ?
A. 15. B. 18. C. 21. D. 26.
Câu 29: Cho hình vuông ABCD có cạnh bằng \(a\). Khi đó \(\left| {\overrightarrow {AB} {\rm{ \;}} + \overrightarrow {AC} } \right|\) bằng:
A. \(\frac{{a\sqrt 5 }}{2}\) B. \(\frac{{a\sqrt 3 }}{2}\) C. \(\frac{{a\sqrt 3 }}{3}\) D. \(a\sqrt 5 \)
Câu 30: Cho hai vectơ \(\vec a\) và \(\vec b\) khác \(\vec 0\). Xác định góc \(\alpha \) giữa hai vectơ \(\vec a\) và \(\vec b\) khi \(2\vec a.\vec b{\rm{ \;}} = {\rm{ \;}}\left| {\vec a} \right|.\left| {\vec b} \right|\).
A. \(\alpha {\rm{ \;}} = {180^0}.\) B. \(\alpha {\rm{ \;}} = {120^0}.\) C. \(\alpha {\rm{ \;}} = {90^0}.\) D. \(\alpha {\rm{ \;}} = {60^0}.\)
Phần 2: Tự luận (4 điểm)
Câu 1: Cho tam giác ABC.
a) Tìm điểm K sao cho \(\overrightarrow {KA} {\rm{ \;}} + 2\overrightarrow {KB} {\rm{ \;}} = \overrightarrow {CB} \).
b) Tìm điểm M sao cho \(\overrightarrow {MA} {\rm{ \;}} + 2\overrightarrow {MB} {\rm{ \;}} + 2\overrightarrow {MC} {\rm{ \;}} = \vec 0\).
Câu 2: Kết quả dự báo nhiệt độ cao nhất trong 10 ngày liên tiếp ở Nghệ An cuối tháng 01 năm 2022 được cho ở bảng sau:

(Nguồn: https://nchmf.gov.vn)
a) Viết mẫu số liệu thống kê nhiệt độ nhận được từ bảng trên.
b) Tính số trung bình cộng, phương sai và độ lệch chuẩn của mẫu số liệu đó.
Câu 3: Chứng minh rằng với mọi tam giác ABC ta có
a) \(\cot A + \cot B + \cot C = \frac{{{a^2} + {b^2} + {c^2}}}{{abc}}R\)
b) \(\sin \frac{A}{2} = \sqrt {\frac{{(p – b)(p – c)}}{{bc}}} \)
—– HẾT —–