Đáp án Lời giải Đề thi học kì 1 Toán 10 – Đề số 5 – Đề thi đề kiểm tra Toán lớp 10 Chân trời sáng tạo.
Câu hỏi/Đề bài:
HƯỚNG DẪN GIẢI CHI TIẾT
Phần 1: Trắc nghiệm (30 câu – 6 điểm)
|
1.A |
2.D |
3.B |
4.D |
5.C |
6.C |
7.D |
8.B |
9.A |
10.D |
|
11.D |
12.B |
13.C |
14.D |
15.D |
16.A |
17.A |
18.A |
19.A |
20.B |
|
21.D |
22.D |
23.B |
24.B |
25.B |
26.D |
27.C |
28.B |
29.C |
30.B |
Câu 1 (NB):
Hướng dẫn:
Mệnh đề là câu khẳng định có tính đúng hoặc sai.
Cách giải:
Bạn bao nhiêu tuổi? là câu nghi vấn nên không phải là mệnh đề.
Chọn A.
Câu 2 (NB):
Hướng dẫn:
Ta thường dùng các chữ cái in hoa để kí hiệu tập hợp và chữ cái in thường để kí hiệu phần tử thuộc tập hợp.
Cách giải:
Ta có: \(\bar a = 31975421 \pm 150 \Rightarrow \bar a \in \left[ {31975271;31975571} \right]\).
Khi làm tròn số gần đúng a ta nên làm tròn đến hàng nghìn vì chữ số hàng trăm không chắc chắn đúng.
Vậy quy tròn số gần đúng a ta được số 31975000.
Chọn D.
Câu 3 (TH):
Hướng dẫn:
Sử dụng quy tắc ba điểm.
Sử dụng hai vectơ bằng nhau.
Cách giải:
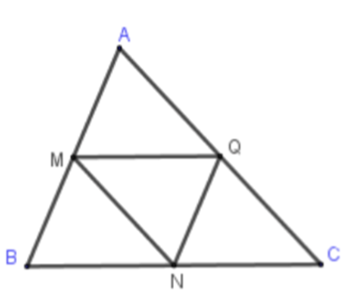
Ta có:
\(\begin{array}{*{20}{l}}{\overrightarrow {AB} {\rm{ \;}} + \overrightarrow {BM} {\rm{ \;}} + \overrightarrow {NA} {\rm{ \;}} + \overrightarrow {BQ} }\\{ = \overrightarrow {AM} {\rm{ \;}} + \overrightarrow {NA} {\rm{ \;}} + \overrightarrow {BQ} }\\{ = \overrightarrow {MB} {\rm{ \;}} + \overrightarrow {BQ} {\rm{ \;}} + \overrightarrow {NA} }\\{ = \overrightarrow {MQ} {\rm{ \;}} + \overrightarrow {NA} }\\{ = \overrightarrow {BN} {\rm{ \;}} + \overrightarrow {NA} }\\{ = \overrightarrow {BA} }\end{array}\)
Chọn B.
Câu 4 (NB):
Hướng dẫn:
Sử dụng định lí cosin trong tam giác: \(B{C^2} = A{B^2} + A{C^2} – 2AB.AC.\cos \angle BAC.\)
Cách giải:
Ta có:
\(\begin{array}{*{20}{l}}{B{C^2} = A{B^2} + A{C^2} – 2AB.AC.\cos \angle BAC.}\\{{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} = {6^2} + {8^2} – 2.6.8.\cos {{120}^0}}\\{{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} = 148}\\{ \Rightarrow BC = \sqrt {148} {\rm{ \;}} = 2\sqrt {37} .}\end{array}\)
Chọn D.
Câu 5 (NB):
Hướng dẫn:
Cặp số nào thỏa mãn bất phương trình là nghiệm của bất phương trình.
Cách giải:
Thay cặp số (x;y) = (0;4) vào bất phương trình: 0 – 4 + 3 > 0 => Sai.
Thay cặp số (x;y) = (2;5) vào bất phương trình: 2 – 5 + 3 > 0 => Sai.
Thay cặp số (x;y) = (1;3) vào bất phương trình: 1 – 3 + 3 > 0 => Đúng.
Thay cặp số (x;y) = (1;4) vào bất phương trình: 1 – 4 + 3 > 0 => Sai.
Chọn C.
Câu 6 (TH):
Hướng dẫn:
Sử dụng quy tắc hình bình hành.
Cách giải:
Theo quy tắc hình bình hành ta có:
\(\begin{array}{*{20}{l}}{\overrightarrow {AB} {\rm{ \;}} + \overrightarrow {AD} {\rm{ \;}} = \overrightarrow {AC} }\\{ \Rightarrow \overrightarrow {AB} {\rm{ \;}} + \overrightarrow {AC} {\rm{ \;}} + \overrightarrow {AD} {\rm{ \;}} = \overrightarrow {AC} {\rm{ \;}} + \overrightarrow {AC} {\rm{ \;}} = 2\overrightarrow {AC} }\\{ \Rightarrow k = 2.}\end{array}\)
Chọn C.
Câu 7 (NB):
Hướng dẫn:
Sử dụng các công thức tính diện tích tam giác: \(S = \frac{{abc}}{{4R}}\), \(S = \frac{1}{2}ab\sin C\), \(S = \frac{1}{2}\sqrt {p\left( {p – a} \right)\left( {p – b} \right)\left( {p – c} \right)} \), \(S = p.R\) với \(p = \frac{{a + b + c}}{2}.\)
Cách giải:
\(S = \frac{1}{2}ab\sin C\) nên đáp án D sai.
Chọn D.
Câu 8 (TH):
Hướng dẫn:
\(\sqrt {f(x)} \) xác định khi \(f(x) \ge 0\)
\(\frac{1}{{g(x)}}\) xác định khi \(g(x) \ne 0\)
Cách giải:
Điều kiện: \(\left\{ \begin{array}{l}{x^2} – 3x + 2 \ge 0\\x + 3 > 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x \in \left( { – \infty ;1} \right] \cup \left[ {2; + \infty } \right)\\x > – 3\end{array} \right. \Leftrightarrow x \in \left( { – 3;1} \right] \cup \left[ {2; + \infty } \right)\).
Chọn B.
Câu 9 (TH):
Hướng dẫn:
Biểu diễn các tập hợp trên trục số và thực hiện các phép toán trên tập hợp.
Cách giải:

\(P\backslash Q = \left[ { – 4; – 3} \right] \Rightarrow A\) đúng.
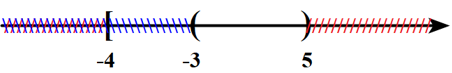
\(P \cap Q = \left( { – 3;5} \right) \Rightarrow B\) sai.
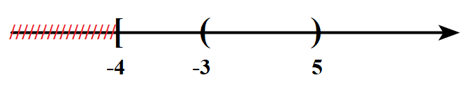
\(P \cup Q = \left[ { – 4; + \infty } \right) \Rightarrow C\) sai.
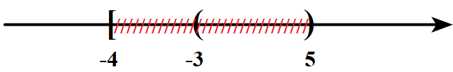
\({C_\mathbb{R}}P = \mathbb{R}\backslash P = \left( { – \infty ; – 4} \right) \cup \left[ {5; + \infty } \right) \Rightarrow D\) sai.
Chọn A.
Câu 10 (TH):
Hướng dẫn:
Sử dụng khái niệm các phép toán trên tập hợp.
Cách giải:
Phần tô đậm trong hình vẽ biểu diễn cho tập hợp \(\left( {A \cap B} \right)\backslash C.\)
Chọn D.
Câu 11 (TH):
Hướng dẫn:
Sử dụng định lí Cosin trong tam giác ABC ta có: \(A{B^2} = A{C^2} + B{C^2} – 2AC.BC.\cos C.\)
Cách giải:
Áp dụng định lí Cosin trong tam giác ABC ta có:
\(\begin{array}{*{20}{l}}{A{B^2} = A{C^2} + B{C^2} – 2AC.BC.\cos C}\\{{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} = {{200}^2} + {{180}^2} – 2.200.180.\cos {{52}^0}16′ \approx 28337}\\{ \Rightarrow AB \approx 168{\mkern 1mu} {\mkern 1mu} \left( m \right)}\end{array}\)
Chọn D.
Câu 12 (TH):
Hướng dẫn:
Dùng công thức \({\sin ^2}x + {\cos ^2}x = 1\) để tính cos x
Cách giải:
\(\begin{array}{*{20}{l}}{\sin x = \frac{1}{2} \Rightarrow \sin {x^2} = \frac{1}{4} \Rightarrow {{\cos }^2}x = 1 – {{\sin }^2}x = 1 – \frac{1}{4} = \frac{3}{4}}\\{ \Rightarrow {{\sin }^2}x – {{\cos }^2}x = \frac{1}{4} – \frac{3}{4} = \frac{{ – 1}}{2}}\end{array}\)
Chọn B.
Câu 13 (VD):
Cách giải:
TXĐ: \(D = \mathbb{R}{\rm{\backslash \{ }} – 1\} \).
Xét \({x_1};\,{x_2}\, \in \,D\)và\({x_1} < {x_2} \Leftrightarrow {x_1} – {x_2} < 0\)
Khi đó với hàm số \(y = f\left( x \right) = \frac{4}{{x + 1}}\)
\( \Rightarrow f\left( {{x_1}} \right) – f\left( {{x_2}} \right) = \frac{4}{{{x_1} + 1}} – \frac{4}{{{x_2} + 1}} = 4.\frac{{\left( {{x_2} – {x_1}} \right)}}{{\left( {{x_1} + 1} \right)\left( {{x_2} + 1} \right)}}\)
Trên \(\left( { – \infty ; – 1} \right)\)\( \Rightarrow f\left( {{x_1}} \right) – f\left( {{x_2}} \right) = 4.\frac{{\left( {{x_2} – {x_1}} \right)}}{{\left( {{x_1} + 1} \right)\left( {{x_2} + 1} \right)}} > 0\)nên hàm số nghịch biến.
Trên \(\left( { – 1; + \infty } \right)\)\( \Rightarrow f\left( {{x_1}} \right) – f\left( {{x_2}} \right) = 4.\frac{{\left( {{x_2} – {x_1}} \right)}}{{\left( {{x_1} + 1} \right)\left( {{x_2} + 1} \right)}} > 0\)nên hàm số nghịch biến.
Vậy \(y = \left| {x + 1} \right| – \left| {1 – x} \right|\)không là hàm số chẵn.
Chọn C.
Câu 14 (TH):
Hướng dẫn:
Nếu \(\alpha {\rm{ \;}} + \beta {\rm{ \;}} = {90^0}\) thì \(\sin \alpha {\rm{ \;}} = \cos \beta \).
Cách giải:
Ta có:
\(\begin{array}{*{20}{l}}{A = {{\sin }^2}{{51}^0} + {{\sin }^2}{{55}^0} + {{\sin }^2}{{39}^0} + {{\sin }^2}{{35}^0}}\\{A = \left( {{{\sin }^2}51 + {{\sin }^2}{{39}^0}} \right) + \left( {{{\sin }^2}{{55}^0} + {{\sin }^2}{{35}^0}} \right)}\\{A = \left( {{{\sin }^2}51 + {{\sin }^2}\left( {{{90}^0} – {{51}^0}} \right)} \right) + \left( {{{\sin }^2}{{55}^0} + {{\sin }^2}\left( {{{90}^0} – {{55}^0}} \right)} \right)}\\{A = \left( {{{\sin }^2}51 + {{\cos }^2}{{51}^0}} \right) + \left( {{{\sin }^2}{{55}^0} + {{\cos }^2}{{55}^0}} \right)}\\{A = 1 + 1 = 2.}\end{array}\)
Chọn D.
Câu 15 (TH):
Hướng dẫn:
Vì M đứng yên nên \(\overrightarrow {{F_1}} {\rm{ \;}} + \overrightarrow {{F_2}} {\rm{ \;}} + \overrightarrow {{F_3}} {\rm{ \;}} = \vec 0{\rm{ \;}} \Rightarrow \overrightarrow {MA} {\rm{ \;}} + \overrightarrow {MB} {\rm{ \;}} + \overrightarrow {MC} {\rm{ \;}} = \vec 0\).
Sử dụng quy tắc hình bình hành.
Cách giải:
Vì M đứng yên nên \(\overrightarrow {{F_1}} {\rm{ \;}} + \overrightarrow {{F_2}} {\rm{ \;}} + \overrightarrow {{F_3}} {\rm{ \;}} = \vec 0{\rm{ \;}} \Rightarrow \overrightarrow {MA} {\rm{ \;}} + \overrightarrow {MB} {\rm{ \;}} + \overrightarrow {MC} {\rm{ \;}} = \vec 0\).
Áp dụng quy tắc hình bình hành ta có: \(\overrightarrow {MA} {\rm{ \;}} + \overrightarrow {MB} {\rm{ \;}} = \overrightarrow {MD} \), với D là đỉnh thứ tư của hình bình hành AMBD như hình vẽ.

\(\begin{array}{*{20}{l}}{ \Rightarrow \overrightarrow {MD} {\rm{ \;}} + \overrightarrow {MC} {\rm{ \;}} = \vec 0{\rm{ \;}} \Rightarrow \overrightarrow {MC} {\rm{ \;}} = {\rm{ \;}} – \overrightarrow {MD} }\\{ \Rightarrow \left| {\overrightarrow {{F_3}} } \right| = \left| {\overrightarrow {MC} } \right| = \left| { – \overrightarrow {MD} } \right| = MD}\end{array}\)
Vì MA = MB = 100, \(\angle AMB = {60^0}\) nên tam giác AMB đều \( \Rightarrow MD = 100\sqrt 3 \).
Vậy \(\left| {\overrightarrow {{F_3}} } \right| = 100\sqrt 3 N.\)
Chọn D.
Câu 16 (TH):
Hướng dẫn:
Tọa độ đỉnh của parabol \(y = a{x^2} + bx + c\) là \(I\left( { – \frac{b}{{2a}};\frac{{ – \Delta }}{{4a}}} \right)\)
Cách giải:
Tọa độ đỉnh của parabol \(y = – 2{x^2} – 4x + 6\) là \(\left\{ \begin{array}{l}x = – \frac{{ – 4}}{{2.\left( { – 2} \right)}} = – 1\\y = – 2.{\left( { – 1} \right)^2} – 4.\left( { – 1} \right) + 6 = 8\end{array} \right. \Rightarrow I\left( { – 1;8} \right)\).
Chọn A.
Câu 17 (VD):
Hướng dẫn:
Xác định và so sánh phương sai, độ lệch chuẩn về tốc độ của 20 chiếc xe ô tô trên mỗi con đường.
Cách giải:
*) Con đường A
Bảng phân bố tần số:
![]()
Số trung bình: \(\overline {{x_A}} {\rm{\;}} = \frac{{60.2 + 65.4 + 68.2 + 72.1 + 75.2 + 76.2 + 80.2 + 84.1 + 85.2 + 90.2}}{{20}}\)\( = 74,2\left( {{\rm{km/h}}} \right)\)
Phương sai: \(s_A^2 = \frac{1}{{20}}\left[ {2.{{(60 – 74,2)}^2} + 4.{{(65 – 74,2)}^2} + … + 2.{{(90 – 74,2)}^2}} \right] = 86,36\left( {km/h} \right)\)
Độ lệch chuẩn: \({s_A} = \sqrt {s_A^2} {\rm{\;}} = \sqrt {86,36} {\rm{\;}} \approx 9,29{\mkern 1mu} {\mkern 1mu} \left( {km/h} \right)\)
*) Con đường B
Bảng phân bố tần số:
![]()
Số trung bình: \({x_B} = \frac{{55.3 + 60.1 + 62.2 + 64.2 + 70.3 + 76.2 + 79.3 + 80.2 + 85.2}}{{20}} = 70,3\left( {{\rm{km/h}}} \right)\)
Phương sai: \(s_B^2 = \frac{1}{{20}}\left[ {3.{{(55 – 70,3)}^2} + 1.{{(60 – 70,3)}^2} + … + 2.{{(85 – 70,3)}^2}} \right] = 96,91\left( {km/h} \right)\)
Độ lệch chuẩn: \({s_B} = \sqrt {s_B^2} {\rm{\;}} = \sqrt {96,91} {\rm{\;}} \approx 9,84{\mkern 1mu} {\mkern 1mu} \left( {km/h} \right)\)
Vậy xe chạy trên con đường A sẽ an toàn hơn.
Chọn A.
Câu 18 (NB):
Hướng dẫn:
Cho mẫu số liệu có kích thước \(N\) là \(\left\{ {{x_1};{\mkern 1mu} {\mkern 1mu} {x_2};{\mkern 1mu} {\mkern 1mu} \ldots ;{\mkern 1mu} {\mkern 1mu} {x_N}} \right\}\). Phương sai của mẫu số liệu này bằng trung bình của tổng các bình phương độ lệch giữa các giá trị với số trung bình.
Cách giải:
Dựa theo lý thuyết, ta có:
Dãy số liệu \({x_1},{\mkern 1mu} {\mkern 1mu} {x_2}, \ldots ,{\mkern 1mu} {\mkern 1mu} {x_N}\) có kích thước mẫu \(N\), phương sai được tính theo công thức:
\({s^2} = \frac{1}{N}\sum\limits_{i = 1}^N {{{\left( {{x_i} – \bar x} \right)}^2}} \) trong đó \(\bar x = \) trung bình cộng của mẫu số liệu
Chọn A.
Câu 19 (TH):
Hướng dẫn:
Tọa độ đỉnh của parabol \(y = a{x^2} + bx + c\) là \(I\left( { – \frac{b}{{2a}};\frac{{ – \Delta }}{{4a}}} \right)\)
Cách giải:
Đồ thị hàm số \(y = {\rm{a}}{{\rm{x}}^2} + bx + c\) đi qua điểm \(A\left( {2;1} \right)\) và có đỉnh \(I\left( {1\,;\, – 1} \right)\) nên có hệ phương trình
\(\left\{ \begin{array}{l}4a + 2b + c = 1\\ – \frac{b}{{2a}} = 1\\a + b + c = – 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}4a + 2b + c = 1\\b = – 2a\\a + b + c = – 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}c = 1\\b = – 2a\\ – a + c = – 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}c = 1\\b = – 4\\a = 2\end{array} \right.\).
Vậy \(T = {a^3} + {b^2} – 2c = 22\).
Chọn A.
Câu 20 (TH):
Hướng dẫn:
Đối với bảng phân bố tần số ghép lớp:
+ Số trung bình cộng: \(\bar x = \frac{{{c_1}{n_1} + {c_2}{n_2} + \ldots + {c_k}{n_k}}}{N}\)
+ Phương sai: \({s^2} = \frac{1}{N}\left[ {{n_1}{{\left( {{c_1} – \bar x} \right)}^2} + {n_2}{{\left( {{c_2} – \bar x} \right)}^2} + \ldots + {n_k}{{\left( {{c_k} – \bar x} \right)}^2}} \right]\)
+ Độ lệch chuẩn: \(s = \sqrt {{s^2}} \)
Với \({n_i}\) là tần số của giá trị \({c_i}\).
Cách giải:
Ta có bảng phân bố tần số, tần suất ghép lớp:
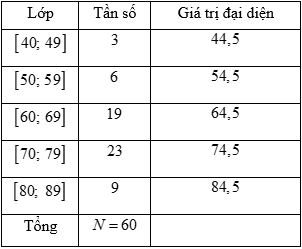
Số trung bình cộng:
\(\bar x = \frac{{44,5.3 + 54,5.6 + 64,5.19 + 74,5.23 + 84,5.9}}{{60}} = \frac{{4160}}{{60}} \approx 69,33\) (nghìn đồng)
Phương sai:
\({s^2} = \frac{1}{{60}}\left( {3.44,{5^2} + 6.54,{5^2} + 19.64,{5^2} + 23.74,{5^2} + 9.84,{5^2}} \right) – {\left( {\frac{{4160}}{{60}}} \right)^2}\)\( = \frac{{3779}}{{36}}\) (nghìn đồng)
Độ lệch chuẩn: \(s = \sqrt {{s^2}} \)\( = \sqrt {\frac{{3779}}{{36}}} {\rm{\;}} \approx 10,25\) (nghìn đồng)
Chọn B.
Câu 21 (NB):
Hướng dẫn:
Chọn điểm bất kì thỏa mãn bất phương trình để chọn miền nghiệm
Cách giải:
Vì O(0,0) không thuộc miền nghiệm nên nửa mặt phẳng có bờ là d khác phía gốc tọa độ O và không lấy đường thẳng d
Chọn D.
Câu 22 (NB):
Hướng dẫn:
Vẽ đồ thị hoặc thử các đáp án
Cách giải:
\(\left( {0,2} \right)\) thỏa mãn 3 phương trình trong hệ phương trình nên chọn D
Chọn D.
Câu 23 (TH):
Hướng dẫn:
Sử dụng định lí Sin trong tam giác \(\frac{a}{{\sin A}} = \frac{b}{{\sin B}} = \frac{c}{{\sin C}} = 2R\).
Cách giải:
Sử dụng định lí Sin trong tam giác \(\frac{a}{{\sin A}} = \frac{b}{{\sin B}} = \frac{c}{{\sin C}} = 2R\) \( \Rightarrow \left\{ {\begin{array}{*{20}{l}}{a = 2R\sin A}\\{b = 2R\sin B}\\{c = 2R\sin C}\end{array}} \right.\).
Theo giả thiết ta có:
\(\begin{array}{*{20}{l}}{{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} b + c = 2a}\\{ \Leftrightarrow 2R\sin B + 2R\sin C = 2.2R\sin A}\\{ \Leftrightarrow \sin B + \sin C = 2\sin A.}\end{array}\)
Chọn B.
Câu 24 (TH):
Hướng dẫn:
Sử dụng công thức \(\overrightarrow {BM} .\overrightarrow {BA} {\rm{ \;}} = BM.BA.\cos \left( {\overrightarrow {BM} ,\overrightarrow {BA} } \right).\)
Cách giải:
Ta có: \(\overrightarrow {BM} .\overrightarrow {BA} {\rm{ \;}} = {\rm{ \;}} – \frac{1}{2}\overrightarrow {BC} .\overrightarrow {BA} {\rm{ \;}} = {\rm{ \;}} – \frac{1}{2}BC.BA.\cos \left( {\overrightarrow {BC} ,\overrightarrow {BA} } \right).\)
Vì tam giác ABC đều nên \(\cos \left( {\overrightarrow {BC} ,\overrightarrow {BA} } \right) = \angle ABC = {60^0}\).
\( \Rightarrow \overrightarrow {BM} .\overrightarrow {BA} = – \frac{1}{2}.4.4.\frac{{\sqrt 3 }}{2} = {\rm{ \;}} – 4\sqrt 3 .\)
Chọn B.
Câu 25 (TH):
Hướng dẫn:
Tọa độ đỉnh của parabol \(y = a{x^2} + bx + c\) là \(I\left( { – \frac{b}{{2a}};\frac{{ – \Delta }}{{4a}}} \right)\)
Cách giải:
Từ BBT ta có \(a > 0\) nên loại đáp án D. Đỉnh \(I\left( {1; – 3} \right)\) nên \( – \frac{b}{{2{\rm{a}}}} = 1\)
Đáp án A. \(y = {x^2} + 2x – 2\) có \(a = 1,b = 2 \Rightarrow \frac{{ – b}}{{2a}} = – 1\) (Loại)
Đáp án B. \(y = {x^2} – 2x – 2\) có \(a = 1,b = – 2 \Rightarrow \frac{{ – b}}{{2a}} = 1\) (TM)
Đáp án C. \(y = {x^2} + 3x – 2\) có \(a = 1,b = 3 \Rightarrow \frac{{ – b}}{{2a}} = – \frac{3}{2}\) (Loại)
Chọn B.
Câu 26 (TH):
Hướng dẫn:
Tọa độ đỉnh của parabol \(y = a{x^2} + bx + c\) là \(I\left( { – \frac{b}{{2a}};\frac{{ – \Delta }}{{4a}}} \right)\)
Cách giải:
Đồ thị hàm số cắt trục tung tại điểm \(\left( {0\,\,;\,\, – 1} \right)\) nên \(c = – 1\).
Tọa độ đỉnh \(I\left( {1\,\,;\, – 3} \right)\), ta có phương trình: \(\left\{ \begin{array}{l} – \frac{b}{{2a}} = 1\\a{.1^2} + b.1 – 1 = – 3\end{array} \right.\) \( \Leftrightarrow \left\{ \begin{array}{l}2a + b = 0\\a + b = – 2\end{array} \right.\) \( \Leftrightarrow \left\{ \begin{array}{l}a = 2\\b = – 4\end{array} \right.\).
Vậy parabol cần tìm là: \(y = 2{x^2} – 4x – 1\).
Chọn D.
Câu 27 (TH):
Hướng dẫn:
Khoảng biến thiên, kí hiệu là R, là hiệu giữa giá trị lớn nhất và giá trị nhỏ nhất trong mẫu số liệu.
Cách giải:
Giá trị lớn nhất trong mẫu số liệu là 19.
Giá trị nhỏ nhất trong mẫu số liệu là 2.
Vậy khoảng biến thiên R = 19 – 2 = 17.
Chọn C.
Câu 28 (VD):
Hướng dẫn:
Sử dụng công thức \(n\left( {A \cup B \cup C} \right) = n\left( A \right) + n\left( B \right) + n\left( C \right) – n\left( {A \cap B} \right) – n\left( {B \cap C} \right) – n\left( {C \cap A} \right) + n\left( {A \cap B \cap C} \right)\).
Cách giải:
Gọi A là tập hợp các bạn đăng kí tiết mục tốp ca \( \Rightarrow n\left( A \right) = 7.\)
B là tập hợp các bạn đăng kí tiết mục múa \( \Rightarrow n\left( B \right) = 6.\)
C là tập hợp các bạn đăng kí tiết mục diễn kịch \( \Rightarrow n\left( C \right) = 8.\)
\( \Rightarrow A \cap B:\) tập hợp các bạn đăng kí cả 2 tiết mục tốp ca và múa \( \Rightarrow n\left( {A \cap B} \right) = 3.\)
\(A \cap C\): tập hợp các bạn đăng kí cả 2 tiết mục tốp ca và diễn kịch \( \Rightarrow n\left( {A \cap C} \right) = 4.\)
\(B \cap C\): tập hợp các bạn đăng kí cả 2 tiết mục múa và diễn kịch \( \Rightarrow n\left( {B \cap C} \right) = 2.\)
\(A \cap B \cap C\): tập hợp các bạn đăng kí cả 3 tiết mục tốp ca, múa và diễn kịch \( \Rightarrow n\left( {A \cap B \cap C} \right) = 1.\)
\(A \cup B \cup C\): tập hợp các bạn đăng kí ít nhất 1 tiết mục.
Ta có: \(n\left( {A \cup B \cup C} \right) = n\left( A \right) + n\left( B \right) + n\left( C \right) – n\left( {A \cap B} \right) – n\left( {B \cap C} \right) – n\left( {C \cap A} \right) + n\left( {A \cap B \cap C} \right)\)
\( \Rightarrow n\left( {A \cup B \cup C} \right) = 7 + 6 + 8 – 3 – 4 – 2 + 1 = 13.\)
Chọn B.
Câu 29 (TH):
Hướng dẫn:
Sử dụng hai vectơ bằng nhau, đưa về hai vectơ chung điểm đầu và cuối, sử dụng quy tắc ba điểm.
Cách giải:
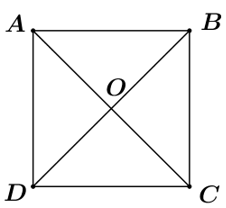
Ta có: \(\overrightarrow {AB} {\rm{ \;}} + \overrightarrow {OD} {\rm{ \;}} = \overrightarrow {OD} {\rm{ \;}} + \overrightarrow {AB} {\rm{ \;}} = \overrightarrow {OD} {\rm{ \;}} + \overrightarrow {DC} {\rm{ \;}} = \overrightarrow {OC} \).
\( \Rightarrow \left| {\overrightarrow {AB} {\rm{ \;}} + \overrightarrow {OD} } \right| = \left| {\overrightarrow {OC} } \right| = OC\).
Áp dụng định lí Pytago ta có:
\(AC = \sqrt {A{B^2} + B{C^2}} {\rm{ \;}} = \sqrt {{{\left( {4a} \right)}^2} + {{\left( {3a} \right)}^2}} {\rm{ \;}} = 5a \Rightarrow OC = \frac{1}{2}AC = \frac{5}{2}a.\)
Vậy \(\left| {\overrightarrow {AB} {\rm{ \;}} + \overrightarrow {OD} } \right| = OC = \frac{5}{2}a.\)
Chọn C.
Câu 30 (TH):
Hướng dẫn:
Sử dụng định nghĩa tích vô hướng của hai vectơ: \(\vec a.\vec b{\rm{ \;}} = \left| {\vec a} \right|.\left| {\vec b} \right|.\cos \left( {\vec a,\vec b} \right)\).
Cách giải:
Ta có:
\(\begin{array}{l}\vec a.\vec b = \left| {\vec a} \right|.\left| {\vec b} \right|.\cos \left( {\vec a,\vec b} \right)\\ \Leftrightarrow 2\vec a.\vec b = 2\left| {\vec a} \right|.\left| {\vec b} \right|.\cos \left( {\vec a,\vec b} \right)\\ \Leftrightarrow – \left| {\vec a} \right|.\left| {\vec b} \right| = 2\left| {\vec a} \right|.\left| {\vec b} \right|.\cos \left( {\vec a,\vec b} \right)\\ \Leftrightarrow \left| {\vec a} \right|.\left| {\vec b} \right|\left[ {1 + 2\cos \left( {\vec a,\vec b} \right)} \right] = 0\\ \Leftrightarrow \cos \left( {\vec a,\vec b} \right) = – \frac{1}{2}{\mkern 1mu} {\mkern 1mu} \left( {do{\mkern 1mu} {\mkern 1mu} \vec a \ne \vec 0,{\mkern 1mu} {\mkern 1mu} \vec b \ne \vec 0} \right)\end{array}\)
\( \Leftrightarrow \left( {\vec a,\vec b} \right) = {120^0}.\)
Chọn B.
Phần 2: Tự luận (4 điểm)
Câu 1 (VD):
Hướng dẫn:
a) Gọi I là trung điểm của BC. Chứng minh M là trung điểm của BI.
Sử dụng quy tắc ba điểm, công thức trung điểm.
b) Sử dụng điều kiện để hai vectơ cùng phương.
Cách giải:
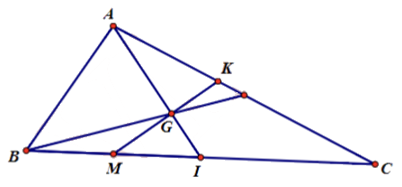
a) Gọi I là trung điểm của BC.
Ta có: \(3\overrightarrow {MB} {\rm{ \;}} + \overrightarrow {MC} {\rm{ \;}} = \vec 0{\rm{ \;}} \Rightarrow 3MB = MC \Rightarrow MB = \frac{1}{4}BC = \frac{1}{2}BI\).
=> M là trung điểm của BI.
Khi đó ta có:
\(\begin{array}{*{20}{l}}{\overrightarrow {MG} = \overrightarrow {MI} + \overrightarrow {IG} = \frac{1}{4}\overrightarrow {BC} – \frac{1}{3}\overrightarrow {AI} }\\{ = \frac{1}{4}\left( {\overrightarrow {AC} – \overrightarrow {AB} } \right) – \frac{1}{3}.\frac{1}{2}\left( {\overrightarrow {AB} + \overrightarrow {AC} } \right)}\\{ = \frac{1}{4}\overrightarrow {AC} – \frac{1}{4}\overrightarrow {AB} – \frac{1}{6}\overrightarrow {AB} – \frac{1}{6}\overrightarrow {AC} }\\{ = \frac{1}{{12}}\overrightarrow {AC} – \frac{5}{{12}}\overrightarrow {AB} {\mkern 1mu} {\mkern 1mu} \left( {dpcm} \right).}\end{array}\)
b) Đặt \(\overrightarrow {AK} {\rm{ \;}} = x\overrightarrow {AC} {\mkern 1mu} {\mkern 1mu} \left( {x > 0} \right)\), ta có:
\(\begin{array}{*{20}{l}}{\overrightarrow {GK} {\rm{ \;}} = \overrightarrow {AK} {\rm{ \;}} – \overrightarrow {AG} {\rm{ \;}} = x\overrightarrow {AC} {\rm{ \;}} – \frac{2}{3}\overrightarrow {AI} }\\{ = x\overrightarrow {AC} {\rm{ \;}} – \frac{2}{3}.\frac{1}{2}\left( {\overrightarrow {AB} {\rm{ \;}} + \overrightarrow {AC} } \right) = \left( {x – \frac{1}{3}} \right)\overrightarrow {AC} {\rm{ \;}} – \frac{1}{3}\overrightarrow {AB} }\end{array}\)
Vì M, G, K thẳng hàng nên \(\frac{{x – \frac{1}{3}}}{{\frac{1}{{12}}}} = \frac{{ – \frac{1}{3}}}{{ – \frac{5}{{12}}}} \Leftrightarrow x = \frac{2}{5}.\)
Vậy \(\overrightarrow {AK} {\rm{\;}} = \frac{2}{5}\overrightarrow {AC} \) nên \(AK = \frac{2}{5}AC \Rightarrow \frac{{KA}}{{KC}} = \frac{2}{3}.\)
Câu 2 (VD):
Hướng dẫn:
a) Hàm số \(y = a{x^2} + bx + c(a \ne 0)\) có đỉnh \(\left( { – \frac{b}{{2a}};\frac{{ – \Delta }}{{4a}}} \right)\).
b) Sự biến thiên
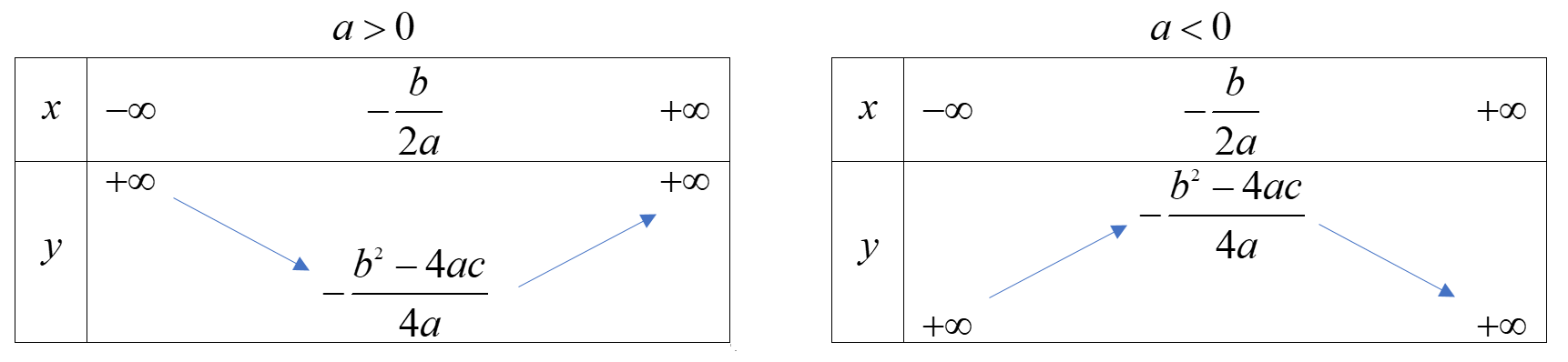
* Vẽ đồ thị
+ Đỉnh I\(\left( { – \frac{b}{{2a}};\frac{{ – \Delta }}{{4a}}} \right)\)
+ Trục đối xứng \(x = – \frac{b}{{2a}}\)
+ Giao với các trục (nếu có)
+ Lấy các điểm thuộc đồ thị (đối xứng nhau qua trục đối xứng).
Cách giải:
a) Ta có: (P) giao với Oy tại điểm có tung độ bằng -3 hay điểm (0;-3). Suy ra \(a.0 + b.0 + c = – 3 \Leftrightarrow c = – 3\)
Vì (P) có đỉnh I(2;-1) nên \(\left\{ \begin{array}{l}\frac{{ – b}}{{2a}} = 2\\a{.2^2} + b.2 + ( – 3) = – 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l} – b = 4a\\4a + 2b – 2 = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = – \frac{1}{2}\\b = 2\end{array} \right.\)
Vậy parabol (P) là \(y = – \frac{1}{2}{x^2} + 2x – 3\)
b) Hàm số \(y = – \frac{1}{2}{x^2} + 2x – 3\) có \(a = – \frac{1}{2} < 0\), đỉnh I(2;-1) nên có bảng biến thiên:
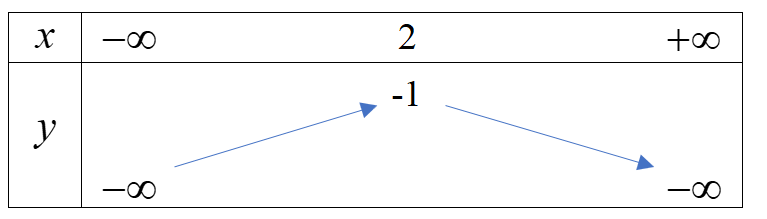
Hàm số đồng biến trên \(( – \infty ;2)\) và nghịch biến trên khoảng \((2; + \infty )\)
* Vẽ đồ thị
Đỉnh I(2;-1)
Trục đối xứng \(x = 2\)
Cắt trục tung tại A(0;-3) và không cắt Ox
Lấy B(4;-3) thuộc (P), đối xứng với A(0;-3) qua trục đối xứng
Lấy \(C\left( {1; – \frac{3}{2}} \right),D\left( {3; – \frac{3}{2}} \right)\) thuộc (P).
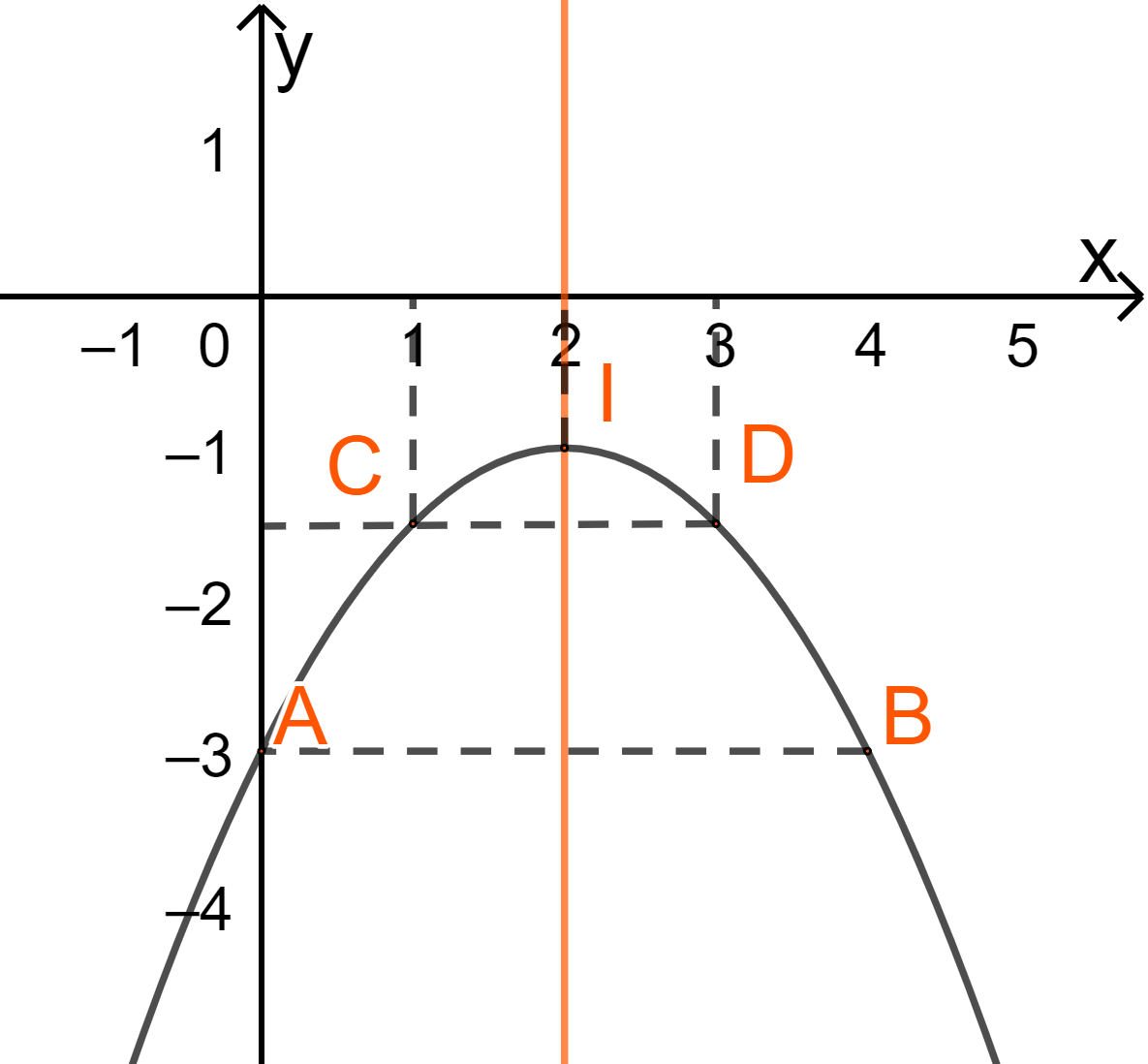
Câu 3 (VDC):
Hướng dẫn:
Ta thường dùng các chữ cái in hoa để kí hiệu tập hợp và chữ cái in thường để kí hiệu phần tử thuộc tập hợp.
Cách giải:
Ta có
\(\begin{array}{l}S = G{B^2} + G{C^2} + 9G{A^2}\\{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} = {\left( {\frac{2}{3}{m_b}} \right)^2} + {\left( {\frac{2}{3}{m_c}} \right)^2} + 9.{\left( {\frac{2}{3}{m_a}} \right)^2}\\{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} = \frac{4}{9}{m_b}^2 + \frac{4}{9}{m_c}^2 + 4{m_a}^2\\{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} = \frac{4}{9}.\left( {\frac{{2{a^2} + 2{c^2} – {b^2}}}{4} + \frac{{2{a^2} + 2{b^2} – {c^2}}}{4}} \right) + 4.\frac{{2{b^2} + 2{c^2} – {a^2}}}{4}\\{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} = \frac{4}{9}.\frac{{4{a^2} + {b^2} + {c^2}}}{4} + 2{b^2} + 2{c^2} – {a^2}\end{array}\)
\(\begin{array}{l}{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} = \frac{{4{a^2} + {b^2} + {c^2}}}{9} + 2{b^2} + 2{c^2} – {a^2}\\{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} = \frac{{19}}{9}\left( {{b^2} + {c^2}} \right) – \frac{5}{9}{a^2}\end{array}\)
Theo giả thiết ta có: \(4\sin A\tan A = \sin B\sin C \Leftrightarrow 4{\sin ^2}A = \sin B\sin C\cos A{\mkern 1mu} {\mkern 1mu} \left( * \right)\)
Áp dụng định lí sin trong tam giác ta có: \(\frac{a}{{\sin A}} = \frac{b}{{\sin B}} = \frac{c}{{\sin C}} = 2R \Rightarrow \left\{ {\begin{array}{*{20}{l}}{\sin A = \frac{a}{{2R}}}\\{\sin B = \frac{b}{{2R}}}\\{\sin C = \frac{c}{{2R}}}\end{array}} \right.\)
Thay vào (*) ta có:
\(\begin{array}{*{20}{l}}{\left( * \right) \Leftrightarrow 4{{\left( {\frac{a}{{2R}}} \right)}^2} = \frac{b}{{2R}}.\frac{c}{{2R}}\cos A}\\{{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} \Leftrightarrow 4.\frac{{{a^2}}}{{4{R^2}}} = \frac{{bc}}{{4{R^2}}}\cos A}\\{{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} \Leftrightarrow 4{a^2} = bc\cos A}\end{array}\)
Lại theo định lí cosin trong tam giác ABC ta có:
\(\begin{array}{*{20}{l}}{{a^2} = {b^2} + {c^2} – 2bc\cos A}\\{ \Rightarrow bc\cos A = \frac{{{b^2} + {c^2} – {a^2}}}{2}}\end{array}\)
Khi đó ta có:
\(\begin{array}{*{20}{l}}{\left( * \right) \Leftrightarrow 4{a^2} = \frac{{{b^2} + {c^2} – {a^2}}}{2}}\\{ \Leftrightarrow 8{a^2} = {b^2} + {c^2} – {a^2}}\\{ \Leftrightarrow 9{a^2} = {b^2} + {c^2}}\end{array}\)
Do đó: \(S = \frac{{19}}{9}\left( {{b^2} + {c^2}} \right) – \frac{5}{9}{a^2} = \frac{{19}}{9}.9{a^2} – \frac{5}{9}{a^2} = \frac{{166{a^2}}}{9} = 166.\)
Vậy S = 166.