Đáp án Lời giải Đề thi học kì 1 Toán 10 – Đề số 4 – Đề thi đề kiểm tra Toán lớp 10 Chân trời sáng tạo.
Câu hỏi/Đề bài:
HƯỚNG DẪN CHI TIẾT
I. Phần trắc nghiệm (6 điểm – 30 câu)
|
1.C |
2.C |
3.D |
4.D |
5.A |
6.B |
7.C |
8.C |
9.B |
10.C |
|
11.A |
12.C |
13.C |
14.C |
15.C |
16.A |
17.D |
18.A |
19.D |
20.A |
|
21.D |
22.C |
23.B |
24.B |
25.D |
26.B |
27.B |
28.D |
29.B |
30.D |
Câu 1 (TH):
Cách giải:
\(P\left( 3 \right):\) là mệnh đề sai.
\(P\left( 4 \right):\) là mệnh đề sai.
\(P\left( 1 \right):\) là mệnh đề sai.
\(P\left( 5 \right):\) là mệnh đề đúng.
Chọn D.
Câu 2 (TH):
Hướng dẫn:
Phủ định của \(\forall \) là \(\exists \), phủ định của < là \( \ge \)
Cách giải:
Phủ định của \(\forall x \in R,{x^2} – x + 7 < 0\) là \(\exists x \in R,{x^2} – x + 7 \ge 0\).
Chọn A.
Câu 3 (NB):
Hướng dẫn:
\(X \subset Y \Leftrightarrow \forall x \in X \Rightarrow x \in Y\)
Cách giải:
Ta có \(A \subset X\) nên \(X\) có ít nhất \(3\) phần tử \(\left\{ {1;2;3} \right\}.\)
Ta có \(X \subset B\) nên \(X\) phải \(X\) có nhiều nhất \(5\) phần tử và các phần tử thuộc \(X\) cũng thuộc \(B.\)
Do đó các tập \(X\) thỏa mãn là có \(4\) tập thỏa mãn.
Chọn A.
Câu 4 (TH):
Hướng dẫn:
Giải phương trình \(\left( {{x^2} – x – 6} \right)\left( {{x^2} – 5} \right) = 0\) và lấy các nghiệm hữu tỉ.
Cách giải:
Ta có \(\left( {{x^2} – x – 6} \right)\left( {{x^2} – 5} \right) = 0 \Leftrightarrow \left[ \begin{array}{l}{x^2} – x – 6 = 0\\{x^2} – 5 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 3 \in \mathbb{Q}\\x = – 2 \in \mathbb{Q}\\x = \sqrt 5 \notin \mathbb{Q}\\x = – \sqrt 5 \notin \mathbb{Q}\end{array} \right.\).
Do đó \(X = \left\{ { – 2;3} \right\}\).
Chọn C.
Câu 5 (TH):
Hướng dẫn:
Áp dụng định nghĩa tìm các phép toán trên tập hợp.
Cách giải:
Ta có \(\left\{ \begin{array}{l}A\backslash B = \left\{ {0;1} \right\}\\B\backslash A = \left\{ {5;6} \right\}\end{array} \right. \Rightarrow \left( {A\backslash B} \right) \cap \left( {B\backslash A} \right) = \emptyset \).
Chọn D.
Câu 6 (TH): –
Hướng dẫn:
Biểu diễn các tập hợp trên trục số và áp dụng định nghĩa các phép toán trên tập hợp.
Cách giải:
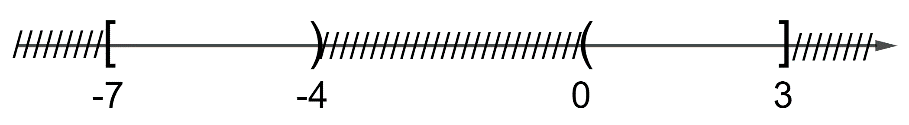
\([ – 7;3]{\rm{\backslash }}[ – 4;0] = [ – 7; – 4) \cup (0;3]\)
Chọn B.
Câu 7 (NB):
Hướng dẫn:
Thay tọa độ các điểm vào bất phương trình và kiểm tra tính đúng sai.
Cách giải:
Ta có \(3x + 2\left( {y + 3} \right) > 4\left( {x + 1} \right) – y + 3\, \Leftrightarrow \, – x + 3y – 1 > 0\).
Vì \( – 2 + 3.1 – 1 > 0\) là mệnh đề đúng nên miền nghiệm của bất phương trình trên chứa điểm có tọa độ \(B\).
Chọn C.
Câu 8 (TH):
Hướng dẫn:
Thay tọa độ các điểm vào bất phương trình và kiểm tra tính đúng sai
Cách giải:
Ta thay lần lượt tọa độ các điểm vào hệ bất phương trình.
Với \(M\left( {0;1} \right) \Rightarrow \)\(\left\{ \begin{array}{l}0 + 3.1 – 2 \ge 0\\2.0 + 1 + 1 \le 0\end{array} \right.\). Bất phương trình thứ hai sai nên A sai.
Với \(N\left( {–1;1} \right) \Rightarrow \)\(\left\{ \begin{array}{l} – 1 + 3.1 – 2 \ge 0\\2.\left( { – 1} \right) + 1 + 1 \le 0\end{array} \right.\): Đúng.
Chọn B.
Câu 9 (NB):
Hướng dẫn:
Mốt là gía trị có tần số lớn nhất trong mẫu.
Cách giải:
Tiền thưởng 4 triệu đồng được thưởng cho 15 người \( \Rightarrow {M_0} = 4\)
Chọn A.
Câu 10 (TH):
Hướng dẫn:
Tần suất \({f_i}\)của giá trị \({x_i}\) là tỉ số giữa tần số n và kích thước mẫu N có công thức \({f_i} = \frac{n}{N}\).
Cách giải:
Tần suất \(f = \frac{{10}}{{380}} = \frac{1}{{38}} \approx 2,63\% \)
Chọn A.
Câu 11 (TH):
Hướng dẫn:
Số trung bình là \(\overline x = \frac{{{x_1} + {x_2} + {x_3} + … + {x_n}}}{n}\)
Cách giải:
Tiền thưởng trung bình:
\(\overline x = \frac{{5.2 + 15.3 + 10.4 + 6.5 + 4.6}}{{40}}\)
\(\overline x = 3,725\) (triệu đồng)
Chọn A.
Câu 12 (TH):
Hướng dẫn:
Các giá trị xuất hiện nhiều nhất trong mẫu số liệu được gọi là mốt
Cách giải:
Chọn C.
Câu 13 (TH):
Hướng dẫn:
Bước 1: Sắp thứ tự các số liệu thống kê thành 1 dãy không giảm (không tăng).
Bước 2:
+ Nếu số phần tử lẻ thì \({M_e}\) là số đứng giữa dãy.
+ Nếu số phần tử chẵn thì \({M_e}\) là trung bình cộng của 2 số đứng giữa dãy.
Cách giải:
Sắp thứ tự các số liệu thống kê thành một dãy không giảm là:
1 4 4 6 7 9 10
Vậy số trung vị là \({M_e} = 6\)
Chọn B.
Câu 14 (TH):
Hướng dẫn:
Dùng MTCT để tính
Cách giải:
+ Điểm trung bình của 100 học sinh là: \(\overline x = 15,09\)
+ Độ lệch chuẩn:
\(S = \sqrt \begin{array}{l}\frac{1}{{100}}\left[ {2.{{\left( {9 – 15,09} \right)}^2} + 1.{{\left( {10 – 15,09} \right)}^2}} \right.\\ & \left. { + … + 3.{{\left( {19 – 15,09} \right)}^2}} \right]\end{array} \)
\(S \approx 2,17\)
Chọn D.
Câu 15 (NB):
Hướng dẫn:
Hàm phân thức xác định khi mẫu thức khác 0.
Cách giải:
Hàm số xác định khi và chỉ khi \({x^2} + 3x – 4 \ne 0 \Leftrightarrow \left\{ \begin{array}{l}x \ne 1\\x \ne – 4\end{array} \right.\)
Vậy TXĐ của hàm số là \(D = \mathbb{R}\backslash \left\{ {1; – 4} \right\}\).
Chọn B.
Câu 16 (TH):
Hướng dẫn:
Căn bậc 2 xác định khi biểu thức trong căn không âm.
Cách giải:
ĐKXĐ: \(\left\{ \begin{array}{l}6 – 3x \ge 0\\x + 2 \ge 0\\x \ne 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x \le 2\\x \ge – 2\\x \ne 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l} – 2 \le x \le 2\\x \ne 0\end{array} \right.\).
Vậy TXĐ của hàm số là \({\rm{D}} = \left[ { – 2;2} \right]{\rm{\backslash }}\{ 0\} .\).
Chọn C.
Câu 17 (TH):
Cách giải:
TXĐ: \({\rm{D}} = \mathbb{R}\). Với mọi \({x_1},{x_2} \in \mathbb{R}\) và \({x_1} < {x_2}\), ta có
\(f\left( {{x_1}} \right) – f\left( {{x_2}} \right) = \left( {4 – 3{x_1}} \right) – \left( {4 – 3{x_2}} \right) = – 3\left( {{x_1} – {x_2}} \right) > 0.\)
Suy ra \(f\left( {{x_1}} \right) > f\left( {{x_2}} \right)\). Do đó, hàm số nghịch biến trên \(\mathbb{R}\).
Mà \(\left( {\frac{4}{3}; + \infty } \right) \subset \mathbb{R}\) nên hàm số cũng nghịch biến trên \(\left( {\frac{4}{3}; + \infty } \right)\).
Chọn B.
Câu 18 (TH):
Hướng dẫn:
Thay tọa độ các điểm ở các đáp án vào hàm số. Điểm nào thỏa mãn hàm số thì sẽ thuộc đồ thị hàm số.
Cách giải:
Thay \(x = 2\) vào hàm số ta được: \(y = \frac{{\sqrt {2 – 2} – 2}}{{2 – 6}} = \frac{{ – 2}}{{ – 4}} = 0,5\) nên điểm \((2;0,5)\) thuộc đồ thị hàm số.
Chọn C.
Câu 19 (VD):
Hướng dẫn:
Phân tích biêu thức về dạng có hằng đẳng thức
Cách giải:
\(D = [3; + \infty )\)
\(y = x – 2\sqrt {x – 3} = \left( {x – 3 – 2\sqrt {x – 3} + 1} \right) + 2 = {\left( {\sqrt {x – 3} – 1} \right)^2} + 2 \ge 2\) khi x = 4.
Chọn D.
Câu 20 (NB):
Hướng dẫn:
Cho hàm số bậc hai \(y = a{x^2} + bx + c\) \(\left( {a \ne 0} \right)\) có đồ thị \(\left( P \right)\), đỉnh của \(\left( P \right)\) là \(I\left( { – \frac{b}{{2a}};\; – \;\frac{\Delta }{{4a}}} \right)\)
Cách giải:
Tọa độ đỉnh của parabol \(y = – 2{x^2} – 4x + 6\) là \(\left\{ \begin{array}{l}x = – \frac{{ – 4}}{{2.\left( { – 2} \right)}} = – 1\\y = – 2.{\left( { – 1} \right)^2} – 4.\left( { – 1} \right) + 6 = 8\end{array} \right. \Rightarrow I\left( { – 1;8} \right)\).
Chọn A.
Câu 21 (NB):
Hướng dẫn:
Dùng bảng các giá trị lượng giác đặc biệt.
Cách giải:
Tra bảng giá trị lượng giác của các góc đặc biệt, ta được
\(\sin {30^ \circ } = \cos {60^ \circ } = \frac{1}{2};\sin {60^ \circ } = \cos {30^ \circ } = \frac{{\sqrt 3 }}{2}.\)
\( \Rightarrow P = \frac{1}{2}.\frac{1}{2} + \frac{{\sqrt 3 }}{2}.\frac{{\sqrt 3 }}{2} = 1\)
Chọn A.
Chọn D.
Câu 22 (NB):
Hướng dẫn:
Dùng định lý cosin \({b^2} = {a^2} + {c^2} – 2ac.\cos B\)
Cách giải:
Theo định lí hàm sin, ta có \(\frac{{AB}}{{\sin C}} = \frac{{AC}}{{\sin B}} \Leftrightarrow \frac{5}{{\sin {{45}^ \circ }}} = \frac{{AC}}{{\sin {{60}^ \circ }}} \Rightarrow AC = \frac{{5\sqrt 6 }}{2}\)
Chọn A.
Câu 23 (TH):
Hướng dẫn:
Dùng định lý cosin \(\cos A = \frac{{{b^2} + {c^2} – {a^2}}}{{2bc}}\)
Cách giải:
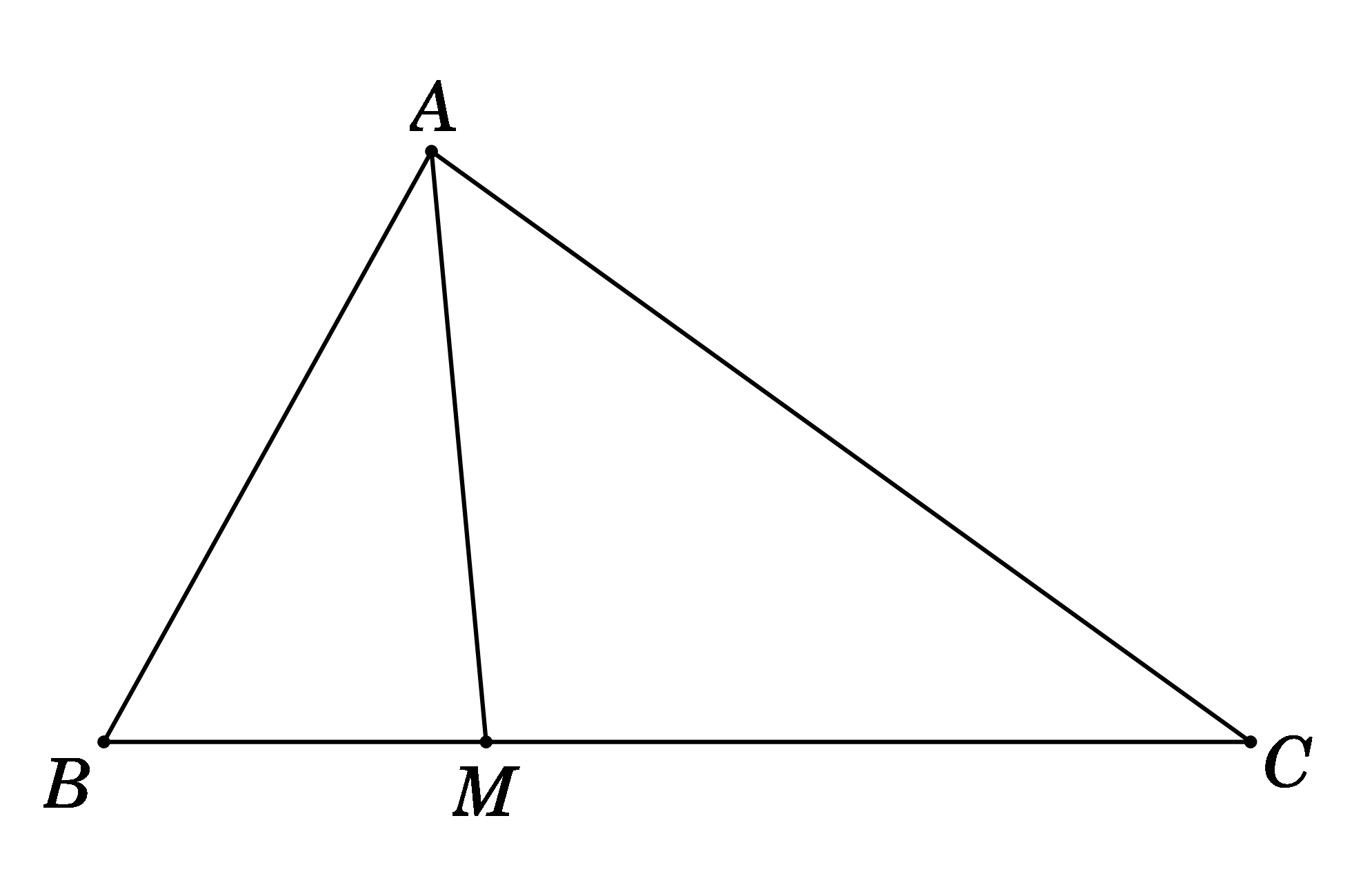
Theo định lí hàm cosin, ta có: \(\cos B = \frac{{A{B^2} + B{C^2} – A{C^2}}}{{2AB.BC}} = \frac{{{4^2} + {6^2} – {{\left( {2\sqrt 7 } \right)}^2}}}{{2.4.6}} = \frac{1}{2}\)
Do \(MC = 2MB \Rightarrow BM = \frac{1}{3}BC = 2\)
Theo định lí hàm cosin, ta có
\(\begin{array}{l}A{M^2} = A{B^2} + B{M^2} – 2.AB.BM.\cos B\\ = {4^2} + {2^2} – 2.4.2.\frac{1}{2} = 12\\ \Rightarrow AM = 2\sqrt 3 \end{array}\)
Chọn C.
Câu 24 (TH):
Hướng dẫn:
Tính \(\angle C = {180^0} – \left( {\angle A + \angle B} \right)\).
Sử dụng định lí sin: \(\frac{c}{{\sin C}} = 2R\).
Cách giải:
Ta có: \(\angle C = {180^0} – \left( {\angle A + \angle B} \right) = {60^0}\).
Áp dụng định lí sin ta có: \(\frac{c}{{\sin C}} = 2R \Rightarrow R = \frac{c}{{2\sin C}} = \frac{6}{{2\sin {{60}^0}}} = 2\sqrt 3 \).
Chọn B.
Câu 25 (TH):
Hướng dẫn:
Áp dụng quy tắc cộng vecto, quy tắc hình bình hành để biểu diễn véctơ.
Cách giải:
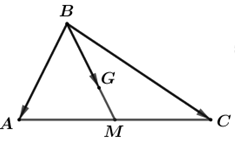
\(\overrightarrow {BM} {\rm{\;}} = \frac{1}{2}\left( {\overrightarrow {BA} {\rm{\;}} + \overrightarrow {BC} } \right) = \frac{1}{2}\overrightarrow {BA} {\rm{\;}} + \frac{1}{2}\overrightarrow {BC} \)
\( \Rightarrow \overrightarrow {BG} {\rm{\;}} = \frac{2}{3}\overrightarrow {BM} {\rm{\;}} = \frac{2}{3} \cdot \left( {\frac{1}{2}\overrightarrow {BA} {\rm{\;}} + \frac{1}{2}\overrightarrow {BC} } \right) = \frac{1}{3}\overrightarrow {BA} {\rm{\;}} + \frac{1}{3}\overrightarrow {BC} \)
Mặt khác, \(\overrightarrow {BA} {\rm{\;}} = \vec a,{\mkern 1mu} {\mkern 1mu} \overrightarrow {BC} {\rm{\;}} = \vec b\) nên ta có: \(\overrightarrow {BG} {\rm{\;}} = \frac{1}{3}\vec a + \frac{1}{3}\vec b\)
Vậy \(\overrightarrow {BG} {\rm{\;}} = \frac{1}{3}\vec a + \frac{1}{3}\vec b\).
Chọn A.
Câu 26 (TH):
Hướng dẫn:
Dùng quy tắc cộng, trừ hai vecto
Cách giải:
Xét các đáp án:
Ÿ Đáp án A. Ta có \(\overrightarrow {AB} + \overrightarrow {BC} + \overrightarrow {CA} = \overrightarrow {AA} = \overrightarrow 0 .\)
Ÿ Đáp án B. Ta có \(\overrightarrow {AP} + \overrightarrow {BM} + \overrightarrow {CN} = \frac{1}{2}\overrightarrow {AB} + \frac{1}{2}\overrightarrow {BC} + \frac{1}{2}\overrightarrow {CA} \)
\( = \frac{1}{2}\left( {\overrightarrow {AB} + \overrightarrow {BC} + \overrightarrow {CA} } \right) = \frac{1}{2}\overrightarrow {AA} = \overrightarrow 0 .\)
Ÿ Đáp án C. Ta có \(\overrightarrow {MN} + \overrightarrow {NP} + \overrightarrow {PM} = \overrightarrow {MM} = \overrightarrow 0 .\)
Ÿ Đáp án D. Ta có \(\overrightarrow {PB} + \overrightarrow {MC} = \frac{1}{2}\overrightarrow {AB} + \frac{1}{2}\overrightarrow {BC} = \frac{1}{2}\overrightarrow {AC} = \overrightarrow {AN} = \overrightarrow {PM} = – \overrightarrow {MP} .\)
Chọn D.
Câu 27 (VD):
Hướng dẫn:
Dùng quy tắc cộng, trừ hai vecto
Cách giải:
Ta có \(\overrightarrow {OB} – \overrightarrow {OC} = \overrightarrow {CB} = \overrightarrow {DA} \).
Chọn B.
Câu 28 (VD):
Hướng dẫn:
Nếu M là trung điểm của AB thì với mọi điểm O là luôn có \(\overrightarrow {OA} + \overrightarrow {OB} = 2\overrightarrow {OM} \)
Cách giải:
Gọi \(M\) là trung điểm \(BC \Rightarrow AM \bot BC.\)
Trong tam giác vuông \(AMB\), ta có \(AM = AB.\sin \widehat {ABM} = a.\sin {30^0} = \frac{a}{2}.\)

Ta có \(\left| {\overrightarrow {AB} + \overrightarrow {AC} } \right| = \left| {2\overrightarrow {AM} } \right| = 2AM = a.\)
Chọn B.
Câu 29:
Hướng dẫn:
\(\overrightarrow a .\overrightarrow b = \left| {\overrightarrow a } \right|.\left| {\overrightarrow b } \right|.\cos \left( {\overrightarrow a ,\,\overrightarrow b } \right)\)
Cách giải:
Ta có \(\left( {\overrightarrow {AB} ,\overrightarrow {AC} } \right) = \widehat {BAC} = {45^ \circ }\) nên \(\overrightarrow {AB} .\overrightarrow {AC} = AB.AC.\cos {45^ \circ } = a.a\sqrt 2 .\frac{{\sqrt 2 }}{2} = {a^2}\)
Chọn A.
Câu 30 (TH):
Hướng dẫn:
Cách giải:
Ta có \(\left| {\overrightarrow {AB} – \overrightarrow {DA} } \right| = \left| {\overrightarrow {AB} + \overrightarrow {AD} } \right| = \left| {\overrightarrow {AC} } \right| = AC = a\sqrt 2 .\)
Chọn C.
II. Phần tự luận (4 điểm)
Câu 1 (VD):
Hướng dẫn:
Dùng các phép toán trên tập hợp
Cách giải:
Gọi tập hợp các học sinh thích môn Toán là A. Khi đó n(A)=20
Gọi tập hợp các học sinh thích môn Anh là B. Khi đó n(B)=18
Số học sinh học thích môn Toán hoặc thích môn Anh là \(n\left( {A \cup B} \right)\) là 40 – 12 = 28 học sinh
Vậy số học sinh thích môn cả 2 môn Toán, Anh là \(n\left( {A \cap B} \right) = n\left( A \right) + n\left( B \right) – n\left( {A \cup B} \right) = 20 + 18 – 28 = 10\)
Vậy có tất cả 10 học sinh vừa thích môn Toán vừa thích môn Anh.
Câu 2 (VD):
Hướng dẫn:
a) Hàm số \(y = a{x^2} + bx + c(a \ne 0)\) có trục đối xứng \(x = – \frac{b}{{2a}}\).
b) Sự biến thiên
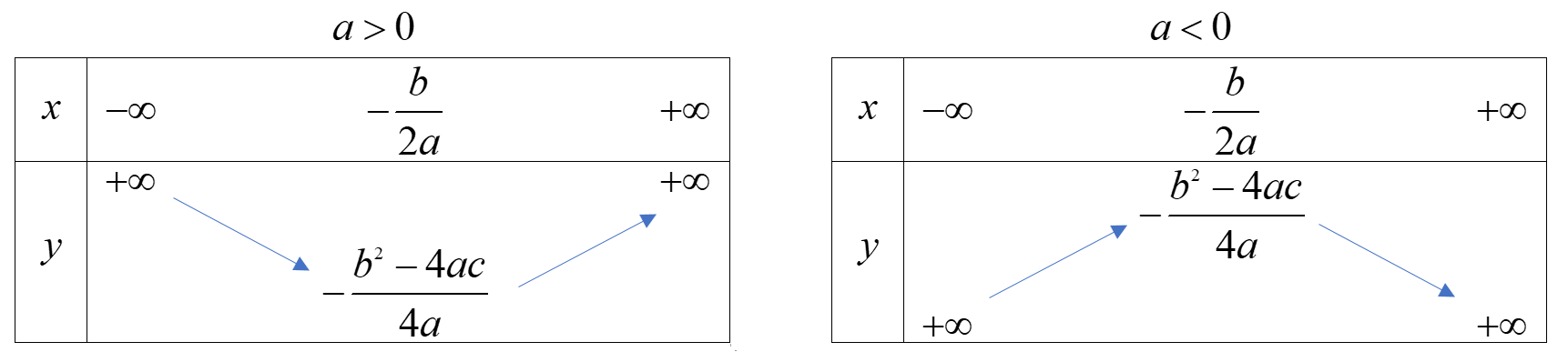
* Vẽ đồ thị
+ Đỉnh I\(\left( { – \frac{b}{{2a}};\frac{{ – \Delta }}{{4a}}} \right)\)
+ Trục đối xứng \(x = – \frac{b}{{2a}}\)
+ Giao với các trục (nếu có)
+ Lấy các điểm thuộc đồ thị (đối xứng nhau qua trục đối xứng).
Cách giải:
a. Hàm số \(\left( P \right):y = 2{x^2} + bx + c,\) có \(a = 2\)
Ta có \(M(0;4) \in (P)\) suy ra \(4 = {2.0^2} + b.0 + c \Leftrightarrow c = 4\)
Mà (P) có trục đối xứng \(x = 1\). Do đó \( – \frac{b}{{2a}} = 1 \Leftrightarrow b = – 2a = – 2.2 = – 4\)
Vậy hàm số có dạng \(y = 2{x^2} – 4x + 4\)
b. \(y = 2{x^2} – 4x + 4\)
Đỉnh S có tọa độ \(x = – \frac{{ – 4}}{{2.2}} = 1\), \(y = {2.1^2} – 4.1 + 4 = 2\)
Vì hàm số có a = 2 > 0 nên ta có bảng biến thiên
Vậy hàm số đồng biến trên \((1; + \infty )\), nghịch biến trên \(( – \infty ;1)\).
* Đồ thị:
Trong mặt phẳng Oxy đồ thị của \(y = 2{x^2} – 4x + 4\)là parabol (P) có:
Đỉnh I (1;2)
Trục đối xứng là x = 1
Bề lõm quay lên trên
Cắt trục tung tại điểm A(0,4)
Lấy điểm B(2;4) đối xứng với A qua trục đối xứng.
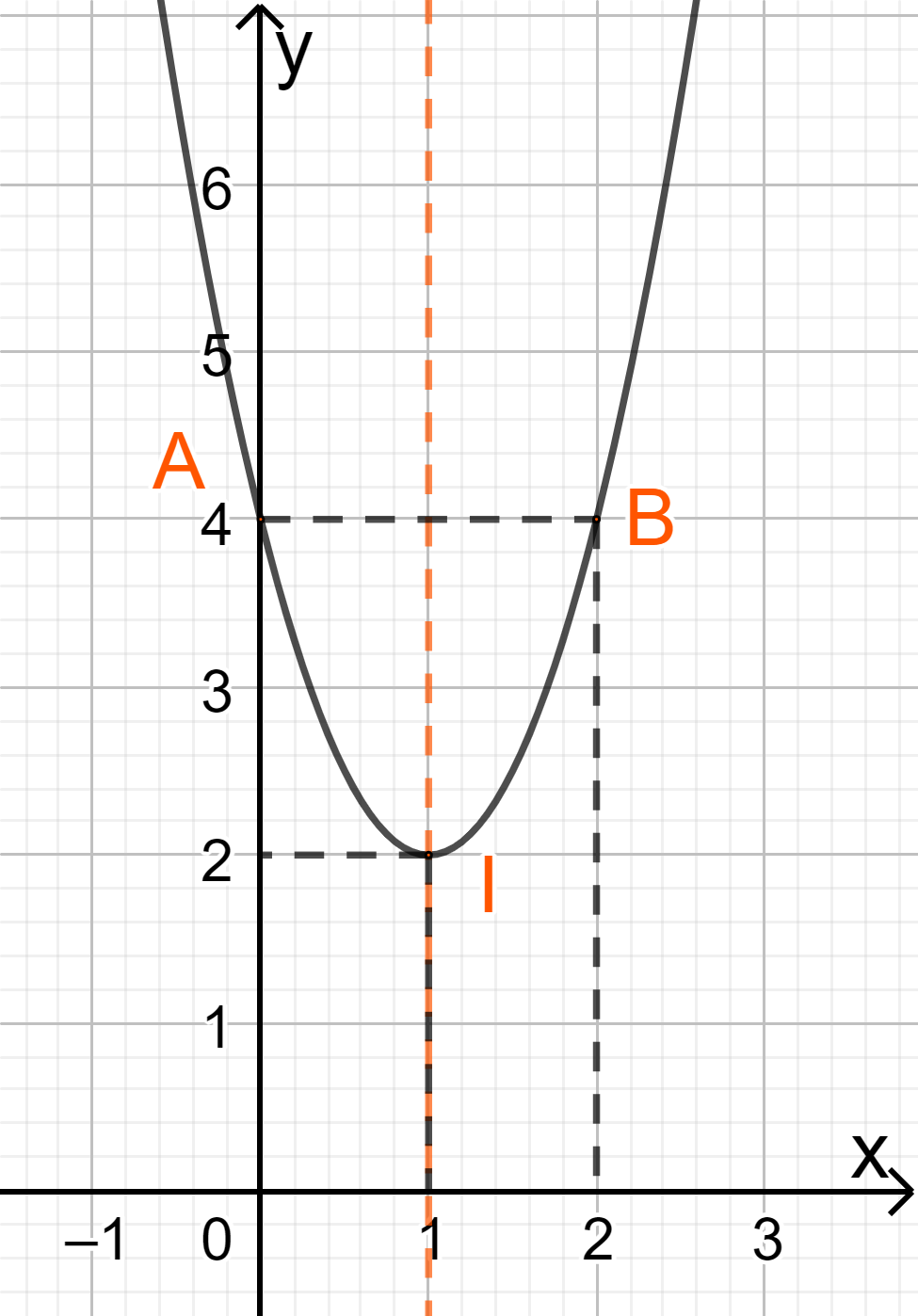
Câu 3 (TH):
Hướng dẫn:
Áp dụng định lí sin.
Cách giải:
Gọi D là đỉnh tháp, C là điểm chính giữa của chân tháp. Khi đó chiều cao của tháp là CD.

Ta có: \(\widehat {CAD} = {63^o},\widehat {CBD} = {48^o} \Rightarrow \widehat {DAB} = {180^o} – \widehat {CAD} = {180^o} – {63^o} = {117^o}\)
Xét tam giác DAB ta có: \(AB = 100,\widehat A = {117^o},\widehat B = {48^o}\)\( \Rightarrow \widehat {ADB} = {180^ \circ } – {117^ \circ } – {48^ \circ } = {15^ \circ }\)
Áp dụng định lí sin ta được: \(\frac{{AB}}{{\sin \widehat {ADB}}} = \frac{{DB}}{{\sin \widehat {DAB}}} \Leftrightarrow \frac{{100}}{{\sin {{15}^ \circ }}} = \frac{{DB}}{{\sin {{117}^ \circ }}}\)
\( \Rightarrow DB = \sin {117^ \circ }.\frac{{100}}{{\sin {{15}^ \circ }}}\)
Lại có: \(\Delta DCB\) vuông tại C, suy ra \(CD = DB.\sin B\)
\( \Leftrightarrow CD = \sin {117^ \circ }.\frac{{100}}{{\sin {{15}^ \circ }}}.\sin {48^ \circ } \approx 256\)
Vậy tháp đó cao khoảng 256m.
Câu 4 (VD):
Hướng dẫn:
Nếu M là trung điểm của AB thì với mọi điểm O ta luôn có \(\overrightarrow {OA} + \overrightarrow {OB} = 2\overrightarrow {OM} \)
Cách giải:
a) Ta có: \(\overrightarrow {AK} = \frac{1}{2}(\overrightarrow {AM} + \overrightarrow {AN} )\) (vì \(K\) là trung điểm của \(\left. {MN} \right)\)
Mà M là trung điểm AB, suy ra \(\overrightarrow {AM} = \frac{1}{2}\overrightarrow {AB} \)
Lại có: \(NA = \frac{1}{2}NC \Rightarrow AN = \frac{1}{3}AC \Rightarrow \overrightarrow {AN} = \frac{1}{3}\overrightarrow {AC} \)
\( \Rightarrow \overrightarrow {AK} = \frac{1}{2}\left( {\frac{1}{2}\overrightarrow {AB} + \frac{1}{3}\overrightarrow {AC} } \right)\) \( = \frac{1}{4}\overrightarrow {AB} + \frac{1}{6}\overrightarrow {AC} \)
b) Ta có: \(\overrightarrow {KD} = \frac{1}{2}(\overrightarrow {KB} + \overrightarrow {KC} )\) (do D là trung điểm BC)
\( = \frac{1}{2}(\overrightarrow {KA} + \overrightarrow {AB} + \overrightarrow {KA} + \overrightarrow {AC} ) = \overrightarrow {KA} + \frac{1}{2}\overrightarrow {AB} + \frac{1}{2}\overrightarrow {AC} \) \( = – \overrightarrow {AK} + \frac{1}{2}\overrightarrow {AB} + \frac{1}{2}\overrightarrow {AC} \)
\( = – \frac{1}{4}\overrightarrow {AB} – \frac{1}{6}\overrightarrow {AC} + \frac{1}{2}\overrightarrow {AB} + \frac{1}{2}\overrightarrow {AC} = \frac{1}{4}\overrightarrow {AB} + \frac{1}{3}\overrightarrow {AC} \) (đpcm)