Giải Lời giải Đề thi học kì 1 Toán 10 – Đề số 10 – Đề thi đề kiểm tra Toán lớp 10 Chân trời sáng tạo.
Câu hỏi/Đề bài:
HƯỚNG DẪN GIẢI CHI TIẾT
Phần 1: Trắc nghiệm (30 câu – 6 điểm)
|
1.B |
2.D |
3.C |
4.B |
5.C |
6.C |
7.C |
8.B |
9.B |
10.D |
|
11.A |
12.A |
13.A |
14.B |
15.C |
16.B |
17.C |
18.A |
19.C |
20.C |
|
21.D |
22.D |
23.A |
24.D |
25.A |
26.C |
27.A |
28.C |
29.B |
30.C |
Câu 1 (NB):
Hướng dẫn:
Mệnh đề là câu khẳng định có tính đúng hoặc sai.
Cách giải:
Các câu c), f), g) không phải là mệnh đề
Chọn C.
Câu 2 (TH):
Cách giải:
\(\bar a = 17658\,\, \pm \,\,16 \Rightarrow d = 16\)
Hàng lớn nhất của d là hàng chục nên ta làm tròn số \(a = 17658\) đến hàng trăm, kết quả là: \(17700.\)
Chọn A.
Câu 3 (TH):
Hướng dẫn:
Sử dụng tính chất trung điểm: \(\overrightarrow {OA} + \overrightarrow {OB} = \overrightarrow 0 \) với O là trung điểm của AB.
Sử dụng quy tắc hình bình hành \(\overrightarrow {AB} + \overrightarrow {AD} = \overrightarrow {AC} \)
Cách giải:

Xét các đáp án:
Ÿ Đáp án A. Ta có \(\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} + \overrightarrow {OD} = \left( {\overrightarrow {OA} + \overrightarrow {OC} } \right) + \left( {\overrightarrow {OB} + \overrightarrow {OD} } \right) = \vec 0.\)
Ÿ Đáp án B. Ta có \(\overrightarrow {AB} + \overrightarrow {AD} = \overrightarrow {AC} \) (quy tắc hình bình hành).
Ÿ Đáp án C. Ta có \(\left\{ \begin{array}{l}\left| {\overrightarrow {BA} + \overrightarrow {BC} } \right| = \left| {\overrightarrow {BD} } \right| = BD\\\left| {\overrightarrow {DA} + \overrightarrow {DC} } \right| = \left| {\overrightarrow {DB} } \right| = BD\end{array} \right.\).
Ÿ Đáp án D. Do \(\overrightarrow {CD} \ne \overrightarrow {CB} \Rightarrow \left( {\overrightarrow {AB} + \overrightarrow {CD} } \right) \ne \left( {\overrightarrow {AB} + \overrightarrow {CB} } \right).\)
Chọn D.
Câu 4 (TH):
Cách giải:
Ta dùng biểu đồ Ven để giải:
Gọi A là tập hợp các học sinh giỏi Toán của lớp 10E
B là tập hợp các học sinh giỏi Lý của lớp 10E
C là tập hợp các học sinh giỏi Hóa của lớp 10E
\( \Rightarrow n(A) = 7;n(B) = 5;n(6)\)
Hơn nữa \(n(A \cap B) = 3;n(A \cap C) = 4;n(B \cap C) = 2;n(A \cap B \cap C) = 1\)
Số học sinh giỏi Toán và Lý mà không giỏi Hóa là: \(3 – 1 = 2\) (học sinh)
Số học sinh giỏi Toán và Hóa mà không giỏi Lý là: \(4 – 1 = 3\) (học sinh)
Số học sinh giỏi Lý và Hóa mà không giỏi Toán là: \(2 – 1 = 1\) (học sinh)
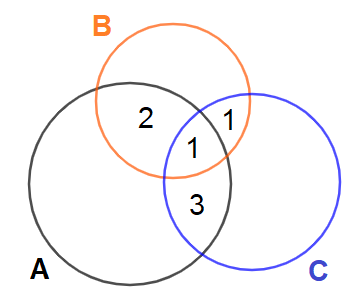
Số học sinh chỉ giỏi Toán là: \(7 – 2 – 1 – 3 = 1\) (học sinh)
Số học sinh chỉ giỏi Lí là: \(5 – 2 – 1 – 1 = 1\) (học sinh)
Số học sinh chỉ giỏi Hóa là: \(6 – 3 – 1 – 1 = 1\) (học sinh)
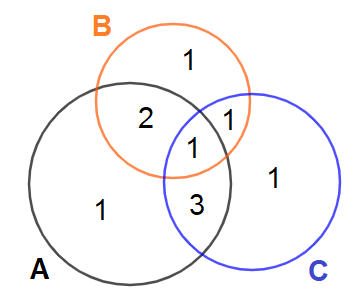
Nhìn vào biểu đồ, số học sinh giỏi ít nhất \(1\) trong \(3\) môn là: \(1 + 2 + 1 + 3 + 1 + 1 + 1 = 10\)
Chọn B.
Câu 5 (TH):
Cách giải:
Ta có \(3x + 2\left( {y + 3} \right) > 4\left( {x + 1} \right) – y + 3\, \Leftrightarrow \, – x + 3y – 1 > 0\).
Vì \( – 2 + 3.1 – 1 > 0\) là mệnh đề đúng nên miền nghiệm của bất phương trình trên chứa điểm có tọa độ \(B\).
Chọn C.
Câu 6 (TH):
Cách giải:
Do miền nghiệm không chứa biên nên ta loại đáp án A và C.
Chọn điểm \(M\left( {0;1} \right)\)thử vào các hệ bất phương trình.
Xét đáp án B, ta có \(\left\{ \begin{array}{l}0 – 2.1 > 0\\0 + 3.1 < – 2\end{array} \right.\): Sai.
Chọn D.
Câu 7 (VD):
Hướng dẫn:
Áp dụng định lí cosin trong tam giác ABC tính BC: \(B{C^2} = A{B^2} + A{C^2} – 2AB.AC.\cos A\).
Cách giải:
Áp dụng định lí Cosin, ta có \(B{C^2} = A{B^2} + A{C^2} – 2AB.AC.\cos A\)
\( = {3^2} + {6^2} – 2.3.6.\cos {60^ \circ } = 27 \Leftrightarrow B{C^2} = 27 \Rightarrow B{C^2} + A{B^2} = A{C^2}.\)
Suy ra tam giác ABC vuông tại B do đó bán kính \(R = \frac{{AC}}{2} = 3\)
Chọn A.
Câu 8 (TH):
Cách giải:
Sau 2 giờ tàu B đi được 40 hải lí, tàu C đi được 30 hải lí. Vậy tam giác ABC có và
Áp dụng định lí côsin vào tam giác ABC ta có:
\({a^2} = {b^2} + {c^2} – 2bc.\cos A = {30^2} + {40^2} – 2.30.40.\cos {60^ \circ } = 900 + 1600 – 1200 = 1300\)
Vậy \(BC = \sqrt {1300} \approx 36\)(hải lí).
Sau 2 giờ, hai tàu cách nhau khoảng 36 hải lí.
Chọn B.
Câu 9 (TH):
Hướng dẫn:
Sử dụng \({\sin ^2}x + {\cos ^2}x = 1,{\mkern 1mu} {\mkern 1mu} \tan x = \frac{{\sin x}}{{\cos x}}\).
Cách giải:
Hai góc \(15^o\) và \(75^o\) phụ nhau nên \(\sin 75^o =\cos 15^o\)
Hai góc \(20^o\) và \(110^o\) hơn kém nhau \(90^o\) nên \(\sin 20^o =-\cos 110^o\)
Do đó,
\(\begin{array}{l}S = {\sin ^2}{15^ \circ } + {\cos ^2}{20^ \circ } + {\sin ^2}{75^ \circ } + {\cos ^2}{110^ \circ }\\ = {\sin ^2}{15^ \circ } + {\cos ^2}{20^ \circ } + {\cos ^2}{15^ \circ } + {\left( { – \sin {{20}^ \circ }} \right)^2}\\ = {\sin ^2}{15^ \circ } + {\cos ^2}{15^ \circ } + {\cos ^2}{20^ \circ } + \sin {20^ \circ }^2\\ = 2\end{array}\)
Chọn C.
Câu 10 (VD):
Hướng dẫn:
Sử dụng quy tắc ba điểm, phép nhân vectơ với một số.
Cách giải:
Từ giả thiết suy ra \(AC = a\sqrt 2 \)
Ta có \(P = \overrightarrow {AC} .\left( {\overrightarrow {CD} + \overrightarrow {CA} } \right) = \overrightarrow {AC} .\overrightarrow {CD} + \overrightarrow {AC} .\overrightarrow {CA} = – \overrightarrow {CA} .\overrightarrow {CD} – {\overrightarrow {AC} ^2}\)
\( = – CA.CD.\cos \left( {\overrightarrow {CA} ,\overrightarrow {CD} } \right) – A{C^2} = – a\sqrt 2 .a.\cos {45^ \circ } – {\left( {a\sqrt 2 } \right)^2} = – 3{a^2}\)
Chọn C.
Câu 11 (TH):
Hướng dẫn:
- \(\sqrt {P(x)} \) có nghĩa khi \(P(x) \ge 0\).
- \(\frac{{Q(x)}}{{\sqrt {P(x)} }}\) có nghĩa khi \(P(x) > 0\).
Cách giải:
Hàm số \(y = \sqrt {6 – 2x} – \frac{1}{{\sqrt {x + 1} }}\) xác định khi \(\left\{ \begin{array}{l}6 – 2x \ge 0\\x + 1 > 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x \le 3\\x > – 1\end{array} \right. \Leftrightarrow – 1 < x \le 3\)
Vậy tập xác định \(D = ( – 1;3]\)
Chọn C.
Câu 12 (TH):
Hướng dẫn:
Thay tọa độ các điểm vào hàm số
Cách giải:
Với \(x = – 5,x = 0\)thì \(y = \frac{{\sqrt {x – 3} + 10}}{{x + 5}}\) không xác định. Suy ra điểm \(( – 5;2)\) và \((0;6)\)không thuộc đồ thị hàm số
Với \(x = 4\) thì \(y = \frac{{\sqrt {4 – 3} + 10}}{{4 + 5}} = \frac{{11}}{9} \ne 1,1\). Suy ra điểm \((4;1,1)\)không thuộc đồ thị hàm số.
Với \(x = 7\) thì \(y = \frac{{\sqrt {7 – 3} + 10}}{{7 + 5}} = 1\). Suy ra điểm \((7;1)\) thuộc đồ thị hàm số.
Chọn A.
Câu 13 (TH):
Hướng dẫn:
Áp dụng phương pháp phân tích một vecto theo hai vecto cùng phương.
Tính chất trọng tâm của tam giác.
Cách giải:
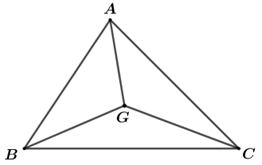
Vì \(G\) là trọng tâm của \(\Delta ABC\) nên \(\overrightarrow {GA} {\rm{\;}} + \overrightarrow {GB} {\rm{\;}} + \overrightarrow {GC} {\rm{\;}} = \vec 0\)\( \Rightarrow \overrightarrow {GC} {\rm{\;}} = {\rm{\;}} – \overrightarrow {GA} {\rm{\;}} – \overrightarrow {GB} \) .
Ta có: \(\overrightarrow {BC} {\rm{\;}} = \overrightarrow {BG} {\rm{\;}} + \overrightarrow {GC} \)\( \Rightarrow \overrightarrow {BC} {\rm{\;}} = {\rm{\;}} – \overrightarrow {GB} {\rm{\;}} + \overrightarrow {GC} \)
\( \Rightarrow \overrightarrow {BC} {\rm{\;}} = {\rm{\;}} – \overrightarrow {GA} {\rm{\;}} – 2\overrightarrow {GB} {\rm{\;}} = {\rm{\;}} – \vec a – 2\vec b\)\( = {\rm{\;}} – \overrightarrow {GB} {\rm{\;}} – \overrightarrow {GA} {\rm{\;}} – \overrightarrow {GB} \) \( = {\rm{\;}} – \overrightarrow {GA} {\rm{\;}} – 2\overrightarrow {GB} \)
Mà \(\overrightarrow {BC} {\rm{\;}} = m\vec a + n\vec b\) suy ra \(m = {\rm{\;}} – 1,{\mkern 1mu} {\mkern 1mu} n = {\rm{\;}} – 2\).
Chọn B.
Câu 14 (TH):
Cách giải:
Ta có \(\widehat {ABC} = {180^ \circ } – \left( {\widehat {BAC} + \widehat {ACB}} \right) = {75^ \circ } = \widehat {ACB}\)
Suy ra tam giác ABC cân tại A nên AB=AC=4.
Diện tích tam giác ABC là \({S_{\Delta ABC}} = \frac{1}{2}AB.AC.\sin \widehat {BAC} = 4\)
Chọn C.
Câu 15 (NB):
Cách giải:
Với \(a > 0\), ta có bảng biến thiên
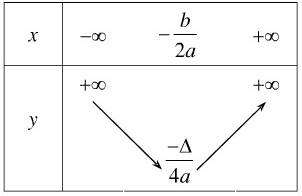
Hàm số đồng biến trên \(\left( { – \frac{b}{{2a}}; + \infty } \right).\)
Chọn B.
Câu 16 (TH):
Hướng dẫn:
Đối với bảng phân bố tần số, phương sai được tính theo công thức:
\({s^2} = \frac{1}{N}\left[ {{n_1}{{\left( {{x_1} – \bar x} \right)}^2} + {n_2}{{\left( {{x_2} – \bar x} \right)}^2} + {\rm{\;}} \ldots {\rm{\;}} + {n_k}{{\left( {{x_k} – \bar x} \right)}^2}} \right]\)
Với \({n_i};{\mkern 1mu} {\mkern 1mu} {f_i}\) lần lượt là tần số, tần suất của giá trị \({x_i}\).
Cách giải:
Bảng phân số tần số:

*) Sản lượng trung bình của 40 thửa ruộng là:
\(\bar x = \frac{{20.5 + 21.8 + 22.11 + 23.10 + 24.6}}{{40}} = 22,1{\mkern 1mu} \)(tạ)
*) Phương sai:
\({s^2} = \frac{1}{{40}}\left[ {5.{{\left( {20 – 22,1} \right)}^2} + 8.{{\left( {21 – 22,1} \right)}^2} + 11.{{\left( {22 – 22,1} \right)}^2} + 10.{{\left( {23 – 22,1} \right)}^2} + 6.{{\left( {24 – 22,1} \right)}^2}} \right]\)\( = 1,54\) (tạ)
*) Độ lệch chuẩn
\(s = \sqrt {1,54} \approx 1,24\)
Chọn A.
Câu 17 (NB):
Hướng dẫn:
Liệt kê các ước chung của 36 và 120.
Cách giải:
Ta có \(\left\{ \begin{array}{l}36 = {2^2}{.3^2}\\120 = {2^3}.3.5\end{array} \right.\). Do đó \(A = \left\{ {1;2;3;4;6;12} \right\}\).
Chọn A.
Câu 18 (NB):
Hướng dẫn:
\(A \cap B = \{ x \in A\) và \(x \in B\} .\)
\(A \cup B = \{ x \in A\) hoặc \(x \in B\} .\)
\(A\backslash B = \{ x \in A\) và \(x \notin B\} .\)
Cách giải:
Ta có: \(A = \left\{ {0;1;2;3;4} \right\},{\rm{ }}B = \left\{ {1;3;4;6;8} \right\}.\)
\(A \cap B = \{ 1;3;4\} \ne B.\)
\(A \cup B = \{ 0;1;2;3;4;6;8\} \ne A.\)
\(A\backslash B = \left\{ {0;2} \right\}.\)
\(B\backslash A = \{ 6;8\} \ne \left\{ {0;4} \right\}.\)
Chọn C.
Câu 19 (NB):
Hướng dẫn:
Thay tọa độ điểm M vào từng hệ bất phương trình.
Cách giải:
Thay tọa độ \(M\left( {0; – 3} \right)\) vào biểu thức \(2x – y\)ta được: \(2.0 – ( – 3) = 3\) \( \Rightarrow \)Loại B, D.
Thay tọa độ \(M\left( {0; – 3} \right)\) vào biểu thức \(3x + 5y\)ta được: \(3.0 + 5.( – 3) = – 15\) \( \Rightarrow \)Loại C
Chọn A.
Câu 20 (TH):
Hướng dẫn:
Bước 1. Biểu diễn miền nghiệm của hệ BPT
Bước 2. Xác định tọa độ đỉnh của miền nghiệm
Bước 3. Tính giá trị của F tại các đỉnh. KL giá trị nhỏ nhất.
Cách giải:
Ta có \(\left\{ {\begin{array}{*{20}{c}}{y – 2x \le 2}\\{2y – x \ge 4}\\{x + y \le 5}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{y – 2x – 2 \le 0}\\{2y – x – 4 \ge 0}\\{x + y – 5 \le 0}\end{array}} \right..\) \(\left( * \right)\)
Trong mặt phẳng tọa độ \(Oxy,\)vẽ các đường thẳng
\(\begin{array}{l}{d_1}:y – 2x – 2 = 0,\,\,{\rm{ }}{d_2}:2y – x – 4 = 0,{\rm{ }}\\{\rm{ }}{d_3}:x + y – 5 = 0.\end{array}\)
Khi đó miền nghiệm của hệ bất phương trình \(\left( * \right)\) là phần mặt phẳng (tam giác \(ABC\) kể cả biên) tô màu như hình vẽ.
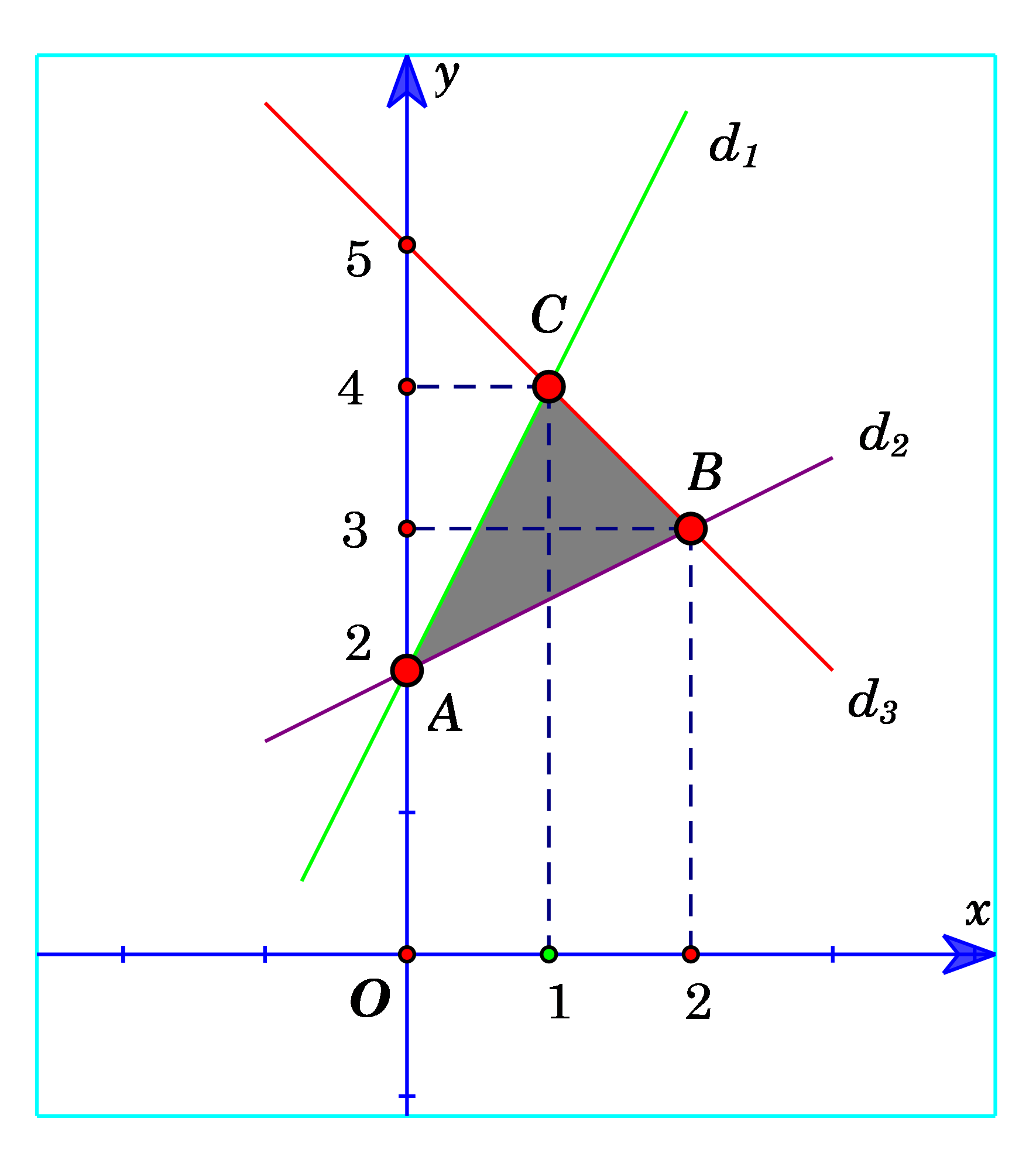
Xét các đỉnh của miền khép kín tạo bởi hệ \(\left( * \right)\) là
\(A\left( {0;2} \right),{\rm{ }}B\left( {2;3} \right),{\rm{ }}C\left( {1;4} \right).\)
Ta có \(\left\{ \begin{array}{l}F\left( {0;2} \right) = 2\\F\left( {2;3} \right) = 1\\F\left( {1;4} \right) = 3\end{array} \right. \Rightarrow {\rm{ }}{F_{\min }} = 1{\rm{ }}{\rm{.}}\)
Chọn A.
Câu 21 (TH):
Cách giải:
Hàm số bậc hai cần tìm có phương trình: \(y = a{x^2} + bx + c\left( {a \ne 0} \right)\)
Đồ thị là parabol có hoành độ đỉnh là \(\frac{5}{2}\)và đi qua \(A\left( {1; – 4} \right)\)
\( \Rightarrow \left\{ \begin{array}{l}\frac{{ – b}}{{2a}} = \frac{5}{2}\\a + b + c = – 4\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}\frac{{ – b}}{a} = 5\\a + b + c = – 4\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}b = – 5a\\a + b + c = – 4\end{array} \right.\)
\(A\left( {1; – 4} \right)\) không thuộc hàm số \(y = {x^2} – 5x + 8\)=> Loại A.
Hàm số \(y = 2{x^2} + 10x – 16\) có \(b = 10,a = 2 \Rightarrow b \ne – 5a\) => Loại B
Hàm số \(y = {x^2} – 5x\) có \(b = – 5,a = 1 \Rightarrow b = – 5a\), đi qua \(A\left( {1; – 4} \right)\) (TM)
Hàm số \(y = – 2{x^2} + 5x + 1\) có \(b = 5,a = – 2 \Rightarrow b \ne – 5a\) => Loại D
Chọn C.
Câu 22 (VD):
Hướng dẫn:
Chia cả tử và mẫu biểu thức P cho \(\cos \alpha \) và biểu diễn biểu thức P theo \(\tan \alpha \).
Cách giải:
Ta có \(P = \frac{{6\sin \alpha – 7\cos \alpha }}{{6\cos \alpha + 7\sin \alpha }} = \frac{{6\frac{{\sin \alpha }}{{\cos \alpha }} – 7}}{{6 + 7\frac{{\sin \alpha }}{{\cos \alpha }}}} = \frac{{6\tan \alpha – 7}}{{6 + 7\tan \alpha }} = \frac{5}{3}\)
Chọn B.
Câu 23 (TH):
Hướng dẫn:
Áp dụng định nghĩa tích của vecto với một số, quy tắc cộng vecto để phân tích vecto.
Cách giải:
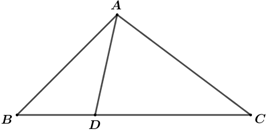
Ta có:
\(\overrightarrow {AD} {\rm{\;}} = \overrightarrow {AB} {\rm{\;}} + \overrightarrow {BD} {\rm{\;}} = \overrightarrow {AB} {\rm{\;}} + \frac{1}{3}\overrightarrow {BC} \)
\({\mkern 1mu} = \overrightarrow {AB} {\rm{\;}} + \frac{1}{3}\left( {\overrightarrow {BA} {\rm{\;}} + \overrightarrow {AC} } \right)\)\( = \overrightarrow {AB} {\rm{\;}} – \frac{1}{3}\overrightarrow {AB} {\rm{\;}} + \frac{1}{3}\overrightarrow {AC} \)\({\mkern 1mu} {\mkern 1mu} = \frac{2}{3}\overrightarrow {AB} {\rm{\;}} + \frac{1}{3}\overrightarrow {AC} \)
\( \Rightarrow \overrightarrow {AD} {\rm{\;}} = \frac{2}{3}\overrightarrow {AB} {\rm{\;}} + \frac{1}{3}\overrightarrow {AC} \)
Chọn A.
Câu 24 (NB):
Hướng dẫn:
Áp dụng các tính chất của phép nhân véctơ với một số.
Cách giải:
Với \(\vec a,{\mkern 1mu} {\mkern 1mu} \vec b\) tùy ý; \(\forall k,{\mkern 1mu} {\mkern 1mu} h \in \mathbb{R}\) ta có:
+) \(0.\vec a = 0\) là đáp án sai vì \(0.\vec a = \vec 0\).
+) \(k\left( {\vec a + \vec b} \right) = k\vec a + k\vec b\) (đúng)
+) \(k.\vec 0 = \vec 0\) (đúng)
+) \(h\left( {k\vec a} \right) = \left( {hk} \right)\vec a\) (đúng)
Chọn A.
Câu 25 (NB):
Cách giải:
Dùng Pitago tính được \(AC = 8\), suy ra \(p = \frac{{AB + BC + CA}}{2} = 12\)
Diện tích tam giác vuông \(S = \frac{1}{2}AB.AC = 24\) .Lại có \(S = p.r \Rightarrow r = \frac{S}{p}2cm\)
Chọn C.
Câu 26 (TH):
Cách giải:
Chu vi của miếng đất là
\(P = 2\left[ {x + y} \right] = 2.\left[ {\left( {43 \pm 0,5} \right) + \left( {63 \pm 0,5} \right)} \right]\)
\( = 2.\left[ {\left( {43 + 63} \right) \pm \left( {0,5 + 0,5} \right)} \right] = 212 \pm 2.\)
Chọn B.
Câu 27 (TH):
Hướng dẫn:
Khoảng biến thiên, kí hiệu là R, là hiệu số giữa giá trị lớn nhất và giá trị nhỏ nhất.
Cách giải:
Giá trị lớn nhất là 20
Giá trị nhỏ nhất là 1
Vậy khoảng biến thiên của mẫu số liệu là: \(R = 20 – 1 = 19\)
Chọn C.
Câu 28 (TH):
Cách giải:
Đồ thị hàm số cắt trục tung tại điểm \(\left( {0\,\,;\,\, – 1} \right)\) nên \(c = – 1\).
Tọa độ đỉnh \(I\left( {1\,\,;\, – 2} \right)\), ta có phương trình: \(\left\{ \begin{array}{l} – \frac{b}{{2a}} = 1\\a{.1^2} + b.1 – 1 = – 2\end{array} \right.\) \( \Leftrightarrow \left\{ \begin{array}{l}2a + b = 0\\a + b = – 1\end{array} \right.\) \( \Leftrightarrow \left\{ \begin{array}{l}a = 1\\b = – 2\end{array} \right.\).
Vậy parabol cần tìm là: \(y = {x^2} – 2x – 1\).
Chọn C.
Câu 29 (TH):
Cách giải:
Hàm số \(y = – {x^2} + 4x – 5\) có \(a = – 1 < 0\), nên loại C,D.
Hoành độ đỉnh \({x_I} = – \frac{b}{{2a}} = – \frac{4}{{2.( – 1)}} = 2\)
Chọn B.
Câu 30 (NB):
Hướng dẫn:
Sử dụng định nghĩa tích vô hướng của hai vectơ:\(\overrightarrow a .\overrightarrow b = \left| {\overrightarrow a } \right|.\left| {\overrightarrow b } \right|.\cos \left( {\overrightarrow a ,\overrightarrow b } \right)\)
Cách giải:
Xác định được góc \(\left( {\overrightarrow {AB} ,\overrightarrow {BC} } \right)\) là góc ngoài của góc \(\widehat B\) nên \(\left( {\overrightarrow {AB} ,\overrightarrow {BC} } \right) = {120^ \circ }\)
Do đó \(\overrightarrow {AB} .\overrightarrow {BC} = AB.BC.\cos \left( {\overrightarrow {AB} ,\overrightarrow {BC} } \right) = a.a.\cos {120^ \circ } = – \frac{{{a^2}}}{2}\)
Chọn C.
Phần 2: Tự luận (4 điểm)
Câu 1 (VD):
Hướng dẫn:
a)
* Số trung bình của mẫu số liệu \({x_1},{\mkern 1mu} {\mkern 1mu} {x_2},{\mkern 1mu} {\mkern 1mu} ….,{\mkern 1mu} {\mkern 1mu} {x_n}\) kí hiệu là \(\bar x\), được tính bằng công thức:
\(\bar x = \frac{{{m_1}{x_2} + {m_2}{x_2} + … + {m_k}{x_k}}}{n}\)
Trong đó mk là tần số của giá trị xk và \(n = {m_1} + {m_2} + … + {m_k}\).
Cách giải:
a) Mẫu số liệu thống kê nhiệt độ nhận được từ bảng là:
23 25 26 27 27 27 27 21 19 18
b)
* Nhiệt độ trung bình của 10 ngày liên tiếp ở Nghệ An cuối tháng 01 năm 2022 là:
\(\bar x = \frac{{23 + 25 + 26 + 27 + 27 + 27 + 27 + 21 + 19 + 18}}{{10}} = 24\) (\(^oC\))
* Phương sai
\({s^2} = \frac{1}{{10}}({23^2} + {25^2} + {26^2} + {4.27^2} + {21^2} + {19^2} + {18^2}) – {24^2} = 11,2\)
* Độ lệch chuẩn
\(s = \sqrt {11,2} \approx 3,35\)
Câu 2 (VD):
Cách giải:
a) Gọi I là trung điểm \({\rm{BC}}\) ta có:
\(|\overrightarrow {{\rm{MB}}} + \overrightarrow {{\rm{MC}}} | = |\overrightarrow {{\rm{MB}}} – \overrightarrow {{\rm{MC}}} | \Leftrightarrow {\rm{ }}|\overrightarrow {{\rm{MI}}} | = |\overrightarrow {{\rm{CB}}} | \Leftrightarrow {\rm{MI}} = \frac{{{\rm{BC}}}}{2}\)
Vậy tập hợp điểm \({\rm{M}}\) là đường tròn tâm \({\rm{I}}\), bán kính \({\rm{R}} = \frac{{{\rm{BC}}}}{2}\).
b) Gọi \({\rm{K}}\) là điểm thoả mān:
L là điểm thoả mān: \(3\overrightarrow {{\rm{LB}}} + 2\overrightarrow {{\rm{LC}}} = \vec 0\)
Ta có: \(|2\overrightarrow {{\rm{MA}}} + 3\overrightarrow {{\rm{MB}}} | = |3\overrightarrow {{\rm{MB}}} + 2\overrightarrow {{\rm{MC}}} |\)
\( \Leftrightarrow |5\overrightarrow {{\rm{MK}}} | = |5\overrightarrow {{\rm{ML}}} | \Leftrightarrow {\rm{MK}} = {\rm{ML}}\)
\( \Rightarrow \) Tập hợp điểm \({\rm{M}}\) là đường trung trực của đoạn thẳng \({\rm{KL}}\).
c) Với I là trung điểm của \({\rm{BC}}\). Gọi \({\rm{J}}\) là điểm thoả mān: \(4\overrightarrow {{\rm{JA}}} + \overrightarrow {{\rm{JB}}} + \overrightarrow {{\rm{JC}}} = \vec 0\)
Ta có:
\(|4\overrightarrow {{\rm{MA}}} + \overrightarrow {{\rm{MB}}} + \overrightarrow {{\rm{MC}}} | = |2\overrightarrow {{\rm{MA}}} – \overrightarrow {{\rm{MB}}} – \overrightarrow {{\rm{MC}}} |\)
\( \Leftrightarrow |6\overrightarrow {{\rm{MJ}}} | = |2\overrightarrow {{\rm{MA}}} – 2\overrightarrow {{\rm{MI}}} | \Leftrightarrow |6\overrightarrow {{\rm{MJ}}} | = |2\overrightarrow {{\rm{IA}}} | \Leftrightarrow {\rm{MJ}} = \frac{1}{3}{\rm{IA}} = \) const
Vậy tập hợp điểm \(M\) là đường tròn tâm \({\rm{J}}\) bán kính \({\rm{R}} = \frac{1}{3}{\rm{IA}}\).
Câu 3 (VD):
Cách giải:
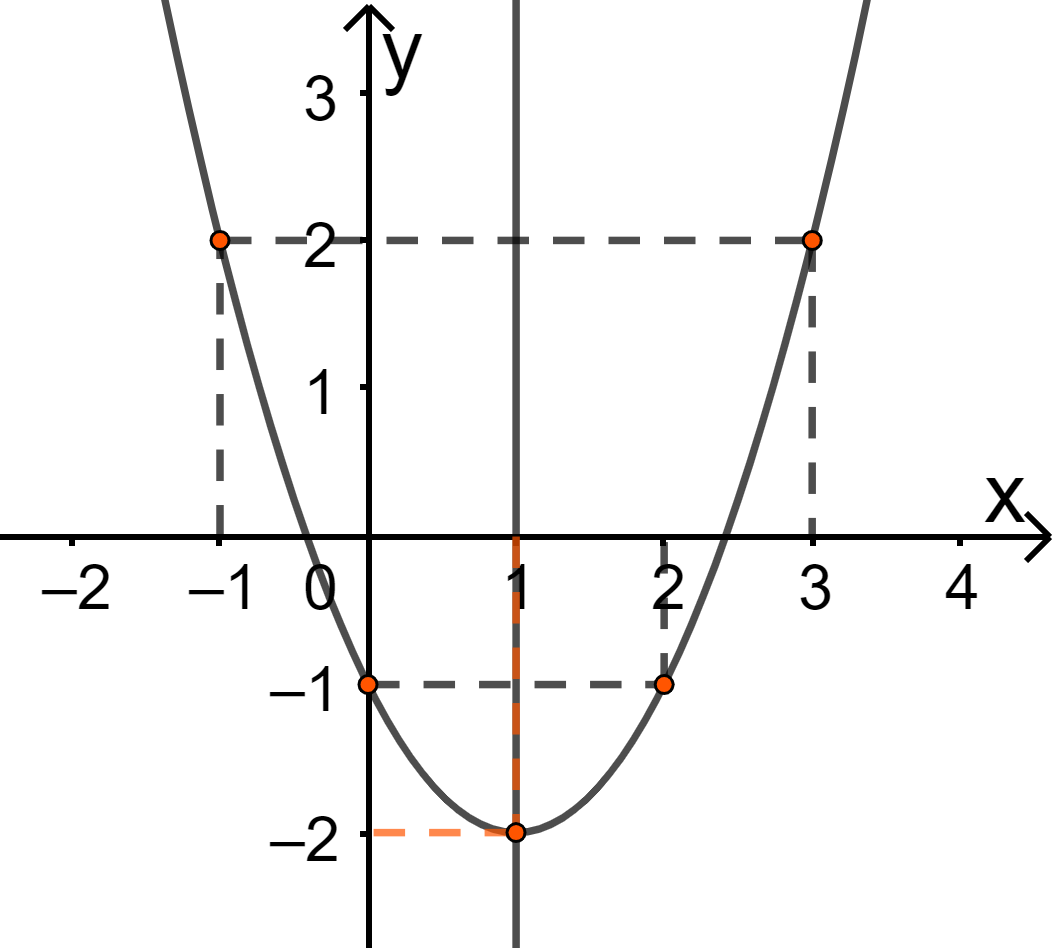
Parabol (P) \(y = a{x^2} + bx + c\) giao với Oy tại điểm có tọa độ \((0;c)\), do đó \(c = – 1\)
(P) có hoành độ đỉnh \({x_I} = – \frac{b}{{2a}} = 1 \Rightarrow b = – 2a\)
Điểm \(I(1; – 2)\) thuộc (P) nên \(a{.1^2} + b.1 – 1 = – 2\) hay \(a + b = – 1\)
Từ đó ta có hệ phương trình \(\left\{ \begin{array}{l}a + b = – 1\\b = – 2a\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}b = – 2\\a = 1\end{array} \right.\)
Vậy parabol cần tìm là \(y = {x^2} – 2x – 1\)
* Vẽ parabol
Đỉnh \(I(1; – 2)\)
Trục đối xứng \(x = 1\)
Giao với Oy tại A(0;-1), lấy điểm B(2;-1) đối xứng với A qua trục đối xứng
Lấy điểm C(-1;2) và D(3;2) thuộc đồ thị.