Lời giải Giải đề 3 Tổng hợp 10 đề thi học kì 1 Toán 10 Chân trời sáng tạo – Đề thi đề kiểm tra Toán lớp 10 Chân trời sáng tạo.
Câu hỏi/Đề bài:
HƯỚNG DẪN GIẢI CHI TIẾT
Phần I: Trắc nghiệm (6 điểm)
|
1.B |
2.A |
3.A |
4.D |
5.B |
6.C |
7.A |
8.C |
9.D |
10.A |
|
11.C |
12.A |
13.D |
14.C |
15.C |
16.C |
17.C |
18.B |
19.A |
20.D |
|
21.C |
22.B |
23.C |
24.C |
25.C |
26.B |
27.B |
28.A |
29.D |
30.D |
Câu 1 (NB):
Hướng dẫn:
Mệnh đề có tính đúng hoặc sai.
Cách giải:
b, c là mệnh đề
Chọn B.
Câu 2 (NB):
Hướng dẫn:
Tìm giá trị để mệnh đề đúng hoặc sai để khẳng định.
Cách giải:
A: Đúng vì \({x^2} \ge 0\) nên \({x^2} + 1 > 0\).
Chọn A.
Câu 3 (TH):
Hướng dẫn:
Dùng định nghĩa các phép toán trên tập hợp.
Cách giải:
A. Đúng vì \(\left\{ {a;c} \right\}\) vừa thuộc tập A, vừa thuộc tập B.
B. HS nhầm là vừa thuộc A hoặc B.
C. HS nhầm là thuộc A và không thuộc B.
D. HS nhầm là thuộc B và không thuộc A.
Chọn A.
Câu 4 (NB):
Hướng dẫn:
Cách giải:
Theo biểu đồ Ven thì phần gạch sọc trong hình vẽ là tập hợp \(A \cap B\).
Chọn D.
Câu 5 (TH):
Hướng dẫn:
Tính số học sinh chỉ xếp loại giỏi, chỉ xếp hạnh kiểm tốt. Từ đó tính số học sinh có học lực giỏi hoặc hạnh kiểm tốt.
Cách giải:
Từ giả thiết bài toán, ta có:
Số các học sinh chỉ có học lực giỏi là: \(15 – 10 = 5\).
Số các học sinh chỉ được xếp loại hạnh kiểm tốt là: \(25 – 10 = 15\).
Tổng số học sinh có học lực giỏi hoặc hạnh kiểm tốt là \(10 + 5 + 15 = 30\).
Vậy có \(30\) học sinh được khen thưởng.
Chọn B.
Câu 6 (VD):
Hướng dẫn:
Dùng định nghĩa phép toán trên tập hợp hoặc vẽ tia số.
Cách giải:
Ta có: \(\left( {A \cup B} \right) = \mathbb{R}\)\( \Leftrightarrow – 1 \le m + 1 \Leftrightarrow m \ge – 2\).
Chọn C.
Câu 7 (NB):
Hướng dẫn:
Thay tọa độ x, y vào bât phương trình và kiểm tra tính đúng sai
Cách giải:
Vì 2.0+3.0 = 0
Chọn D.
Câu 7 (TH):
Hướng dẫn:
Lấy điểm bất kì thuộc hoặc không thuộc miền nghiệm để kiểm tra bất phương trình trong đáp án
Cách giải:
Ta thấy O(0,0) không thuộc miền nghiệm nên loại B,C
Đường thẳng qua (1,0) nên đáp án A đúng
Chọn A.
Câu 8 (TH):
Hướng dẫn:
Rút gọn bất phương trình và thay tọa độ các điểm vào bất phương trình để kiểm tra tính đúng sai.
Cách giải:
\(\begin{array}{l}3x + 2\left( {y + 3} \right) > 4\left( {x + 1} \right) – y + 3\\ \Leftrightarrow 3x + 2y + 6 > 4x + 4 – y + 3\\ \Leftrightarrow – x + 3y > 1\end{array}\)
Vì thay x = 2, y = 1 vào bất phương trình ta thấy – 2 + 3.1 =1 nên (2,1) thuộc miền nghiệm
Chọn C.
Câu 9 (NB):
Hướng dẫn:
Cách giải:
Ra quyết định dựa trên số liệu không phụ thuộc vào công việc của môn Thống kê.
Chọn D.
Câu 10 (NB):
Hướng dẫn:
Mốt của dấu hiệu là giá trị có tần số lớn nhất.
Cách giải:
Vì 5 có tần suất là 2, còn 6,2,9,10,8 đều có tần suất là 1 nên mốt của dấu hiệu là 5.
Chọn A.
Câu 11 (TH):
Hướng dẫn:
Lập bảng tần số, sắp xếp các giá trị thống kê theo thứ tự không giảm.
Nếu có n (n lẻ) n = 2k+1 giá trị thì số trung vị bằng giá trị thứ k
Nếu có n (chẵn) n= 2k giá trị thì số trung vị bằng trung bình cộng 2 giá trị k-1 và k+1.
Cách giải:
|
32 |
33 |
36 |
38 |
39 |
42 |
48 |
|
1 |
2 |
1 |
1 |
1 |
1 |
2 |
Vì có 7 giá trị nên trung vị bằng số liệu thứ 4 là 38
Chọn C.
Câu 12 (TH):
Hướng dẫn:
Số trung bình là \(\overline x = \frac{{{x_1} + {x_2} + {x_3} + … + {x_n}}}{n}\)
Cách giải:
\(\overline x = \frac{{{x_1} + {x_2} + {x_3} + … + {x_n}}}{n} = \frac{{8 + 10 + 12 + 14 + 16}}{5} = 12\)
Chọn A.
Câu 13 (TH):
Hướng dẫn:
Kích thước mẫu là số các số liệu thống kê.
Cách giải:
Kích thước mẫu bằng 1120+1075+900 = 3095
Chọn D.
Câu 14 (NB):
Hướng dẫn:
Độ lệch chuẩn là căn bậc hai của phương sai.
Cách giải:
Độ lệch chuẩn là căn bậc hai của phương sai.
Chọn C.
Câu 15 (TH):
Hướng dẫn:
Chú ý không rút gọn biểu thức trước khi tìm tập xác định.
Cách giải:
Hàm số xác định khi \(\left\{ \begin{array}{l}x + 1 \ne 0\\{x^2} + 3x + 4 \ne 0\end{array} \right. \Leftrightarrow x \ne – 1.\)
Vậy tập xác định của hàm số là \({\rm{D}} = \mathbb{R}\backslash \left\{ { – 1} \right\}.\)
Chọn C.
Câu 16 (TH):
Hướng dẫn:
Thay tọa độ từng điểm và kiểm tra.
Cách giải:
Xét đáp án A, thay \(x = 2\) và \(y = 0\) vào hàm số ta được\(0 = \frac{{\sqrt {{2^2} – 4.2 + 4} }}{2}\): thỏa mãn.
Xét đáp án B, thay \(x = 3\) và \(y = \frac{1}{3}\) vào hàm số ta được \(\frac{1}{3} = \frac{{\sqrt {{3^2} – 4.3 + 4} }}{3}\): thỏa mãn.
Xét đáp án C, thay \(x = 1\) và \(y = – 1\) vào hàm số ta được \( – 1 = \frac{{\sqrt {{1^2} – 4.1 + 4} }}{1} \Leftrightarrow – 1 = 1\)không thỏa mãn.
Chọn C.
Câu 17 (TH):
Hướng dẫn:
Kiểm tra các giá trị cần tính thuộc điều kiện nào của hàm số trước khi tính.
Cách giải:
Khi \(x \ge 2\) thì \(f\left( 2 \right) = \frac{{2\sqrt {2 + 2} – 3}}{{2 – 1}} = 1.\)
Khi \(x < 2\) thì .\(f\left( { – 2} \right) = {\left( { – 2} \right)^2} + 1 = 5.\). Vậy \(f\left( 2 \right) + f\left( { – 2} \right) = 6.\)
Chọn C.
Câu 18 (TH):
Hướng dẫn:
Tìm đỉnh dồ thị hàm số và vẽ bảng biến thiên.
Cách giải:
Đỉnh S (2, 1), bề lõm quay lên nên hàm số đồng biến trên \(\left( { – \infty ;2} \right)\)và nghịch biến trên \(\left( {2; + \infty } \right)\).
Chọn B.
Câu 19 (TH):
Hướng dẫn:
Trục đối xứng của hàm số bậc hai là \(x = \frac{{ – b}}{{2a}}\)
Cách giải:
Trục đối xứng của hàm số bậc hai là \(x = \frac{{ – b}}{{2a}} = \frac{{ – 1}}{{2.1}} = \frac{{ – 1}}{2}\)
Chọn A.
Câu 20 (VDC):
Hướng dẫn:
Tìm tập xác định của hàm số theo m
Cho tập hợp tìm được là tập con của \(\left( {0; + \infty } \right).\)
Cách giải:
Hàm số xác định khi \(\left\{ \begin{array}{l}x – m \ge 0\\2x – m – 1 \ge 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x \ge m\\x \ge \frac{{m + 1}}{2}\end{array} \right. & \left( * \right)\).
Ÿ TH1: Nếu \(m \ge \frac{{m + 1}}{2} \Leftrightarrow m \ge 1\) thì \(\left( * \right) \Leftrightarrow x \ge m\). Suy ra tập xác định của hàm số là \({\rm{D}} = \left[ {m; + \infty } \right)\)
Khi đó, hàm số xác định trên \(\left( {0; + \infty } \right)\) khi và chỉ khi \(\left( {0; + \infty } \right) \subset \left[ {m; + \infty } \right) \Leftrightarrow m \le 0\).Không thỏa mãn điều kiện \(m \ge 1\).
Ÿ TH2: Nếu \(m \le \frac{{m + 1}}{2} \Leftrightarrow m \le 1\) thì \(\left( * \right) \Leftrightarrow x \ge \frac{{m + 1}}{2}\). Suy ra tập xác định của hàm số là \({\rm{D}} = \left[ {\frac{{m + 1}}{2}; + \infty } \right)\).
Khi đó, hàm số xác định trên \(\left( {0; + \infty } \right)\) khi và chỉ khi \(\left( {0; + \infty } \right) \subset \left[ {\frac{{m + 1}}{2}; + \infty } \right)\) \( \Leftrightarrow \frac{{m + 1}}{2} \le 0 \Leftrightarrow m \le – 1\) (Thỏa mãn điều kiện \(m \le 1\)). Vậy \(m \le – 1\) thỏa yêu cầu bài toán.
Chọn D.
Câu 21 (NB):
Hướng dẫn:
Áp dụng định lý cosin \(\cos A = \frac{{{b^2} + {c^2} – {a^2}}}{{2bc}}\)
Cách giải:
\(\cos A = \frac{{{b^2} + {c^2} – {a^2}}}{{2bc}} = \frac{{{8^2} + {5^2} – {7^2}}}{{2.8.5}} = \frac{1}{2} \Rightarrow \angle A = {60^0}\)
Chọn C.
Câu 22 (TH):
Hướng dẫn:
Áp dụng định lý cosin \(\cos C = \frac{{{b^2} + {a^2} – {c^2}}}{{2ab}}\)
Cách giải:
Theo định lí hàm cosin, ta có
\(A{B^2} = A{C^2} + B{C^2} – 2.AC.BC.\cos \widehat C \Rightarrow {\left( {\sqrt 2 } \right)^2} = {\left( {\sqrt 3 } \right)^2} + B{C^2} – 2.\sqrt 3 .BC.\cos 45^\circ \)\( \Rightarrow BC = \frac{{\sqrt 6 + \sqrt 2 }}{2}\)
Chọn B.
Câu 23 (TH):
Hướng dẫn:
Áp dụng công thức Herong.
Cách giải:
Đặt \(p = \frac{{AB + BC + CA}}{2} = 24.\) Áp dụng công thức Hê – rông, ta có
\({S_{\Delta ABC}} = \sqrt {p\left( {p – AB} \right)\left( {p – BC} \right)\left( {p – CA} \right)} = \sqrt {24.\left( {24 – 21} \right).\left( {24 – 17} \right).\left( {24 – 10} \right)} = 84\,\,c{m^2}.\)
Vậy bán kính cần tìm là \({S_{\Delta ABC}} = \frac{{AB.BC.CA}}{{4R}} \Rightarrow R = \frac{{AB.BC.CA}}{{4.{S_{\Delta ABC}}}} = \frac{{21.17.10}}{{4.84}} = \frac{{85}}{8}\,\,cm.\)
Chọn C.
Câu 24 (TH):
Hướng dẫn:
Dùng công thức \(S = p.r\)
Cách giải:
Dùng Pitago tính được \(AC = 8\), suy ra \(p = \frac{{AB + BC + CA}}{2} = 12\).
Diện tích tam giác vuông \(S = \frac{1}{2}AB.AC = 24\).Lại có
Chọn C.
Câu 25 (NB):
Hướng dẫn:
I là trung điểm của AB thì IA = IB và \(\overrightarrow {IA} \), \(\overrightarrow {IB} \) ngược hướng
Cách giải:
IA = IB và \(\overrightarrow {IA} \), \(\overrightarrow {IB} \) ngược hướng nên \(\overrightarrow {IA} = – \overrightarrow {IB} .\)
Chọn C.
Câu 26 (TH):
Hướng dẫn:
Dùng định nghĩa hai vecto bằng nhau.
Cách giải:
Ta có \(\overrightarrow {AB} = – \overrightarrow {CD} = \overrightarrow {DC} \). Do đó:
Ÿ \(\overrightarrow {AB} \) và \(\overrightarrow {CD} \) ngược hướng.
Ÿ \(\overrightarrow {AB} \) và \(\overrightarrow {CD} \) cùng độ dài.
Ÿ \(ABCD\) là hình bình hành nếu \(\overrightarrow {AB} \) và \(\overrightarrow {CD} \) không cùng giá.
Ÿ \(\overrightarrow {AB} + \overrightarrow {CD} = \overrightarrow 0 .\)
Chọn B.
Câu 27 (NB):
Hướng dẫn:
Dùng quy tắc cộng hai veto và hai vecto bằng nhau.
Cách giải:
\(\overrightarrow {AO} – \overrightarrow {DO} = \overrightarrow {AO} + \overrightarrow {OD} = \overrightarrow {AD} = \overrightarrow {BC} \)
Chọn B.
Câu 28 (NB):
Hướng dẫn:
Tích vô hướng \(\overrightarrow a .\overrightarrow b = \left| {\overrightarrow a } \right|.\left| {\overrightarrow b } \right|.\cos (\overrightarrow a ,\overrightarrow b )\)
Cách giải:
Ta có \((\overrightarrow {AB} ,\overrightarrow {AC} ) = \widehat {BAC} = {45^0}\) nên \(\overrightarrow {AB} .\overrightarrow {AC} = AB.AC.\cos {45^0} = a.a.\sqrt 2 .\frac{{\sqrt 2 }}{2} = {a^2}\).
Chọn A.
Câu 29 (TH):
Hướng dẫn:
Tích vô hướng \(\overrightarrow a .\overrightarrow b = \left| {\overrightarrow a } \right|.\left| {\overrightarrow b } \right|.\cos (\overrightarrow a ,\overrightarrow b )\)
Cách giải:
Gọi giao điểm của AC và BD là O, giả thiết không cho góc, ta phân tích các vectơ theo các vectơ có giá vuông góc với nhau.
Ta có \(\overrightarrow {AB} .\overrightarrow {AC} = \left( {\overrightarrow {AO} + \overrightarrow {OB} } \right)\overrightarrow {AC} = \overrightarrow {AO} .\overrightarrow {AC} + \overrightarrow {OB} .\overrightarrow {AC} = \frac{1}{2}\overrightarrow {AC} .\overrightarrow {AC} + 0 = \frac{1}{2}A{C^2} = 32\).
Chọn D.
Câu 30 (VD):
Hướng dẫn:
Tích vô hướng \(\overrightarrow a .\overrightarrow b = \left| {\overrightarrow a } \right|.\left| {\overrightarrow b } \right|.\cos (\overrightarrow a ,\overrightarrow b )\)
Cách giải:
Ta có \({S_{ABCD}} = 2{S_{ABC}} = 54 \Leftrightarrow {S_{ABC}} = 27c{m^2}\). Diện tích tam giác ABC là:
\({S_{ABC}} = \frac{1}{2}.AB.BC.\sin \widehat {ABC} = \frac{1}{2}.AB.AD.\sin \widehat {ABC} \Rightarrow \sin \widehat {ABC} = \frac{{2{S_{ABC}}}}{{AB.AD}} = \frac{{2.27}}{{8.12}} = \frac{9}{{12}}\)
\( \Rightarrow \cos \widehat {ABC} = \sqrt {1 – {{\sin }^2}\widehat {ABC}} = \frac{{5\sqrt 7 }}{{16}}\)
Mặt khác góc giữa hai vecto \(\overrightarrow {AB} ,\overrightarrow {BC} \) là góc ngoài góc \(\widehat {ABC}\).
Suy ra \(\cos \left( {\overrightarrow {AB} ,\overrightarrow {BC} } \right) = \cos \left( {{{180}^0} – \widehat {ABC}} \right) = \cos \widehat {ABC} = \frac{{ – 5\sqrt 7 }}{{16}}\).
Chọn D.
Phần II: Tự luận (4 điểm)
Câu 1 (TH):
Hướng dẫn:
Dùng định nghĩa hoặc biểu diễn trên tia số.
Cách giải:
a. Biểu diễn trên trục số ta được:
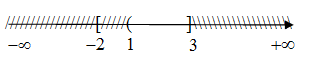
b. Ta có \(A = \left[ {1 – 2m;\,m + 3} \right]\), \(B = \left[ {8 – 5m;\, + \infty } \right)\).
\(A \cap B = \emptyset \) \( \Leftrightarrow \) \(\left\{ \begin{array}{l}m + 3 < 8 – 5m\\1 – 2m \le m + 3\end{array} \right.\) \( \Leftrightarrow \) \(\left\{ \begin{array}{l}6m < 5\\3m \ge – 2\end{array} \right.\) \( \Leftrightarrow \) \(\left\{ \begin{array}{l}m < \frac{5}{6}\\m \ge – \frac{2}{3}\end{array} \right.\) \( \Leftrightarrow \) \( – \frac{2}{3} \le m < \frac{5}{6}\).
Câu 2 (TH):
Hướng dẫn:
Xác định đỉnh, trục đối xứng, các điểm mà đồ thị đi qua
Cách giải:
a. Vì \(y = {x^2} – 2\left( {m + 1} \right)x + 3m – 3\) đi qua M (3, 0) nên thay x = 3, y = 0 ta có
0 = 9 – 2(m + 1).3 + 3m – 3. Suy ra 9 – 6m – 6 + 3m – 3 = 0. Suy ra m = 0.
Vậy hàm số là \(y = {x^2} – 2x – 3\)
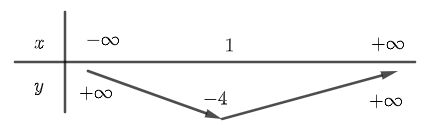
b. Đỉnh S của (P) có hoành độ \(x = \frac{{ – \left( { – 2} \right)}}{{2.1}} = 1\). Suy ra tung độ đỉnh S là y = 1 – 2 – 3 = – 4.
Vậy S (1, – 4), trục đối xứng x = 1
Bảng biến thiên:
Đồ thị:
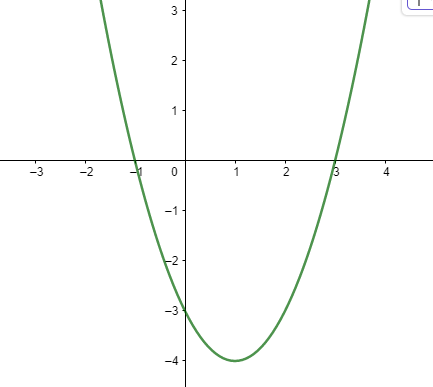
Đồ thị hàm số là 1 parabol có bề lõm quay lên, có đỉnh S (1,-4), trục đối xứng x = 1, cắt trục tung tại (0, -3), có giá trị nhỏ nhất bằng 0
Câu 3 (TH):
Hướng dẫn:
Dùng giá trị lượng giác trong tam giác vuông.
Cách giải:
Xét tam giác ABO vuông tại B. Khi đó \(AB = OB.\tan {60^0} = 60.\tan {60^0} = 60\sqrt 3 \)m
Ta có BD = OC =1 m.
Vậy chiều cao của tháp là AB + BD = \(60\sqrt 3 + 1 \approx 104,92\)m
Câu 4 (TH):
Hướng dẫn:
Tính chất trọng tâm tam giác, chứng minh \(MB \bot MG\).
Cách giải:
Gọi G là trọng tâm tam giác ABC. Suy ra \(\overrightarrow {MA} + \overrightarrow {MB} + \overrightarrow {MC} = 3\overrightarrow {MG} \)
Ta có \(\overrightarrow {MB} \left( {\overrightarrow {MA} + \overrightarrow {MB} + \overrightarrow {MC} } \right) = 0 \Rightarrow \overrightarrow {MB} .3\overrightarrow {MG} = 0 \Leftrightarrow \overrightarrow {MB} .\overrightarrow {MG} = 0 \Rightarrow MB \bot MG\)
Chứng tỏ \(MB \bot MG\) hay M nhìn đoạn BG dưới một góc vuông nên tập hợp các điểm M là đường tròn đường kính BG.