Phân tích và giải Đề kiểm tra học kì 2 Toán 10 – Đề số 5 – Chân trời sáng tạo – Đề thi học kì 2 – Đề thi đề kiểm tra Toán lớp 10 Chân trời sáng tạo. I. PHẦN TRẮC NGHIỆM ( 35 câu – 7,0 điểm )….
Đề thi:
I. TRẮC NGHIỆM (35 câu – 7,0 điểm)
Câu 1: Tìm \(m\) để hàm số \(y = \left( {2m + 1} \right)x + m – 3\) đồng biến trên \(\mathbb{R}.\)
A. \(m > \frac{1}{2}.\) B. \(m < \frac{1}{2}.\) C. \(m < – \frac{1}{2}.\) D. \(m > – \frac{1}{2}.\)
Câu 2: Tập xác định của hàm số \(y = \sqrt {x – 3} + \frac{1}{{x – 3}}\) là
A \(D = \mathbb{R}\backslash \left\{ 3 \right\}\).
B. \(D = \left[ {3; + \infty } \right)\).
C. \(D = \left( {3; + \infty } \right)\).
D. \(D = \left( { – \infty ;3} \right)\).
Câu 3: Parabol \(y = – 2{x^2} + 3x – 1\) có tọa độ đỉnh I là:
A. \(\left( {\frac{3}{4};\frac{1}{8}} \right).\)
B. \(\left( { – \frac{3}{2}; – 10} \right).\)
C. \(\left( {\frac{3}{2}; – 1} \right).\)
D. \(\left( {\frac{3}{4};\frac{{17}}{8}} \right).\)
Câu 4: Tìm parabol \(\left( P \right):y = a{x^2} + 3x – 2,\) biết rằng parabol có trục đối xứng \(x = – 3\)?
A. \(y = {x^2} + 3x – 2.\)
B. \(y = \frac{1}{2}{x^2} + x – 2.\)
C. \(y = \frac{1}{2}{x^2} + 3x – 3.\)
D. \(y = \frac{1}{2}{x^2} + 3x – 2.\)
Câu 5: Cho tam thức bậc hai \(f(x) = 5x – {x^2} – 6\). Tìm \(x\) để \(f(x) \ge 0\).
A. \(x \in \left( { – \infty ;2} \right] \cup \left[ {3; + \infty } \right)\).
B. \(x \in \left[ {2;3} \right]\).
C. \(x \in \left( { – \infty ;2} \right) \cup \left( {3; + \infty } \right)\).
D. \(x \in \left( {2;3} \right)\).
Câu 6: Cho tam thức bậc hai \(f\left( x \right) = {x^2} – 5x + 6\) và a là số thực lớn hơn 3. Tìm khẳng định đúng trong các khẳng định sau.
A. \(f\left( a \right) < 0.\)
B. \(f\left( a \right) \ge 0.\)
C. \(f\left( a \right) = 0.\)
D. \(f\left( a \right) > 0.\)
Câu 7: Giải phương trình \(\sqrt {2{x^2} – 8x + 4} = x – 2\).
A. \(x = 4\).
B. \(\left[ \begin{array}{l}x = 0\\x = 4\end{array} \right.\).
C. \(x = 4 + 2\sqrt 2 \).
D. \(x = 6\).
Câu 8: Số nghiệm nguyên âm của phương trình: \(\sqrt {{x^2} + 3x – 2} = \sqrt {1 + x} \) là
A. \(3\). B. \(2\). C. \(0\). D. \(1\).
Câu 9: Cho đường thẳng \(\left( d \right):2x + 3y – 4 = 0\). Vectơ nào sau đây là vectơ pháp tuyến của \(\left( d \right)?\)
A. \(\overrightarrow {{n_1}} = \left( {3;2} \right)\).
B. \(\overrightarrow {{n_2}} = \left( { – 4; – 6} \right)\).
C. \(\overrightarrow {{n_3}} = \left( {2; – 3} \right)\).
D. \(\overrightarrow {{n_4}} = \left( { – 2;3} \right)\).
Câu 10: Đường thẳng đi qua \(A\left( { – 1;{\rm{ }}2} \right)\), nhận \(\overrightarrow n = (2; – 4)\) làm véctơ pháp tuyến có phương trình là:
A. \(-x + 2y-4 = 0\).
B. \(x-2y + 5 = 0\).
C. \(x-2y-4 = 0\).
D. \(x + y + 4 = 0\).
Câu 11: Cho đường thẳng \(d:x – 2y + 1 = 0\). Nếu đường thẳng \(\Delta \) qua điểm \(M\left( {1; – 1} \right)\) và \(\Delta \) song song với \(d\) thì \(\Delta \) có phương trình:
A. \(x – 2y – 3 = 0.\)
B. \(x – 2y + 5 = 0.\)
C. \(x – 2y + 3 = 0.\)
D. \(x + 2y + 1 = 0.\)
Câu 12: Khoảng cách từ điểm \(M\left( {1\,;\, – 1} \right)\) đến đường thẳng \(\Delta :\,3x – 4y – 17 = 0\) là:
A. \(\frac{2}{5}\). B. \(2\). C. \(\frac{{18}}{5}\). D. \(\frac{{10}}{{\sqrt 5 }}\).
Câu 13: Tính góc giữa hai đường thẳng: \(3x + y – 1 = 0\) và \(4x – 2y – 4 = 0\).
A. \({30^0}\). B. \({60^0}\). C. \({90^0}\). D. \({45^0}\).
Câu 14: Tìm điểm \(M\) trên trục \(Ox\) sao cho nó cách đều hai đường thẳng: \({d_1}:\,3x + 2y – 6 = 0\)
và \({d_2}:\,3x + 2y + 6 = 0\)?
A. \(\left( {1\,;\,0} \right)\).
B. \(\left( {0\,;\,0} \right)\).
C. \(\left( {0\,;\,\sqrt 2 } \right)\).
D. \(\left( {\sqrt 2 \,;\,0} \right)\).
Câu 15: Đường tròn tâm \(I\left( {a;b} \right)\) và bán kính \(R\) có dạng:
A. \({\left( {x + a} \right)^2} + {\left( {y + b} \right)^2} = {R^2}\).
B. \({\left( {x – a} \right)^2} + {\left( {y – b} \right)^2} = {R^2}\).
C. \({\left( {x – a} \right)^2} + {\left( {y + b} \right)^2} = {R^2}\).
D. \({\left( {x + a} \right)^2} + {\left( {y – b} \right)^2} = {R^2}\).
Câu 16: Đường tròn \({x^2} + {y^2} – 10x – 11 = 0\) có bán kính bằng bao nhiêu?
A. \(6\). B. \(2\). C. \(36\). D. \(\sqrt 6 \).
Câu 17: Phương trình tiếp tuyến \(d\) của đường tròn \(\left( C \right):{\left( {x + 2} \right)^2} + {\left( {y + 2} \right)^2} = 25\) tại điểm \(M\left( {2;1} \right)\) là:
A. \(d: – y + 1 = 0.\)
B. \(d:4x + 3y + 14 = 0.\)
C. \(d:3x – 4y – 2 = 0.\)
D. \(d:4x + 3y – 11 = 0.\)
Câu 18: Với những giá trị nào của \(m\) thì đường thẳng \(\Delta :4x + 3y + m = 0\) tiếp xúc với đường tròn \(\left( C \right):{x^2} + {y^2} – 9 = 0\).
A. \(m = – 3\).
B. \(m = 3\) và \(m = – 3\).
C. \(m = 3\).
D. \(m = 15\) và \(m = – 15\).
Câu 19: Phương trình của đường Elip có dạng chính tắc là
A. \(\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1.\)
B. \(\frac{{{x^2}}}{{{a^2}}} – \frac{{{y^2}}}{{{b^2}}} = 1\).
C. \(\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 0.\)
D. \(\frac{{{x^2}}}{{{a^2}}} – \frac{{{y^2}}}{{{b^2}}} = 0.\)
Câu 20: Phương trình chính tắc của parabol \(\left( P \right)\) có tiêu điểm \(F\left( {\frac{3}{2};0} \right)\) là
A. \({y^2} = \frac{3}{2}x\).
B. \({y^2} = 3x\).
C. \({y^2} = 6x\).
D. \({y^2} = \frac{3}{4}x\).
Câu 21: Bạn An có 4 chiếc mũ khác nhau và 3 áo khoác khác nhau để sử dụng khi đi học. Hỏi bạn An có bao nhiêu cách chọn 1 chiếc mũ và 1 áo khoác để sử dụng khi đi học?
A. 12. B. 7. C. 1. D. 3.
Câu 22: Từ tập \(\left\{ {1;2;3;4;5} \right\}\) lập được bao nhiêu số tự nhiên chẵn có hai chữ số.
A. \(5\). B. \(25\). C. \(8\). D. \(10\).
Câu 23: Có 3 bông hoa trắng, 2 bông hoa đỏ và 4 bông hoa tím. Hỏi có bao nhiêu cách chọn ra 2 bông hoa có màu khác nhau.
A. \(26\). B. \(36\). C. \(24\). D. \(9\).
Câu 24: Có bao nhiêu cách xếp 4 lá thư khác nhau vào 4 chiếc phong bì khác nhau (mỗi lá thư là một phong bì)?
A. \(12\). B. \(4!\). C. \(P_4^2\). D. \(3!\).
Câu 25: Có bao nhiêu cách xếp khác nhau cho 4 người ngồi vào 6 chỗ trên một bàn dài?
A. \(15.\) B. \(720.\) C. \(30.\) D. \(360.\)
Câu 26: Cho \(15\) điểm trên cùng một mặt phẳng sao cho không có ba điểm nào thẳng hàng. Có bao nhiêu tam giác có cả ba đỉnh là 3 trong số 15 điểm đã cho?
A. \(3375\). B. \(2730\). C. \(455\). D. \(45\).
Câu 27: Cho tập hợp \(A = \left\{ {1,2,3,4,5,6,7,8} \right\}\). Từ tập hợp \(A\) lập được bao nhiêu số có năm chữ số đôi một khác nhau và luôn có mặt chữ số \(2\).
A. \(4200\). B. \(175\). C. \(8400\). D. \(6720\).
Câu 28: Có bao nhiêu cách xếp \(5\) sách Văn khác nhau và \(7\) sách Toán khác nhau trên một kệ sách dài nếu các sách Văn phải xếp kề nhau?
A. \(2.5!.7!\). B. \(5!.8!\). C. \(12!\). D. \(5!.7!\).
Câu 29: Trong khai triển của nhị thức \({\left( {3{x^2} – y} \right)^4}\)chứa số hạng \(54{x^4}{y^k}\) thì giá trị của \(k\) là
A. \(2\). B. \(1\). C. \(3\). D. \(4\).
Câu 30: Gieo một đồng tiền liên tiếp 2 lần. Số phần tử của không gian mẫu \(n\left( \Omega \right)\) là
A. 8. B. 1. C. 2. D. 4.
Câu 31: Gieo một đồng tiền và một con súc sắc. Số phần tử của không gian mẫu là
A. 12. B. 6. C. 8. D. 24.
Câu 32: Cho phép thử có không gian mẫu . Các cặp biến cố không đối nhau là
A. \(A = \left\{ 1 \right\}\) và \(B = \left\{ {2,\,3,\,4,\,5,\,6} \right\}\).
B. \(C\left\{ {1,\,4,\,5} \right\}\) và \(D = \left\{ {2,\,3,\,6} \right\}\).
C. \(E = \left\{ {1,\,4,\,6} \right\}\) và \(F = \left\{ {2,\,3} \right\}\).
D. \(\Omega \) và \(\emptyset \).
Câu 33: Từ một hộp chứa ba quả cầu trắng và hai quả cầu đen lấy ngẫu nhiên hai quả. Xác suất để lấy được cả hai quả trắng là
A. \(\frac{6}{{30}}\). B. \(\frac{{12}}{{30}}\). C. \(\frac{{10}}{{30}}\). D. \(\frac{9}{{30}}\).
Câu 34: Rút một lá bài từ bộ bài gồm 52 lá. Xác suất để được lá bích là
A. \(\frac{1}{4}.\) B. \(\frac{{12}}{{13}}.\) C. \(\frac{3}{4}.\) D. \(\frac{1}{{13}}.\)
Câu 35: Có 9 chiếc thẻ được đánh số từ 1 đến 9, người ta rút ngẫu nhiên hai thẻ khác nhau. Xác suất để rút được hai thẻ mà tích hai số được đánh trên thẻ là số chẵn bằng
A. \(\frac{{13}}{{18}}\). B. \(\frac{5}{{18}}\). C. \(\frac{1}{3}\). D. \(\frac{2}{3}\).
II. TỰ LUẬN (04 câu – 3,0 điểm)
Câu 36: Khi một quả bóng được đá lên, nó sẽ đạt đến độ cao nào đó rồi rơi xuống. Biết rằng quỹ đạo của quả bóng là một cung parabol trong mặt phẳng với hệ tọa độ \(Oth,\) trong đó \(t\) là thời gian (tính bằng giây) kể từ khi quả bóng được đá lên; \(h\) là độ cao (tính bằng mét) của quả bóng. Giả thiết rằng quả bóng được đá lên từ độ cao \(1,2m\). Sau đó \(1\) giây, nó đạt độ cao \(8,5m\)và \(2\) giây sau khi đá lên, nó đạt độ cao \(6m\). Hỏi sau bao lâu thì quả bóng sẽ chạm đất kể từ khi được đá lên (tính chính xác đến hàng phần trăm)?
Câu 37: Trong mặt phẳng tọa độ \(Oxy\), cho tam giác \(ABC\) vuông cân tại \(A\) có phương trình đường thẳng \(AB\) là \(2x – y – 5 = 0\), điểm \(M\left( {1;2} \right)\) nằm trên đường thẳng \(BC\). Phương trình đường thẳng \(BC\) là
Câu 38: Gia chủ có một miếng đất có hình Elip với độ dài trục lớn bằng \({\rm{2}}\sqrt 3 {\rm{ m}}\), độ dài trục nhỏ bằng \({\rm{2 m}}\). Gia chủ muốn trồng hoa thành hình tam giác cân \(OAB\) (tham khảo hình vẽ) với điểm \(O\) là tâm của Elip, các điểm \(A\) và \(B\) thuộc đường Elip nói trên.

Diện tích trồng hoa lớn nhất bằng
Câu 39: Từ các chữ số \(2,3,4,5,6,7\) lập được bao nhiêu số tự nhiên có \(6\)chữ số khác nhau và tổng ba chữ số đầu nhỏ hơn tổng ba chữ số sau 1 đơn vị?
———- HẾT ———-
Đáp án Đề thi:
HƯỚNG DẪN GIẢI CHI TIẾT
THỰC HIỆN: BAN CHYÊN MÔN GiaiBaitapsgk.COM
I. PHẦN TRẮC NGHIỆM (35 câu – 7,0 điểm).
Câu 1: Tìm \(m\) để hàm số \(y = \left( {2m + 1} \right)x + m – 3\) đồng biến trên \(R\)
A. \(m > \frac{1}{2}.\) B. \(m < \frac{1}{2}.\) C. \(m < – \frac{1}{2}.\) D. \(m > – \frac{1}{2}.\)
Phương pháp
– Hàm số \(y = ax + b,a \ne 0\) đồng biến trên R khi a > 0
Lời giải
Chọn D
Hàm số \(y = \left( {2m + 1} \right)x + m – 3\) đồng biến trên R \( \Leftrightarrow 2m + 1 > 0 \Leftrightarrow m > – \frac{1}{2}.\)
Câu 2: Tập xác định của hàm số \(y = \sqrt {x – 3} + \frac{1}{{x – 3}}\) là
A \(D = \mathbb{R}\backslash \left\{ 3 \right\}\).
B. \(D = \left[ {3; + \infty } \right)\).
C. \(D = \left( {3; + \infty } \right)\).
D. \(D = \left( { – \infty ;3} \right)\).
Phương pháp
– Phân thức xác định khi mẫu thức khác 0
– Căn thức xác định khi biểu thức trong căn lớn hơn bằng 0
Lời giải
Chọn D
Hàm số xác định khi \(\left\{ \begin{array}{l}x – 3 \ge 0\\x – 3 \ne 0\end{array} \right. \Leftrightarrow x > 3\).
Vậy TXĐ: \(D = \left( {3; + \infty } \right)\).
Câu 3: Parabol \(y = – 2{x^2} + 3x – 1\) có tọa độ đỉnh I là:
A. \(\left( {\frac{3}{4};\frac{1}{8}} \right).\)
B. \(\left( { – \frac{3}{2}; – 10} \right).\)
C. \(\left( {\frac{3}{2}; – 1} \right).\)
D. \(\left( {\frac{3}{4};\frac{{17}}{8}} \right).\)
Phương pháp
Tọa độ đỉnh của Parabol là \(I\left( { – \frac{b}{{2a}}; – \frac{\Delta }{{4a}}} \right)\)
Lời giải
Chọn A
\( – \frac{b}{{2a}} = \frac{3}{4}\) và \( – \frac{\Delta }{{4a}} = \frac{1}{8}\) \( \Rightarrow \) Parabol có đỉnh \(I\left( {\frac{3}{4};\frac{1}{8}} \right)\)
Câu 4: Tìm parabol \(\left( P \right):y = a{x^2} + 3x – 2,\) biết rằng parabol có trục đối xứng \(x = – 3\)?
A. \(y = {x^2} + 3x – 2.\)
B. \(y = \frac{1}{2}{x^2} + x – 2.\)
C. \(y = \frac{1}{2}{x^2} + 3x – 3.\)
D. \(y = \frac{1}{2}{x^2} + 3x – 2.\)
Phương pháp
Trục đối xứng của \(\left( P \right):y = a{x^2} + bx + c\) là \(x = \frac{{ – b}}{{2a}}\)
Lời giải
Chọn D
Ta có trục đối xứng của \(\left( P \right):y = a{x^2} + 3x – 2\) là \(x = \frac{{ – 3}}{{2a}} = – 3 \Leftrightarrow a = \frac{1}{2}\)
Vậy \(\left( P \right):y = \frac{1}{2}{x^2} + 3x – 2.\)
Câu 5: Cho tam thức bậc hai \(f(x) = 5x – {x^2} – 6\). Tìm \(x\) để \(f(x) \ge 0\).
A. \(x \in \left( { – \infty ;2} \right] \cup \left[ {3; + \infty } \right)\).
B. \(x \in \left[ {2;3} \right]\).
C. \(x \in \left( { – \infty ;2} \right) \cup \left( {3; + \infty } \right)\).
D. \(x \in \left( {2;3} \right)\).
Phương pháp
Sử dụng dấu của tam thức bậc hai
Lời giải
Chọn B
Ta có thể viết \(f\left( x \right) = – {x^2} + 5x – 6\).
\( – {x^2} + 5x – 6 = 0 \Leftrightarrow \left[ \begin{array}{l}x = 2\\x = 3\end{array} \right.\)
Ta có bảng xét dấu

Vậy \(f(x) \ge 0 \Leftrightarrow x \in \left[ {2;3} \right]\).
Câu 6: Cho tam thức bậc hai \(f\left( x \right) = {x^2} – 5x + 6\) và a là số thực lớn hơn 3. Tìm khẳng định đúng trong các khẳng định sau.
A. \(f\left( a \right) < 0.\)
B. \(f\left( a \right) \ge 0.\)
C. \(f\left( a \right) = 0.\)
D. \(f\left( a \right) > 0.\)
Phương pháp
Sử dụng dấu của tam thức bậc hai
Lời giải
Chọn D.
Xét phương trình \({x^2} – 5x + 6 = 0 \Leftrightarrow \left[ \begin{array}{l}x = 2\\x = 3\end{array} \right.\)
Ta có bảng xét dấu

Ta thấy \(f\left( x \right) > 0,\forall x \in \left( {3; + \infty } \right)\)
Vậy a là số thực lớn hơn 3 thì \(f\left( a \right) > 0.\)
Câu 7: Giải phương trình \(\sqrt {2{x^2} – 8x + 4} = x – 2\).
A. \(x = 4\).
B. \(\left[ \begin{array}{l}x = 0\\x = 4\end{array} \right.\).
C. \(x = 4 + 2\sqrt 2 \).
D. \(x = 6\).
Phương pháp
Bình phương hai vế của phương trình
Lời giải
Chọn A.
\(\sqrt {2{x^2} – 8x + 4} = x – 2\)\( \Leftrightarrow \left\{ \begin{array}{l}x – 2 \ge 0\\2{x^2} – 8x + 4 = {\left( {x – 2} \right)^2}\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}x \ge 2\\\left[ \begin{array}{l}x = 0\,\\x = 4\,\end{array} \right.\end{array} \right.\)\( \Leftrightarrow x = 4\).
Câu 8: Số nghiệm nguyên âm của phương trình: \(\sqrt {{x^2} + 3x – 2} = \sqrt {1 + x} \) là
A. \(3\). B. \(2\). C. \(0\). D. \(1\).
Phương pháp
Bình phương hai vế của phương trình
Lời giải
Chọn D
\(\sqrt {{x^2} + 3x – 2} = \sqrt {1 + x} \)\( \Leftrightarrow \left\{ \begin{array}{l}1 + x \ge 0\\{x^2} + 3x – 2 = 1 + x\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}x \ge – 1\\{x^2} + 2x – 3 = 0\end{array} \right. \Leftrightarrow x = 1\).
Câu 9: Cho đường thẳng \(\left( d \right):2x + 3y – 4 = 0\). Vectơ nào sau đây là vectơ pháp tuyến của \(\left( d \right)?\)
A. \(\overrightarrow {{n_1}} = \left( {3;2} \right)\).
B. \(\overrightarrow {{n_2}} = \left( { – 4; – 6} \right)\).
C. \(\overrightarrow {{n_3}} = \left( {2; – 3} \right)\).
D. \(\overrightarrow {{n_4}} = \left( { – 2;3} \right)\).
Phương pháp
Phương trình đường thẳng \(d:ax + by + c = 0\)có VTPT là \(\overrightarrow n = (a;b).\)
Lời giải
Chọn B
\(\overrightarrow n = \left( {2;3} \right)\), ta có \(\frac{{ – 4}}{2} = \frac{{ – 6}}{3} \Rightarrow {\overrightarrow n _2}\) là VTPT của \(\left( d \right)\)
Câu 10: Đường thẳng đi qua \(A\left( { – 1;{\rm{ }}2} \right)\), nhận \(\overrightarrow n = (2; – 4)\) làm véctơ pháp tuyến có phương trình là:
A. \(-x + 2y-4 = 0\).
B. \(x-2y + 5 = 0\).
C. \(x-2y-4 = 0\).
D. \(x + y + 4 = 0\).
Phương pháp
Phương trình đường thẳng đi qua \(M\left( {{x_0};{y_0}} \right)\)có véc tơ pháp tuyến \(\overrightarrow n = \left( {a;b} \right)\)là
\(a\left( {x – {x_0}} \right) + b\left( {y – {y_0}} \right) = 0\).
Lời giải
Chọn B.
Đường thẳng đi qua \(A\left( { – 1;{\rm{ }}2} \right)\), nhận \(\overrightarrow n = (2; – 4)\) làm véctơ pháp tuyến có phương trình là:
\(2\left( {x + 1} \right) – 4\left( {y – 2} \right) = 0 \Leftrightarrow x – 2y + 5 = 0\).
Câu 11: Cho đường thẳng \(d:x – 2y + 1 = 0\). Nếu đường thẳng \(\Delta \) qua điểm \(M\left( {1; – 1} \right)\) và \(\Delta \) song song với \(d\) thì \(\Delta \) có phương trình:
A. \(x – 2y – 3 = 0.\) B. \(x – 2y + 5 = 0.\) C. \(x – 2y + 3 = 0.\) D. \(x + 2y + 1 = 0.\)
Phương pháp
Phương trình đường thẳng đi qua \(M\left( {{x_0};{y_0}} \right)\)có véc tơ pháp tuyến \(\overrightarrow n = \left( {a;b} \right)\)là
\(a\left( {x – {x_0}} \right) + b\left( {y – {y_0}} \right) = 0\).
Lời giải
Chọn A.
\(D\) có véc tơ pháp tuyến là \(\overrightarrow n = \left( {1; – 2} \right)\).
\(d\) qua \(M\left( {1; – 1} \right)\) và \(d{\rm{//}}D\) nên \(d:{\rm{ }}1\left( {x – 1} \right) – 2\left( {y + 1} \right) = 0 \Leftrightarrow x – 2y – 3 = 0\).
Câu 12: Khoảng cách từ điểm \(M\left( {1\,;\, – 1} \right)\) đến đường thẳng \(\Delta :\,3x – 4y – 17 = 0\) là:
A. \(\frac{2}{5}\). B. \(2\). C. \(\frac{{18}}{5}\). D. \(\frac{{10}}{{\sqrt 5 }}\).
Phương pháp
Khoảng cách từ điểm \(M({x_0};{y_0})\) đến đường thẳng \(\Delta :{\rm{ }}ax + by + c = 0\) là: \(d(M,\Delta ) = \frac{{\left| {a{x_0} + b{y_0} + c} \right|}}{{\sqrt {{a^2} + {b^2}} }}\)
Lời giải
Chọn B.
Ta có \(d\left( {M,\,\Delta } \right) = \frac{{\left| {3.1 – 4.\left( { – 1} \right) – 17} \right|}}{{\sqrt {{3^2} + {{\left( { – 4} \right)}^2}} }} = 2\).
Câu 13: Tính góc giữa hai đường thẳng: \(3x + y – 1 = 0\) và \(4x – 2y – 4 = 0\).
A. \({30^0}\). B. \({60^0}\). C. \({90^0}\). D. \({45^0}\).
Phương pháp
Áp dụng công thức tính góc giữa hai đường thẳng có: \(\cos \left( {{d_1},{d_2}} \right) = \frac{{\overrightarrow {{n_1}} .\overrightarrow {{n_2}} }}{{\left| {\overrightarrow {{n_1}} } \right|.\left| {\overrightarrow {{n_2}} } \right|}}\).
Lời giải
Chọn D.
Đường thẳng: \(3x + y – 1 = 0\) có véctơ pháp tuyến \(\overrightarrow {{n_1}} = \left( {3\,;\,1} \right)\)
Đường thẳng: \(4x – 2y – 4 = 0\) có véctơ pháp tuyến \(\overrightarrow {{n_2}} = \left( {4\,;\, – 2} \right)\)
\(\cos \left( {{d_1};{d_2}} \right) = \left| {\cos \left( {\overrightarrow {{n_1}} ;\overrightarrow {{n_2}} } \right)} \right| = \frac{{\left| {\overrightarrow {{n_1}} .\overrightarrow {{n_2}} } \right|}}{{\left| {\overrightarrow {{n_1}} } \right|.\left| {\overrightarrow {{n_2}} } \right|}} = \frac{1}{{\sqrt 2 }}\;\; \Rightarrow \left( {{d_1};{d_2}} \right) = {45^0}\).
Câu 14: Tìm điểm \(M\) trên trục \(Ox\) sao cho nó cách đều hai đường thẳng: \({d_1}:\,3x + 2y – 6 = 0\)
và \({d_2}:\,3x + 2y + 6 = 0\)?
A. \(\left( {1\,;\,0} \right)\).
B. \(\left( {0\,;\,0} \right)\).
C. \(\left( {0\,;\,\sqrt 2 } \right)\).
D. \(\left( {\sqrt 2 \,;\,0} \right)\).
Phương pháp
Khoảng cách từ điểm \(M({x_0};{y_0})\) đến đường thẳng \(\Delta :{\rm{ }}ax + by + c = 0\) là: \(d(M,\Delta ) = \frac{{\left| {a{x_0} + b{y_0} + c} \right|}}{{\sqrt {{a^2} + {b^2}} }}\)
Lời giải
Chọn B.
Gọi \(M\left( {a\,;\,0} \right) \in Ox\; \Rightarrow \left| {3a – 6} \right| = \left| {3a + 6} \right| \Leftrightarrow a = 0\; \Rightarrow M\left( {0\,;\,0} \right)\).
Câu 15: Đường tròn tâm \(I\left( {a;b} \right)\) và bán kính \(R\) có dạng:
A. \({\left( {x + a} \right)^2} + {\left( {y + b} \right)^2} = {R^2}\).
B. \({\left( {x – a} \right)^2} + {\left( {y – b} \right)^2} = {R^2}\).
C. \({\left( {x – a} \right)^2} + {\left( {y + b} \right)^2} = {R^2}\).
D. \({\left( {x + a} \right)^2} + {\left( {y – b} \right)^2} = {R^2}\).
Phương pháp
Phương trình đường tròn (O) có tâm I(a,b) và bán kính R là : \({(x – a)^2} + {(y – b)^2} = {R^2}\)
Lời giải
Chọn B
Theo định nghĩa đường tròn tâm \(I\left( {a;b} \right)\) và bán kính \(R\) có dạng: \({\left( {x – a} \right)^2} + {\left( {y – b} \right)^2} = {R^2}\)
Câu 16: Đường tròn \({x^2} + {y^2} – 10x – 11 = 0\) có bán kính bằng bao nhiêu?
A. \(6\). B. \(2\). C. \(36\). D. \(\sqrt 6 \).
Phương pháp
Phương trình tổng quát của đường tròn có dạng: \({x^2} + {y^2} – 2ax – 2by + c = 0\) với \(I\left( {a;\,\,b} \right)\) là tâm và bán kính được tính bằng công thức \(R = \sqrt {{a^2} + {b^2} – c} \)
Lời giải
Chọn A.
Ta có I(5;0) và
Suy ra bán kinh \(R = \sqrt {{a^2} + {b^2} + {c^2}} = \sqrt {{5^2} + {0^2} + 11} = 6\).
Câu 17: Phương trình tiếp tuyến \(d\) của đường tròn \(\left( C \right):{\left( {x + 2} \right)^2} + {\left( {y + 2} \right)^2} = 25\) tại điểm \(M\left( {2;1} \right)\) là:
A. \(d: – y + 1 = 0.\)
B. \(d:4x + 3y + 14 = 0.\)
C. \(d:3x – 4y – 2 = 0.\)
D. \(d:4x + 3y – 11 = 0.\)
Phương pháp
Phương trình đường thẳng đi qua \(M\left( {{x_0};{y_0}} \right)\)có véc tơ pháp tuyến \(\overrightarrow n = \left( {a;b} \right)\)là
\(a\left( {x – {x_0}} \right) + b\left( {y – {y_0}} \right) = 0\).
Lời giải
Chọn D.
Đường tròn (C) có tâm \(I\left( { – 2; – 2} \right)\) nên tiếp tuyến tại M có VTPT là \(\vec n = \overrightarrow {IM} = \left( {4;3} \right),\) nên có phương trình là: \(4\left( {x – 2} \right) + 3\left( {y – 1} \right) = 0 \Leftrightarrow 4x + 3y – 11 = 0.\)
Câu 18:
Với những giá trị nào của \(m\) thì đường thẳng \(\Delta :4x + 3y + m = 0\) tiếp xúc với đường tròn \(\left( C \right):{x^2} + {y^2} – 9 = 0\).
A. \(m = – 3\).
B. \(m = 3\) và \(m = – 3\).
C. \(m = 3\).
D. \(m = 15\) và \(m = – 15\).
Phương pháp
Khoảng cách từ điểm \(M({x_0};{y_0})\) đến đường thẳng \(\Delta :{\rm{ }}ax + by + c = 0\) là: \(d(M,\Delta ) = \frac{{\left| {a{x_0} + b{y_0} + c} \right|}}{{\sqrt {{a^2} + {b^2}} }}\)
Lời giải
Chọn D.
Do đường tròn tiếp xúc với đường thẳng \(\Delta \) nên \(R = d\left( {I,\Delta } \right) = \frac{{\left| {4.0 + 3.0 + m} \right|}}{{\sqrt {{4^2} + {3^2}} }} = 3 \Leftrightarrow m = \pm 15\).
Câu 19: Phương trình của đường Elip có dạng chính tắc là
A. \(\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1.\)
B. \(\frac{{{x^2}}}{{{a^2}}} – \frac{{{y^2}}}{{{b^2}}} = 1\).
C. \(\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 0.\)
D. \(\frac{{{x^2}}}{{{a^2}}} – \frac{{{y^2}}}{{{b^2}}} = 0.\)
Phương pháp
Phương trình Elip \(\left( E \right):\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1\)
Lời giải
Chọn A.
Phương trình Elip \(\left( E \right):\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1\)
Câu 20: Phương trình chính tắc của parabol \(\left( P \right)\) có tiêu điểm \(F\left( {\frac{3}{2};0} \right)\) là
A. \({y^2} = \frac{3}{2}x\).
B. \({y^2} = 3x\).
C. \({y^2} = 6x\).
D. \({y^2} = \frac{3}{4}x\).
Phương pháp
Tọa độ tiêu điểm của Parabol \(\left( P \right):\,{y^2} = 2px\) là \(F\left( {\frac{p}{2};0} \right)\)
Lời giải
Chọn C.
Parabol \(\left( P \right)\) có tiêu điểm \(F\left( {\frac{3}{2};0} \right)\) \( \Rightarrow p = 3\). Vậy phương trình chính tắc của parabol là \({y^2} = 6x\).
Câu 21: Bạn An có 4 chiếc mũ khác nhau và 3 áo khoác khác nhau để sử dụng khi đi học. Hỏi bạn An có bao nhiêu cách chọn 1 chiếc mũ và 1 áo khoác để sử dụng khi đi học?
A. 12. B. 7. C. 1. D. 3.
Phương pháp
Áp dụng quy tắc nhân
Lời giải
Chọn A.
Công việc được hoàn thành bởi 2 hành động liên tiếp:
Hành động 1. Chọn 1 chiếc mũ: có 4 cách chọn.
Hành động 2. Chọn 1 áo khoác: có 3 cách chọn.
Áp dụng quy quy tắc nhân, suy ra có \(4 \cdot 3 = 12\) cách.
Câu 22: Từ tập \(\left\{ {1;2;3;4;5} \right\}\) lập được bao nhiêu số tự nhiên chẵn có hai chữ số.
A. \(5\). B. \(25\). C. \(8\). D. \(10\).
Phương pháp
Áp dụng quy tắc nhân
Lời giải
Chọn D
Gọi số tự nhiên thỏa mãn yêu cầu bài toán là \(\overline {ab} \).
Chọn \(b\) có 2 cách;
Chọn \(a\) có 5 cách;
Suy ra có 10 số.
Câu 23: Có 3 bông hoa trắng, 2 bông hoa đỏ và 4 bông hoa tím. Hỏi có bao nhiêu cách chọn ra 2 bông hoa có màu khác nhau.
A. \(26\). B. \(36\). C. \(24\). D. \(9\).
Phương pháp
Áp dụng quy tắc nhân
Lời giải
Chọn A.
TH1: 1 hoa trắng và 1 hoa đỏ:
Chọn 1 hoa trắng: có 3 cách.
Chọn 1 hoa đỏ: có 2 cách.
Vậy có \(3.2 = 6\) cách.
TH2: 1 hoa trắng và 1 hoa tím:
Chọn 1 hoa trắng: có 3 cách.
Chọn 1 hoa tím: có 4 cách.
Vậy có \(3.4 = 12\) cách.
TH3: 1 hoa đỏ và 1 hoa tím:
Chọn 1 hoa đỏ: có 2 cách.
Chọn 1 hoa tím: có 4 cách.
Vậy có \(2.4 = 8\) cách.
Áp dụng qui tắc cộng, ta có \(6 + 12 + 8 = 26\) cách.
Câu 24: Có bao nhiêu cách xếp 4 lá thư khác nhau vào 4 chiếc phong bì khác nhau (mỗi lá thư là một phong bì)?
A. \(12\). B. \(4!\). C. \(P_4^2\). D. \(3!\).
Phương pháp
Áp dụng quy tắc hoán vị
Lời giải
Chọn B
Mỗi cách xếp 4 lá thư khác nhau vào 4 chiếc phong bì khác nhau (mỗi lá thư là một phong bì) là một hoán vị của 4 phần tử.
Do đó số cách xếp là \(4! = 24\) cách.
Câu 25: Có bao nhiêu cách xếp khác nhau cho 4 người ngồi vào 6 chỗ trên một bàn dài?
A. \(15.\) B. \(720.\) C. \(30.\) D. \(360.\)
Phương pháp
Áp dụng công thức chỉnh hợp
Lời giải
Chọn D
Số cách xếp khác nhau cho 4 người ngồi vào 6 chỗ trên một bàn dài là số chỉnh hợp chập 4 của 6 phần tử. Suy ra có \(A_6^4 = 360\) cách.
Câu 26: Cho \(15\) điểm trên cùng một mặt phẳng sao cho không có ba điểm nào thẳng hàng. Có bao nhiêu tam giác có cả ba đỉnh là 3 trong số 15 điểm đã cho?
A. \(3375\). B. \(2730\). C. \(455\). D. \(45\).
Phương pháp
Áp dụng công thức tổ hợp
Lời giải
Chọn C
Số tam giác thỏa mãn yêu cầu bài toán là \(C_{15}^3 = 455\).
Câu 27: Cho tập hợp \(A = \left\{ {1,2,3,4,5,6,7,8} \right\}\). Từ tập hợp \(A\) lập được bao nhiêu số có năm chữ số đôi một khác nhau và luôn có mặt chữ số \(2\).
A. \(4200\). B. \(175\). C. \(8400\). D. \(6720\).
Phương pháp
Áp dụng công thức chỉnh hợp
Lời giải
Chọn A
Gọi số có \(5\) chữ số khác nhau được lập từ \(A\) và luôn có mặt chữ số \(2\) là \(\overline {abcde} \).
Có \(5\) vị trí cho chữ số 2
Sau khi chọn vị trí cho chữ số \(2\) có \(A_7^4\) cách chọn và sắp xếp \(4\)chữ số còn lại.
Theo quy tắc nhân ta có \(5.A_7^4 = 4200\) số.
Câu 28: Có bao nhiêu cách xếp \(5\) sách Văn khác nhau và \(7\) sách Toán khác nhau trên một kệ sách dài nếu các sách Văn phải xếp kề nhau?
A. \(2.5!.7!\). B. \(5!.8!\). C. \(12!\). D. \(5!.7!\).
Phương pháp
Áp dụng công thức hoán vị
Lời giải
Chọn B.
Ta xếp 5 cuốn sách Văn kề nhau có \(5!\) cách sắp xếp. Lúc này xem 5 cuốn sách Văn là 1 vị trí và xếp cùng với 7 cuốn sách Toán sắp xếp vào 8 vị trí trên kệ sách sẽ có \(8!\) cách.
Vậy theo quy tắc nhân ta có \(5!.8!\) cách sắp xếp.
Câu 29: Trong khai triển của nhị thức \({\left( {3{x^2} – y} \right)^4}\)chứa số hạng \(54{x^4}{y^k}\) thì giá trị của \(k\) là
A. \(2\). B. \(1\). C. \(3\). D. \(4\).
Phương pháp
Áp dụng công thức khai triển nhị thức newton.
Lời giải
Chọn A.
Ta có:
\(\begin{array}{l}{\left( {3{x^2} – y} \right)^4} = C_4^0{\left( {3{x^2}} \right)^4} + C_4^1{\left( {3{x^2}} \right)^3}\left( { – y} \right) + C_4^2{\left( {3{x^2}} \right)^2}{\left( { – y} \right)^2} + C_4^3\left( {3{x^2}} \right){\left( { – y} \right)^3} + C_4^4{\left( { – y} \right)^4}\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = 81{x^8} – 108{x^6}y + 54{x^4}{y^2} – 12{x^2}{y^3} + {y^4}\end{array}\).
Vậy giá trị \(k = 2\).
Câu 30: Gieo một đồng tiền liên tiếp 2 lần. Số phần tử của không gian mẫu \(n\left( \Omega \right)\) là
A. 8. B. 1. C. 2. D. 4.
Phương pháp
Áp dụng quy tắc đếm
Lời giải
Chọn D
\(n\left( \Omega \right) = 2.2 = 4\).
(lần 1 có 2 khả năng xảy ra; lần 2 có 2 khả năng xảy ra).
Câu 31: Gieo một đồng tiền và một con súc sắc. Số phần tử của không gian mẫu là
A. 12. B. 6. C. 8. D. 24.
Phương pháp
Áp dụng quy tắc đếm
Lời giải
Chọn A
Mô tả không gian mẫu ta có: \(\Omega = \left\{ {S1;\,S2;\,S3;\,S4;\,S5;S6;N1;N2;N3;N4;N5;N6} \right\}\).
Câu 32: Cho phép thử có không gian mẫu . Các cặp biến cố không đối nhau là
A. \(A = \left\{ 1 \right\}\) và \(B = \left\{ {2,\,3,\,4,\,5,\,6} \right\}\).
B. \(C\left\{ {1,\,4,\,5} \right\}\) và \(D = \left\{ {2,\,3,\,6} \right\}\).
C. \(E = \left\{ {1,\,4,\,6} \right\}\) và \(F = \left\{ {2,\,3} \right\}\).
D. \(\Omega \) và \(\emptyset \).
Phương pháp
Áp dụng quy tắc đếm
Lời giải
Chọn C
Cặp biến cố không đối nhau là \(E = \left\{ {1,\,4,\,6} \right\}\) và \(F = \left\{ {2,\,3} \right\}\) do \(E \cap F = \emptyset \) và \(E \cup F \ne \Omega \).
Câu 33: Từ một hộp chứa ba quả cầu trắng và hai quả cầu đen lấy ngẫu nhiên hai quả. Xác suất để lấy được cả hai quả trắng là
A. \(\frac{6}{{30}}\). B. \(\frac{{12}}{{30}}\). C. \(\frac{{10}}{{30}}\). D. \(\frac{9}{{30}}\).
Phương pháp
Áp dụng công thức xác suất
Lời giải
Chọn D
\(n\left( \Omega \right) = C_5^2 = 10\). Gọi \(A\): “Lấy được hai quả màu trắng”.
Ta có \(n\left( A \right) = C_3^2 = 3\). Vậy \(P\left( A \right) = \frac{3}{{10}} = \frac{9}{{30}}\).
Câu 34: Rút một lá bài từ bộ bài gồm 52 lá. Xác suất để được lá bích là
A. \(\frac{1}{4}.\)
B. \(\frac{{12}}{{13}}.\)
C. \(\frac{3}{4}.\)
D. \(\frac{1}{{13}}.\)
Phương pháp
Áp dụng công thức xác suất
Lời giải
Chọn A
Bộ bài gồm có 13 lá bài bích. Vậy xác suất để lấy được lá bích là: \(P = \frac{{C_{13}^1}}{{C_{52}^1}} = \frac{{13}}{{52}} = \frac{1}{4}\).
Câu 35: Có 9 chiếc thẻ được đánh số từ 1 đến 9, người ta rút ngẫu nhiên hai thẻ khác nhau. Xác suất để rút được hai thẻ mà tích hai số được đánh trên thẻ là số chẵn bằng
A. \(\frac{{13}}{{18}}\). B. \(\frac{5}{{18}}\). C. \(\frac{1}{3}\). D. \(\frac{2}{3}\).
Phương pháp
Áp dụng công thức xác suất
Lời giải
Chọn A
Rút ra hai thẻ tùy ý từ 9 thẻ nên có \(n\left( \Omega \right) = C_9^2\)\( = 36\).
Gọi \(A\) là biến cố: “rút được hai thẻ mà tích hai số được đánh trên thẻ là số chẵn”
TH1: 1 thẻ đánh số lẻ, 1 thẻ đánh số chẵn có \(C_4^1.C_5^1 = 20\).
TH2: 2 thẻ đánh số chẵn có \(C_4^2 = 6\).
Suy ra \(n\left( A \right) = 26\).
Xác suất của \(A\) là: \(P\left( A \right) = \frac{{26}}{{36}}\)\( = \frac{{13}}{{18}}\).
II. TỰ LUẬN (04 câu – 3,0 điểm)
Câu 36: Khi một quả bóng được đá lên, nó sẽ đạt đến độ cao nào đó rồi rơi xuống. Biết rằng quỹ đạo của quả bóng là một cung parabol trong mặt phẳng với hệ tọa độ \(Oth,\) trong đó \(t\) là thời gian (tính bằng giây) kể từ khi quả bóng được đá lên; \(h\) là độ cao (tính bằng mét) của quả bóng. Giả thiết rằng quả bóng được đá lên từ độ cao \(1,2m\). Sau đó \(1\) giây, nó đạt độ cao \(8,5m\)và \(2\) giây sau khi đá lên, nó đạt độ cao \(6m\). Hỏi sau bao lâu thì quả bóng sẽ chạm đất kể từ khi được đá lên (tính chính xác đến hàng phần trăm)?
Phương pháp
Áp dụng công thức phương trình parabol
Lời giải
Gọi phương trình của parabol quỹ đạo là \(h = a{t^2} + bt + c\).
Từ giả thiết suy ra parabol đi qua các điểm \(\left( {0;1;2} \right)\), \(\left( {1;8;5} \right)\) và \(\left( {2;6} \right)\).
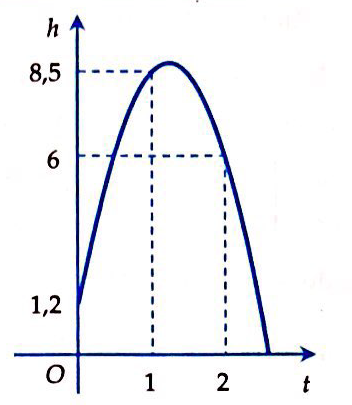
Từ đó ta có
\(\left\{ \begin{array}{l}c = 1,2\\a + b + c = 8,5\\4a + 2b + c = 6\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = – 4,9\\b = 12,2\\c = 1,2\end{array} \right.\).
Vậy phương trình của parabol quỹ đạo là \(h = – 4,9{t^2} + 12,2t + 1,2\).
Giải phương trình
\(h = 0 \Leftrightarrow – 4,9{t^2} + 12,2t + 1,2 = 0\) ta tìm được một nghiệm dương là \(t \approx 2,58\).
Câu 37: Trong mặt phẳng tọa độ \(Oxy\), cho tam giác \(ABC\) vuông cân tại \(A\) có phương trình đường thẳng \(AB\) là \(2x – y – 5 = 0\), điểm \(M\left( {1;2} \right)\) nằm trên đường thẳng \(BC\). Phương trình đường thẳng \(BC\) là
Phương pháp
Phương trình đường thẳng đi qua \(M\left( {{x_0};{y_0}} \right)\)có véc tơ pháp tuyến \(\overrightarrow n = \left( {a;b} \right)\)là
\(a\left( {x – {x_0}} \right) + b\left( {y – {y_0}} \right) = 0\).
Lời giải
Gọi \(\overrightarrow n = \left( {a;b} \right)\) \(({a^2} + {b^2} \ne 0)\)là một vectơ pháp tuyến của đường thẳng \(BC\), ta có \(\widehat {ABC} = 45^\circ \) nên suy ra \(\cos \left( {AB;BC} \right) = \frac{1}{{\sqrt 2 }}\).
Suy ra \(\frac{{\left| {2a – b} \right|}}{{\sqrt {5\left( {{a^2} + {b^2}} \right)} }} = \frac{1}{{\sqrt 2 }} \Leftrightarrow 2{\left( {2a – b} \right)^2} = 5\left( {{a^2} + {b^2}} \right)\)\( \Leftrightarrow 3{a^2} – 8ab – 3{b^2} = 0 \Leftrightarrow \left[ \begin{array}{l}a = 3b\\b = – 3a\end{array} \right.\).
+/ Với \(a = 3b\), chọn \(a = 3,b = 1\) ta có phương trình \(BC\) là: \(3x + y – 5 = 0\).
+/ Với \(b = – 3a\), chọn \(a = 1,b = – 3\) ta có phương trình \(BC\) là: \(x – 3y + 5 = 0\).
Câu 38: Gia chủ có một miếng đất có hình Elip với độ dài trục lớn bằng \({\rm{2}}\sqrt 3 {\rm{ m}}\), độ dài trục nhỏ bằng \({\rm{2 m}}\). Gia chủ muốn trồng hoa thành hình tam giác cân \(OAB\) (tham khảo hình vẽ) với điểm \(O\) là tâm của Elip, các điểm \(A\) và \(B\) thuộc đường Elip nói trên.

Diện tích trồng hoa lớn nhất bằng
Phương pháp
Phương trình Elip \(\left( E \right):\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1\)
Lời giải
Chọn hệ trục toạ độ như \(\left( {Oxy} \right)\) như hình vẽ.
Khi đó phương trình đường Elip là (E): \(\frac{{{x^2}}}{3} + \frac{{{y^2}}}{1} = 1.\)

Không mất tổng quát, ta chọn điểm \(A\) và \(B\) thuộc \(\left( E \right)\) sao cho điểm \(A\) và \(B\) có hoành độ dương. Do tam giác \(OAB\) cân tại \(O\) suy ra \(A\) đối xứng với \(B\) qua\(ox\).
Gọi điểm \(A\left( {{x_0};{y_o}} \right)\)\( \Rightarrow \)\(B\left( {{x_o}; – {y_o}} \right)\);\(\left( {{x_o} > 0} \right)\)
\(A \in \left( E \right):\frac{{x_0^2}}{3} + \frac{{y_0^2}}{1} = 1 \Rightarrow \frac{{x_{}^2}}{3} + \frac{{y_{}^2}}{1} = 1 \Rightarrow \left| {{y_0}} \right| = \frac{{\sqrt {3 – x_0^2} }}{2}\)
Ta có \(AB = 2\left| {{y_0}} \right| = \sqrt {3 – x_0^2} \)
Gọi \(H\)là trung điểm \(AB\)thì \(H\left( {{x_0};0} \right) \Rightarrow OH = {x_0}\)
\({S_{\Delta OAB}} = \frac{1}{2}.OH.AB = \frac{1}{2}.{x_0}.\sqrt {3 – x_0^2} = \frac{1}{2}.\sqrt {x_0^2\left( {3 – x_0^2} \right)} \le \frac{1}{2}.\frac{{x_0^2 + 3 – x_0^2}}{2} = \frac{3}{4}\)
Đẳng thức xảy ra khi\(x_0^2 = 3 – x_0^2 \Rightarrow {x_0} = \frac{{\sqrt 6 }}{2} \Rightarrow {y_0} = \pm \frac{{\sqrt 6 }}{4}\)
Vậy diện tích trồng hoa lớn nhất bằng \(\frac{3}{4}{\rm{ }}{{\rm{m}}^2}.\).
Câu 39: Từ các chữ số \(2,3,4,5,6,7\) lập được bao nhiêu số tự nhiên có \(6\)chữ số khác nhau và tổng ba chữ số đầu nhỏ hơn tổng ba chữ số sau 1 đơn vị?
Phương pháp
Sử dụng công thức tính xác suất
Lời giải
Gọi số cần tìm có dạng \(\overline {abcdef} \) \(\left( {a \ne b \ne c \ne d \ne e \ne f;a,b,c,d,e,f \in \left\{ {2;3;4;5;6;7} \right\}} \right)\).
Theo bài ra, ta có: \(\underbrace {a + b + c}_X + 1 = \underbrace {d + e + f}_Y\).
Và tổng 6 chữa số \(\underbrace {a + b + c}_X + \underbrace {d + e + f}_Y = 27\) suy ra\(\left\{ {\begin{array}{*{20}{l}}{X – Y = – 1}\\{X + Y = 27}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{X = 13}\\{Y = 14}\end{array}} \right.} \right.\).
Khi đó có \(3\) bộ số thỏa mãn là:\((a;b;c) = \left\{ {\left( {3;4;6} \right),\left( {2;5;6} \right),\left( {2;4;7} \right)} \right\}\), ứng với mỗi bộ ba số \(\left( {a,b,c} \right)\) thì tổng ba chữ số còn lại bằng 14 thỏa yêu cầu đề bài.
Vậy có tất cả \(3!.3!.3 = 108\) số.
———- HẾT ———-