Hướng dẫn giải Đề bài Đề thi giữa kì 1 – Đề số 2 – Đề thi đề kiểm tra Toán lớp 10 Chân trời sáng tạo.
Câu hỏi/Đề bài:
I. PHẦN TRẮC NGHIỆM
Câu 1. Kí hiệu nào sau đây viết đúng mệnh đề: “\(\sqrt 2 \) không là số hữu tỉ”
A. \(\sqrt 2 = \mathbb{Q}\) B. \(\sqrt 2 \in \mathbb{Q}\) C. \(\sqrt 2 \subset \mathbb{Q}\) D. \(\sqrt 2 \notin \mathbb{Q}\)
Câu 2. Trong các mệnh đề sau, mệnh đề nào đúng?
A. \(\forall x \in \mathbb{R},{x^2} > 4 \Rightarrow x > – 2\). B. \(\forall x \in \mathbb{R},{x^2} > 4 \Rightarrow x > 2\). C. \(\forall x \in \mathbb{R},x > – 2 \Rightarrow {x^2} > 4\). D. \(\forall x \in \mathbb{R},x > 2 \Rightarrow {x^2} > 4\)
Câu 3. Cho A là tập hợp các số tự nhiên chẵn, \(B = \{ n \in \mathbb{N}|n \le 8\} \) và \(C = \{ n \in \mathbb{N}|2 \le n \le 5\} \).
Tìm tập hợp \(A \cap \left( {B \cup C} \right)\)
A. \(\{ 2;4\} \) B. \(\{ 2\} \). C. \(\{ 4\} \). D. \(\emptyset \).
Câu 4. Cho \(A = ( – 2;5]\) và \(B = (m; + \infty )\). Tìm \(m \in \mathbb{Z}\) để \(A{\rm{\backslash }}B\) chứa đúng 3 số nguyên là:
A. \(0\). B. \(1\). C. \(2\) D. \(3\)
Câu 5. Để chuẩn bị cho các tiết mục văn nghệ, lớp 10B cử ra 12 bạn tham gia tiết mục múa và 7 bạn vào tiết mục hát. Biết rằng có 3 bạn tham gia cả hai tiết mục và 22 bạn không tham gia văn nghệ. Số học sinh lớp 10B là:
A. \(36\). B. \(38\). C. \(40\). D. \(45\).
Câu 6. Miền nghiệm của bất phương trình \(x – 2y \ge 4\) là:
A. 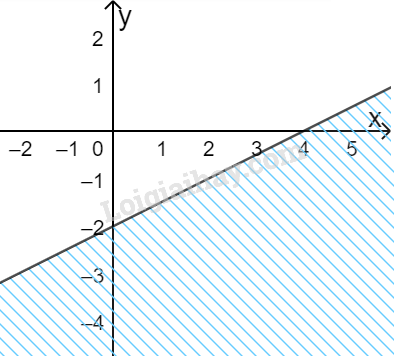 B.
B. 
C. 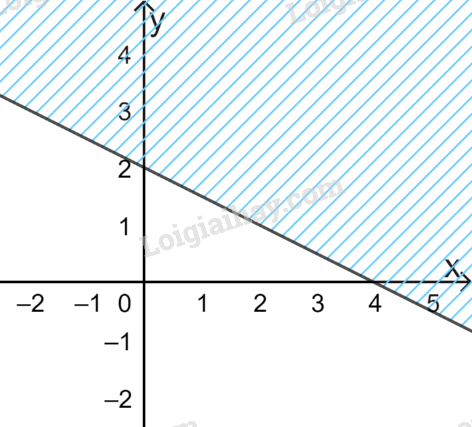 D.
D. 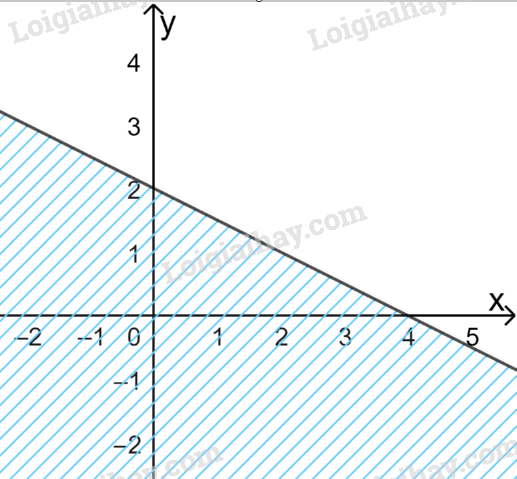
Câu 7. Giá trị lớn nhất của \(F(x;y) = x – 3y\), với điều kiện \(\left\{ \begin{array}{l}x \ge 0\\0 \le y \le 5\\x + y – 2 \ge 0\\3x – y \le 6\end{array} \right.\)
A.\(2\) B. \( – 6\) C.\( – \frac{{34}}{3}\) D. \( – 15\)
Câu 8. Tập xác định của hàm số \(y = \frac{{x – 2}}{{{x^2} – 9}}\)
A. \(\mathbb{R}\). B. \(\mathbb{R}{\rm{\backslash }}\{ 3\} \) C. \(\mathbb{R}{\rm{\backslash }}\{ – 3;3\} \). D. \(\mathbb{R}{\rm{\backslash }}\{ – 3;2;3\} \).
Câu 9. Parabol \((P):y = {x^2} – 6x + 5\) có số điểm chung với trục hoành là
A.\(0\) B. \(1\). C. \(2\). D. \(3\).
Câu 10. Cho hàm số \(f(x)\) xác định trên \(\mathbb{R}\) và có bảng biến thiên như sau:
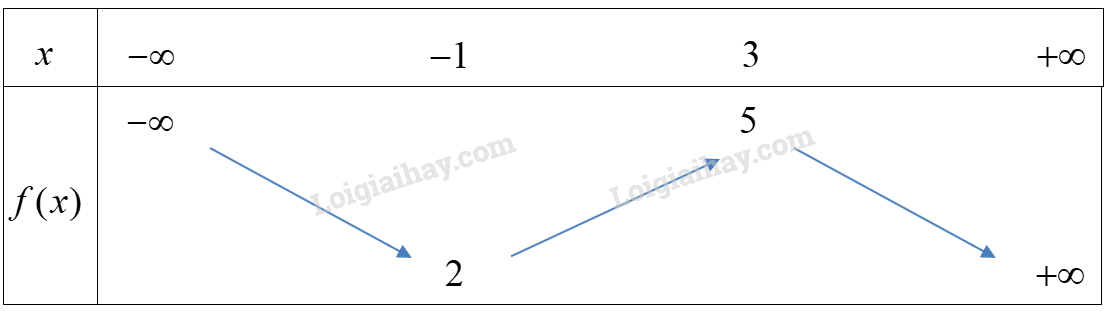
Khẳng định nào sau đây sai?
A. \(f( – 3) > f( – 2)\) B. \(f(2) < f(\sqrt 5 )\) C. \(f(1) < f(0)\) D. \(f(2020) > f(2022)\)
Câu 11. Đường thẳng nào dưới đây song song với đường thẳng \(y = \sqrt 2 x + 1\)
A. \(y = – \sqrt 2 x + 1\) B. \(y = \frac{{\sqrt 2 }}{2}x – 3\) C. \(y = \sqrt 2 x + 5\). D. \(y = \sqrt 2 – 5x\).
Câu 12. Cho hàm số \(f(x) = {x^2} – 4x + 3\). Khẳng định nào sau đây đúng?
A. Hàm số nghịch biến trên \(( – \infty ;2)\), đồng biến trên \((2; + \infty )\).
B. Hàm số nghịch biến trên \((2; + \infty )\), đồng biến trên \(( – \infty ;2)\).
C. Hàm số nghịch biến trên \(\mathbb{R}\).
D. Hàm số đồng biến trên \(\mathbb{R}\).
Câu 13. Điểm \(A(1;2)\) thuộc miền nghiệm của hệ bất phương trình nào dưới đây?
A. \(\left\{ \begin{array}{l}x + 2y > 7\\3x – y < 5\end{array} \right.\) B. \(\left\{ \begin{array}{l}2x – y > 7\\x + y \le 3\end{array} \right.\) C. \(\left\{ \begin{array}{l}3x + 4 \le 10\\4x – y > 3\end{array} \right.\) D. \(\left\{ \begin{array}{l}2x + 5y > 8\\x – 3y \le 4\end{array} \right.\)
Câu 14. Cho hàm số \(f(x) = \left\{ \begin{array}{l}\sqrt {x + 1} – 2\quad (x \ge 1)\\3{x^2} – x + 1\quad (x < 1)\end{array} \right.\). Giá trị của \(2.f( – 3) – 4.f(3)\) là:
A. \(58\) B. \(62\) C. \( – 1\). D. \(1\).
Câu 15. Cho bất phương trình \(2(2x – 3y) – (2x – y + 5) > x – 3y + 1\). Điểm nào dưới đây thuộc miền nghiệm của hệ đã cho?
A. \(O(0;0)\) B. \(A(1;0)\). C. \(B(3; – 2)\). D. \(C(0;2)\)
II. PHẦN TỰ LUẬN
Câu 1. Xác định các tập hợp sau và biểu diễn chúng trên trục số.
a) \(( – \infty ;3) \cap ( – 4; + \infty )\) b) \((1;6] \cup ( – 2;5]\) c) \([ – 3;7){\rm{\backslash }}(1; + \infty )\) d) \(\mathbb{R}{\rm{\backslash }}( – 1;8]\)
Câu 2. Nhà cô Minh có mảnh vườn rộng \(8{m^2}\). Cô dự định trồng cà chua và cải bắp trên toàn bộ mảnh vườn đó. Nếu trồng cà chua thì cần 20 công và thu được 300 nghìn đồng trên mỗi \({m^2}\). Nếu trồng cải bắp thì cần 30 công và thu được 400 nghìn đồng trên mỗi \({m^2}\). Hỏi cần cần trồng mỗi loại cây trên diện tích bao nhiêu để tthu được nhiều tiền nhất mà tổng số công không quá 180?
Câu 3.
a) Xác định parabol (P) biết \((P):y = a{x^2} + bx + c\) đi qua A(0;5) và có đỉnh \(I(3; – 4)\)
b) Xét sự biến thiên và vẽ đồ thị hàm số trên.
Câu 4. Tìm giá trị lớn nhất, nhỏ nhất (nếu có) của hàm số: \(y = 2{x^2} – 4x + 3\) trên đoạn [-1;4].