Lời giải Lời giải Đề thi học kì 1 Toán 10 – Đề số 1 – Đề thi đề kiểm tra Toán lớp 10 Cánh diều.
Câu hỏi/Đề bài:
HƯỚNG DẪN GIẢI CHI TIẾT
I. Phần trắc nghiệm
|
1.D |
2.C |
3.C |
4.B |
5.A |
6.C |
7.B |
8.A |
9.D |
10.C |
|
11.D |
12.C |
13.C |
14.A |
15.B |
16.D |
17.A |
18.A |
19.B |
20.B |
|
21.B |
22.C |
23.D |
24.B |
25.C |
26.A |
27.A |
28.B |
29.B |
30.D |
Câu 1 (NB):
Hướng dẫn:
Liệt kê các phần tử của tập hợp.
Cách giải:
\(S = \left\{ {\left. {q \in \mathbb{Q}} \right|25{q^4} – 9{q^2} = 0} \right\}\).
\(25{q^4} – 9{q^2} = 0 \Leftrightarrow {q^2}\left( {25{q^2} – 9} \right) = 0\)\( \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{{q^2} = 0}\\{25{q^2} – 9 = 0}\end{array}} \right. \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{q = 0}\\{q = \frac{3}{5}}\\{q = \frac{{ – 3}}{5}}\end{array}} \right..\)
Vậy \(S\) có 3 phần tử.
Chọn D.
Câu 2 (NB):
Hướng dẫn:
Quan sát đồ thị, xác định khoảng đồng biến là khoảng ứng với đồ thị đi lên, khoảng nghịch biến là khoảng ứng với đồ thị đi xuống.
Cách giải:
Dựa vào đồ thị hàm số ta thấy hàm số đồng biến trên khoảng \(\left( { – 3;3} \right)\).
Chọn C.
Câu 3 (NB):
Hướng dẫn:
Hàm phân thức xác định khi mẫu thức khác 0.
Cách giải:
ĐKXĐ: \(2x – 2 \ne 0 \Leftrightarrow x \ne 1\).
Vậy TXĐ của hàm số là \(D = \mathbb{R}\backslash \left\{ 1 \right\}\).
Chọn C.
Câu 4 (NB):
Hướng dẫn:
Hàm số bậc hai \(y = a{x^2} + bx + c\) có tọa độ đỉnh \(\left( { – \frac{b}{{2a}};\frac{{ – \Delta }}{{4a}}} \right)\), có bề lõm hướng lên khi a > 0 và hướng xuống khi a < 0.
Cách giải:
Hàm số \(y = {\rm{ \;}} – {x^2} + 2x + 3\) có a = -1, b = 2, c = 3.
Vì a Loại C.
Đồ thị hàm số có tọa độ đỉnh (1;4) => Loại A và D.
Chọn B.
Câu 5 (NB):
Hướng dẫn:
Thay tọa độ các điểm ở các đáp án vào hàm số. Điểm nào thỏa mãn hàm số thì sẽ thuộc đồ thị hàm số.
Cách giải:
Thay tọa độ điểm \({M_1}\left( {2;1} \right)\) vào hàm số: \(1 = \frac{1}{{2 – 1}}\) (đúng) nên \({M_1}\) thuộc đồ thị hàm số.
Chọn A.
Câu 6 (NB):
Hướng dẫn:
– Xác định \(a,{\mkern 1mu} \Delta .\) Xét dấu của \(f\left( x \right)\) theo quy tắc xét dấu tam thức bậc hai.
Cách giải:
Ta có \({x^2} + 12x + 36 = 0\)\( \Leftrightarrow x = {\rm{ \;}} – 6\) và \(a = 1 > 0\).
Nên ta có bảng xét dấu:
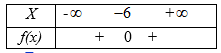
Chọn C.
Câu 7 (NB):
Hướng dẫn:
Sử dụng định nghĩa hai vecto bằng nhau.
Cách giải:
\(\overrightarrow {AB} {\rm{ \;}} = \overrightarrow {CD} {\rm{ \;}} \Rightarrow \left\{ {\begin{array}{*{20}{l}}{AB\parallel CD}\\{AB = CD}\end{array}} \right. \Rightarrow ABDC\) là hình bình hành.
Mặt khác, ABDC là hình bình hành \( \Rightarrow \left\{ {\begin{array}{*{20}{l}}{AB\parallel CD}\\{AB = CD}\end{array}} \right. \Rightarrow \overrightarrow {AB} {\rm{ \;}} = \overrightarrow {CD} \).
Do đó, điều kiện cần và đủ để \(\overrightarrow {AB} {\rm{ \;}} = \overrightarrow {CD} \) là ABDC là hình bình hành.
Chọn B.
Câu 8 (NB):
Hướng dẫn:
Nhóm \(\overrightarrow {AB} ,\overrightarrow {BC} \); \(\overrightarrow {DC} ,\overrightarrow {AD} \), áp dụng quy tắc cộng vectơ.
Cách giải:
Ta có: \(\overrightarrow {AB} {\rm{ \;}} – \overrightarrow {DC} {\rm{ \;}} + \overrightarrow {BC} {\rm{ \;}} – \overrightarrow {AD} {\rm{ \;}} = \left( {\overrightarrow {AB} {\rm{ \;}} + \overrightarrow {BC} } \right) – \left( {\overrightarrow {AD} {\rm{ \;}} + \overrightarrow {DC} } \right) = \overrightarrow {AC} {\rm{ \;}} – \overrightarrow {AC} {\rm{ \;}} = \vec 0\).
Chọn A.
Câu 9 (NB):
Hướng dẫn:
Áp dụng các kiến thức về tam giác đều, đường trung bình trong tam giác.
Cách giải:
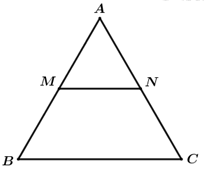
Vì \(\left. {\begin{array}{*{20}{l}}{MA = MB}\\{\overrightarrow {MA} {\rm{\;}} \nearrow {\rm{\;}} \swarrow \overrightarrow {MB} }\end{array}} \right\} \Rightarrow \overrightarrow {MA} {\rm{\;}} = {\rm{\;}} – \overrightarrow {MB} \) nên đáp án A sai.
Vì \(\overrightarrow {AB} \) và \(\overrightarrow {AC} \) không cùng phương nên đáp án B sai.
Vì \(\left. {\begin{array}{*{20}{l}}{MN = \frac{1}{2}BC}\\{\overrightarrow {MN} {\rm{\;}} \nearrow {\rm{\;}} \nearrow \overrightarrow {BC} }\end{array}} \right\} \Rightarrow \overrightarrow {MA} {\rm{\;}} = \frac{1}{2}\overrightarrow {BC} \) nên đáp án C sai.
Vì MN là đường trung bình của \(\Delta ABC\) nên \(\left| {\overrightarrow {BC} } \right| = 2\left| {\overrightarrow {MN} } \right|\).
Chọn D.
Câu 10 (TH):
Hướng dẫn:
Thay tọa độ điểm A, B vào hàm số.
Giải hệ phương trình tìm a, c và xác định hàm số bậc hai.
Cách giải:
Vì A, B thuộc đồ thị hàm số nên ta có hệ phương trình: \(\left\{ {\begin{array}{*{20}{l}}{ – 2 = a – 1 + c}\\{3 = 4a – 2 + c}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{a + c = {\rm{ \;}} – 1}\\{4a + c = 5}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{a = 2}\\{b = {\rm{ \;}} – 3}\end{array}} \right.\)
Vậy hàm số bậc hai là \(y = 2{x^2} – x – 3\).
Chọn C.
Câu 11 (TH):
Hướng dẫn:
Khi a > 0, hàm số \(y = a{x^2} + bx + c\) có GTNN bằng \( – \frac{\Delta }{{4a}}\) tại \(x = {\rm{ \;}} – \frac{b}{{2a}}\).
Cách giải:
Hàm số \(y = {x^2} – 4x + 5\) có a = 1, b = -4, c = 5.
\( \Rightarrow \Delta {\rm{ \;}} = {\left( { – 4} \right)^2} – 4.1.5 = {\rm{ \;}} – 4\).
Vậy hàm số có GTNN bằng \( – \frac{\Delta }{{4a}} = {\rm{ \;}} – \frac{{ – 4}}{{4.1}} = 1\) tại \(x = {\rm{ \;}} – \frac{b}{{2a}} = {\rm{ \;}} – \frac{{ – 4}}{{2.1}} = 2\).
Chọn D.
Câu 12 (TH):
Hướng dẫn:
Dùng quy tắc xét dấu của tam thức bậc hai. Hoặc biến đổi về hằng đẳng thức rồi giải bất phương trình.
Cách giải:
\(f\left( x \right) = {x^2} + 4x + m – 5 = \left( {{x^2} + 4x + 4} \right) + m – 9 = {\left( {x + 2} \right)^2} + \left( {m – 9} \right)\).
Ta có: \({\left( {x + 2} \right)^2} \ge 0,\forall x\).
Để \(f\left( x \right) > 0,\forall x\) thì \(m – 9 > 0 \Leftrightarrow m > 9\).
Chọn C.
Câu 13 (TH):
Hướng dẫn:
Hàm số xác định khi \(\frac{2}{{{x^2} + 5x – 6}} \ge 0\) và \({x^2} + 5x – 6 \ne 0.\)
Xét dấu các tam thức bậc 2 và kết luận nghiệm.
Cách giải:
Hàm số xác định khi \(\frac{2}{{{x^2} + 5x – 6}} \ge 0\) và \({x^2} + 5x – 6 \ne 0.\)
\( \Leftrightarrow {x^2} + 5x – 6 > 0.\)
Ta có \(a = 1 > 0\), \({x^2} + 5x – 6\) có hai nghiệm là \(x = 1;x = {\rm{ \;}} – 6\)
Vậy \({x^2} + 5x – 6 > 0 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{x 1}\end{array}} \right..\)
Chọn C.
Câu 14 (TH):
Hướng dẫn:
\(\sqrt {f\left( x \right)} {\rm{\;}} = a{\mkern 1mu} {\mkern 1mu} \left( {a > 0} \right) \Leftrightarrow f\left( x \right) = {a^2}\)
Cách giải:
\(\begin{array}{*{20}{l}}{\sqrt {{x^2} – 4x – 1} {\rm{\;}} = 2}\\{ \Leftrightarrow {x^2} – 4x – 1 = 4}\\{ \Leftrightarrow {x^2} – 4x – 5 = 0}\\{ \Leftrightarrow \left( {x – 5} \right)\left( {x + 1} \right) = 0}\\{ \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{x – 5 = 0}\\{x + 1 = 0}\end{array}} \right. \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{x = 5}\\{x = {\rm{\;}} – 1}\end{array}} \right.}\end{array}\)
Vậy \(S = \left\{ {5; – 1} \right\}\).
Chọn A.
Câu 15 (TH):
Hướng dẫn:
Gọi M là trung điểm BC, tính độ dài AM.
Sử dụng tính chất của trọng tâm G \(\left( {AG = \frac{2}{3}AM} \right)\) để tính AG.
Cách giải:
Gọi M là trung điểm của BC.
Tam giác ABC đều cạnh 1 suy ra \(AM = \frac{{\sqrt 3 }}{2}.\)
Ta có: \(\left| {\overrightarrow {AG} } \right| = AG = \frac{2}{3}AM = \frac{2}{3} \cdot \frac{{\sqrt 3 }}{2} = \frac{{\sqrt 3 }}{3}\).
Chọn B.
Câu 16 (TH):
Hướng dẫn:
Liệt kê các vecto có điểm cuối là A từ các điểm A, B, C, D, E.
Cách giải:
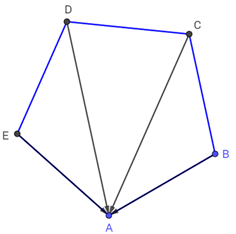
Ta có 4 vectơ thỏa đề bài: \(\overrightarrow {BA} ,{\mkern 1mu} \overrightarrow {CA} ,\overrightarrow {DA} ,{\mkern 1mu} \overrightarrow {EA} .\)
Chọn D.
Câu 17 (TH):
Hướng dẫn:
+ Xác định \(\vec c\) và \(\left| {\vec c} \right|\). Tính \(\vec a.\vec c\).
+ Áp dụng công thức \(\cos \left( {\vec a,{\mkern 1mu} {\mkern 1mu} \vec c} \right) = \frac{{\vec a{\mkern 1mu} .{\mkern 1mu} {\mkern 1mu} \vec c}}{{\left| {\vec a} \right|{\mkern 1mu} .{\mkern 1mu} {\mkern 1mu} \left| {\vec c} \right|}}\) để tìm \(\left( {\vec a,{\mkern 1mu} {\mkern 1mu} \vec c} \right)\).
Cách giải:
\(\left| {\vec a} \right| = 2\), \(\left| {\vec b} \right| = 1\) và \(\left( {\vec a,{\mkern 1mu} {\mkern 1mu} \vec b} \right) = {60^0}\).
Ta có:
\({\vec c^2} = {\left( {\vec a – \vec b} \right)^2}\)\( = {\vec a^2} + {\vec b^2} – 2\vec a\vec b\)\( = {\vec a^2} + {\vec b^2} – 2.\left| {\vec a} \right|.\left| {\vec b} \right|.\cos \left( {\vec a,{\mkern 1mu} {\mkern 1mu} \vec b} \right)\)\( = {2^2} + {1^2} – 2.2.1.cos{60^0}\) \( = 3\)
\( \Rightarrow \left| {\vec c} \right| = \sqrt 3 \)
\(\vec a.\vec c = \vec a.\left( {\vec a – \vec b} \right)\)\( = {\vec a^2} – \vec a.\vec b\)\( = {\vec a^2} – \left| {\vec a} \right|.\left| {\vec b} \right|.\cos \left( {\vec a,{\mkern 1mu} {\mkern 1mu} \vec b} \right)\)\( = {2^2} – 2.1.\cos {60^0} = 3\)
Mà \(\cos \left( {\vec a,{\mkern 1mu} {\mkern 1mu} \vec c} \right) = \frac{{\vec a.\vec c}}{{\left| {\vec a} \right|.\left| {\vec c} \right|}}\)\( = \frac{3}{{2.\sqrt 3 }} = \frac{{\sqrt 3 }}{2}\)
Vậy \(\cos \left( {\vec a,{\mkern 1mu} {\mkern 1mu} \vec c} \right)\)\( = \frac{{\sqrt 3 }}{2}\) \( \Rightarrow \angle \left( {\vec a,{\mkern 1mu} {\mkern 1mu} \vec c} \right) = {30^0}\)
Chọn A.
Câu 18 (TH):
Hướng dẫn:
Dùng tính chất vectơ và độ dài vectơ
Cách giải:
\(\begin{array}{*{20}{l}}{AC = \sqrt {B{C^2} – A{B^2}} {\rm{ \;}} = 4}\\{ \Rightarrow \left| {\overrightarrow {AB} {\rm{ \;}} – \overrightarrow {CB} } \right| = \left| {\overrightarrow {AB} {\rm{ \;}} + \overrightarrow {BC} } \right| = \left| {\overrightarrow {AC} } \right| = 4}\end{array}\)
Chọn A.
Câu 19 (TH):
Hướng dẫn:
Áp dụng định nghĩa tích của vecto với một số, quy tắc cộng vecto, quy tắc hình bình hành để phân tích vecto theo các vecto khác.
Cách giải:
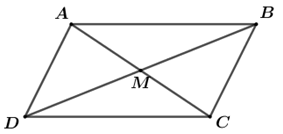
Vì ABCD là hình bình hành nên \(DB = 2DM\).
\(\overrightarrow {DM} {\rm{\;}} = \frac{1}{2}\overrightarrow {DB} {\rm{\;}} = \frac{1}{2}\left( {\overrightarrow {DA} {\rm{\;}} + \overrightarrow {DC} } \right)\)\( = \frac{1}{2}\left( {\overrightarrow {CB} {\rm{\;}} – \overrightarrow {CD} } \right) = – \frac{1}{2}\overrightarrow {BC} {\rm{\;}} – \frac{1}{2}\overrightarrow {CD} \)
Chọn B.
Câu 20 (TH):
Hướng dẫn:
Sử dụng công thức \(\vec a.\vec b{\rm{\;}} = \left| {\vec a} \right|.\left| {\vec b} \right|.\cos \left( {\vec a;\vec b} \right)\).
Cách giải:
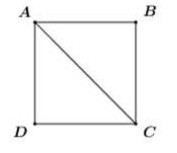
Vì ABCD là hình vuông cạnh a nên AB = BC = a và AC là phân giác của góc BAD.
\( \Rightarrow \angle BAC = {45^0} = \left( {\overrightarrow {AB} ;\overrightarrow {AC} } \right)\).
Áp dụng định lí Pytago trong tam giác vuông ABC ta có:
\(\begin{array}{*{20}{l}}{A{C^2} = A{B^2} + B{C^2}}\\{A{C^2} = {a^2} + {a^2} = 2{a^2}}\\{ \Rightarrow AC = a\sqrt 2 }\end{array}\)
Vậy \(\overrightarrow {AB} .\overrightarrow {AC} {\rm{\;}} = AB.AC.\cos \left( {\overrightarrow {AB} ;\overrightarrow {AC} } \right)\) \( = a.a\sqrt 2 .\cos {45^0}\)\( = {a^2}\sqrt 2 .\frac{{\sqrt 2 }}{2}\) \( = {a^2}\).
Chọn B.
Câu 21 (VD):
Hướng dẫn:
Lập hàm số bậc hai biểu thị khối lượng cá theo hoạch sau mỗi vụ theo ẩn x.
Tìm GTLN của hàm số.
Cách giải:
Khối lượng cá thu hoạch sau mỗi vụ là: \(f\left( x \right) = x\left( {480 – 20x} \right) = {\rm{ \;}} – 20{x^2} + 480x{\mkern 1mu} {\mkern 1mu} \left( {gam} \right)\).
f(x) là hàm số bậc hai có a = -20, b = 480, c = 0 \( \Rightarrow \Delta {\rm{ \;}} = {480^2}\).
=> Giá trị lớn nhất của hàm số bằng \(\frac{{ – \Delta }}{{4a}} = \frac{{ – {{480}^2}}}{{4.\left( { – 20} \right)}} = {\rm{ \;}} – 2880\) đạt được tại \(x = \frac{{ – b}}{{2a}} = \frac{{ – 480}}{{2.\left( { – 20} \right)}} = 12\).
Vậy để sau mỗi vụ thu hoạch được nhiều cá nhất phải thả 12 con cá trên một đơn vị diện tích của mặt hồ.
Chọn B.
Câu 22 (VD):
Hướng dẫn:
Xét các trường hợp: \(\Delta ‘ 0\)
Cách giải:
Đặt \(f\left( x \right) = {\rm{\;}} – 2{x^2} + 2\left( {m – 2} \right)x + m – 2\).
\(\Delta ‘ = {\left( {m – 2} \right)^2} + 2\left( {m – 2} \right) = {m^2} – 2m\)
+) \(\left\{ {\begin{array}{*{20}{l}}{a = {\rm{\;}} – 2 < 0}\\{\Delta ' < 0}\end{array}} \right.\)\( \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{a = {\rm{\;}} – 2 < 0}\\{{m^2} – 2m < 0}\end{array}} \right.\)\( \Leftrightarrow 0 < m < 2\)
\( \Rightarrow f\left( x \right) < 0,{\mkern 1mu} {\mkern 1mu} \forall x \in \mathbb{R}\)
Vậy bất phương trình \( – 2{x^2} + 2\left( {m – 2} \right)x + m – 2 \ge 0\) vô nghiệm.
\( \Rightarrow \) Loại
+) \(\Delta ‘ = 0 \Leftrightarrow {m^2} – 2m = 0\)\( \Leftrightarrow m\left( {m – 2} \right) = 0\)\( \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{m = 0}\\{m = 2}\end{array}} \right.\)
\( \Rightarrow f\left( x \right) = 0\)\( \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{ – 2{x^2} – 4x – 2 = 0}\\{ – 2{x^2} = 0}\end{array}} \right.\)\( \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{x = {\rm{\;}} – 1}\\{x = 0}\end{array}} \right.\) (thỏa mãn)
Vậy bất phương trình \( – 2{x^2} + 2\left( {m – 2} \right)x + m – 2 \ge 0\) có nghiệm \(\left[ {\begin{array}{*{20}{l}}{x = {\rm{\;}} – 1}\\{x = 0}\end{array}} \right.\).
\( \Rightarrow \) Nhận \(m = 0;{\mkern 1mu} {\mkern 1mu} m = 2\).
+) \(\Delta ‘ > 0\)\( \Leftrightarrow {m^2} – 2m > 0\)\( \Leftrightarrow m\left( {m – 2} \right) > 0\)\( \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{m 2}\end{array}} \right.\)
\( \Rightarrow f\left( x \right) = 0\) có hai nghiệm phân biệt \({x_1},{\mkern 1mu} {\mkern 1mu} {x_2}\) (giả sử \({x_1} < {x_2}\))
Bảng xét dấu:

Dựa vào bảng xét dấu, ta có: \(f\left( x \right) \ge 0 \Leftrightarrow {x_1} \le x \le {x_2}\)
\( \Rightarrow \) Nhận \(\left[ {\begin{array}{*{20}{l}}{m 2}\end{array}} \right.\)
Kết hợp các trường hợp, ta được \(m \in \left( { – \infty ;{\mkern 1mu} {\mkern 1mu} 0} \right] \cup \left[ {2;{\mkern 1mu} {\mkern 1mu} + \infty } \right)\).
Vậy \(m \in \left( { – \infty ;{\mkern 1mu} 0} \right] \cup \left[ {2;{\mkern 1mu} + \infty } \right)\).
Chọn C.
Câu 23 (VD):
Hướng dẫn:
– Giải phương trình chứa căn \(\sqrt A {\rm{\;}} = B \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{B \ge 0}\\{A = {B^2}}\end{array}} \right.\).
– Sử dụng định lí Vi-ét.
Cách giải:
Ta có:
\(\begin{array}{*{20}{l}}{\sqrt {{x^2} + mx + 2} {\rm{\;}} = 2x + 1}\\{ \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{x \ge {\rm{\;}} – \frac{1}{2}}\\{{x^2} + mx + 2 = 4{x^2} + 4x + 1}\end{array}} \right.}\\{ \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{x \ge {\rm{\;}} – \frac{1}{2}}\\{3{x^2} – \left( {m – 4} \right)x – 1 = 0{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} \left( * \right)}\end{array}} \right.}\end{array}\)
Để phương trình ban đầu có 2 nghiệm phân biệt thì phương trình (*) phải có 2 nghiệm phân biệt \({x_1} > {x_2} \ge {\rm{\;}} – \frac{1}{2}\).
\( \Rightarrow \left\{ \begin{array}{l}\Delta > 0\\{x_1} + {x_2} > – 1\\\left( {{x_1} + \frac{1}{2}} \right)\left( {{x_2} + \frac{1}{2}} \right) \ge 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{\left( {m – 4} \right)^2} + 12 > 0\,\,(luon\,\,\,dung)\\\frac{{m – 4}}{3} > – 1\\\frac{{ – 1}}{3} + \frac{1}{2}.\frac{{m – 4}}{3} + \frac{1}{4} \ge 0\end{array} \right.\)
\( \Leftrightarrow \left\{ \begin{array}{l}m – 4 > – 3\\\frac{{m – 4}}{6} \ge \frac{1}{{12}}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}m > 1\\m – 4 \ge \frac{1}{2}\end{array} \right. \Leftrightarrow m \ge \frac{9}{2}.\)
Vậy \(m \ge \frac{9}{2}\).
Chọn D.
Câu 24 (VD):
Hướng dẫn:
– Mô hình hoá bài toán.
– Tính BC dựa vào định lí côsin trong tam giác ABC.
– Tính thời gian chèo thuyền bằng công thức \(t = \frac{s}{v}\). Trong đó: t là thời gian; s là quãng đường; v là vận tốc.
Cách giải:
Áp dụng định lí Cô sin cho tam giác ABC ta có:
\(B{C^2} = A{B^2} + A{C^2} – 2AB.AC.\cos A\) =0,28 km.
Vậy thời gian du khách chèo thuyền từ \(C\) đến \(B\) là: \(t = \frac{{BC}}{v}\)\( = \frac{{0,28}}{4}\)\( = 0,07\) giờ \( = 4,2\) phút.
Chọn B.
Câu 25 (VD):
Hướng dẫn:
– Vẽ hình.
– Xét xem \(\overrightarrow {AM} \)có bằng \(\overrightarrow {NC} \) không bằng cách xét ANCM có là hình bình hành không.
– Xét xem DP có bằng QB không.
Cách giải:
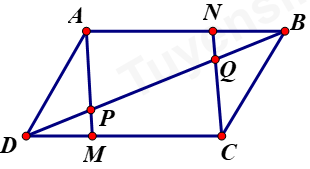
Ta có \(DM = BN \Rightarrow AN = MC\), mặt khác AN song song với MC do đó tứ giác ANCM là hình bình hành
Suy ra \(\overrightarrow {AM} {\rm{ \;}} = \overrightarrow {NC} \).
Xét tam giác \(\Delta DMP\) và \(\Delta BNQ\) ta có \(DM = NB\) (giả thiết), \(\widehat {PDM} = \widehat {QBN}\) (so le trong)
Mặt khác \(\widehat {DPM} = \widehat {APB}\) (đối đỉnh) và \(\widehat {APQ} = \widehat {NQB}\) (hai góc đồng vị) suy ra \(\widehat {DPM} = \widehat {NQB}\).
Suy ra: \(\widehat {DMP} = \widehat {BNQ}\).
Do đó \(\Delta DMP = \Delta BNQ\) (c.g.c) suy ra \(DP = QB\).
Dễ thấy \(\overrightarrow {DP} ,{\mkern 1mu} {\mkern 1mu} \overrightarrow {QB} \) cùng hướng vì vậy \(\overrightarrow {DP} {\rm{ \;}} = \overrightarrow {QB} \).
Chọn C.
Câu 26 (VD):
Hướng dẫn:
Dùng tính chất vectơ và độ dài vectơ
Cách giải:
\(\left| {\overrightarrow {MA} {\rm{ \;}} – \overrightarrow {MB} } \right| = \left| {\overrightarrow {MC} } \right| \Rightarrow \left| {\overrightarrow {BA} } \right| = \left| {\overrightarrow {MC} } \right|\) => M nằm trên 1 đường tròn tâm C bán kính AB
Chọn A.
Câu 27 (VD):
Hướng dẫn:
Thu gọn các biểu thức vecto ở hai vế.
Tìm quỹ tích điểm \(M\) dựa vào đẳng thức vecto vừa thu gọn.
Cách giải:
Theo bài ra, ta có: \({\mkern 1mu} x\overrightarrow {MA} {\rm{\;}} + y\overrightarrow {MB} {\rm{\;}} + z\overrightarrow {MC} {\rm{\;}} = \vec 0\)
\( \Leftrightarrow x\overrightarrow {MA} {\rm{\;}} + y\left( {\overrightarrow {MA} {\rm{\;}} + \overrightarrow {AB} } \right) + z\left( {\overrightarrow {MA} {\rm{ \;}} + \overrightarrow {AC} } \right) = \vec 0\)
\( \Leftrightarrow x\overrightarrow {MA} {\rm{\;}} + y\overrightarrow {MA} {\rm{\;}} + y\overrightarrow {AB} {\rm{\;}} + z\overrightarrow {MA} {\rm{\;}} + z\overrightarrow {AC} {\rm{\;}} = \vec 0\)
\( \Leftrightarrow \left( {x\overrightarrow {MA} {\rm{\;}} + y\overrightarrow {MA} {\rm{\;}} + z\overrightarrow {MA} } \right) + \left( {y\overrightarrow {AB} {\rm{\;}} + z\overrightarrow {AC} } \right) = \vec 0\)
\( \Leftrightarrow \left( {x + y + z} \right)\overrightarrow {MA} {\rm{\;}} + \left( {y\overrightarrow {AB} {\rm{\;}} + z\overrightarrow {AC} } \right) = \vec 0\)
\( \Leftrightarrow \left( {x + y + z} \right)\overrightarrow {MA} {\rm{\;}} = {\rm{\;}} – y\overrightarrow {AB} {\rm{\;}} – z\overrightarrow {AC} \)
Đặt \( – y\overrightarrow {AB} {\rm{\;}} – z\overrightarrow {AC} {\rm{\;}} = \vec u\). Khi đó, ta có: \(\left( {x + y + z} \right)\overrightarrow {MA} {\rm{\;}} = \vec u\)
Do đó, nếu \(x + y + z \ne 0\) thì tồn tại duy nhất điểm \(M\) thỏa mãn đẳng thức trên.
Chọn A.
Câu 28 (VD):
Hướng dẫn:
Từ \(\overrightarrow {AB} {\rm{\;}} = \overrightarrow {OB} {\rm{\;}} – \overrightarrow {OA} \) chứng minh được \(OA = OB\). Từ đó, rút ra kết luận.
Cách giải:
Ta có:
\(\left( {\overrightarrow {OA} {\rm{\;}} + \overrightarrow {OB} } \right).\overrightarrow {AB} {\rm{\;}} = 0\)
\( \Leftrightarrow \left( {\overrightarrow {OB} {\rm{\;}} + \overrightarrow {OA} } \right).\left( {\overrightarrow {OB} {\rm{\;}} – \overrightarrow {OA} } \right) = 0\)
\( \Leftrightarrow O{B^2} – O{A^2} = 0\)
\( \Leftrightarrow OA = OB\)
\( \Rightarrow \Delta AOB\) cân tại \(O\).
Vậy điều kiện cần và đủ để \(\left( {\overrightarrow {OA} {\rm{\;}} + \overrightarrow {OB} } \right).\overrightarrow {AB} {\rm{\;}} = 0\) là \(\Delta AOB\) cân tại \(O\).
Chọn B.
Câu 29 (VDC):
Cách giải:
Xét tam thức: \(f\left( x \right) = {x^2} + mx + {m^2} + 6m\)
Để \(f\left( x \right) < 0\forall x \in \left( {1;2} \right) \Rightarrow {x_1} < 1 < 2 < {x_2}\) trong đó \({x_1},{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {x_2}\) là hai nghiệm của tam thức.
Áp dụng định lí Vi-ét ta có: \(\left\{ {\begin{array}{*{20}{l}}{{x_1} + {x_2} = {\rm{\;}} – m}\\{{x_1}{x_2} = {m^2} + 6m}\end{array}} \right.\)
Từ đây ta có:
\(\left\{ \begin{array}{l}\Delta > 0\\{x_1} < 1 < {x_2}\\{x_1} < 2 0\\\left( {{x_1} – 1} \right)\left( {{x_2} – 1} \right) < 0\\\left( {{x_1} – 2} \right)\left( {{x_2} – 2} \right) < 0\end{array} \right.\)
\( \Leftrightarrow \left\{ \begin{array}{l}{m^2} – 4\left( {{m^2} + 6m} \right) > 0\\{x_1}{x_2} – \left( {{x_1} + {x_2}} \right) + 1 < 0\\{x_1}{x_2} – 2\left( {{x_1} + {x_2}} \right) + 4 < 0\end{array} \right.\)
\( \Leftrightarrow \left\{ \begin{array}{l} – 3{m^2} – 24m > 0\\{m^2} + 6m + m + 1 > 0\\{m^2} + 6m + 2m + 4 < 0\end{array} \right.\)
\( \Leftrightarrow \left\{ \begin{array}{l} – 8 < m < 0\\\frac{{ – 7 – 3\sqrt 5 }}{2} < m < \frac{{ – 7 + 3\sqrt 5 }}{2}\\ – 4 – 2\sqrt 3 < m < – 4 + 2\sqrt 3 \end{array} \right.\)
\( \Leftrightarrow \frac{{ – 7 – 3\sqrt 5 }}{2} < m < – 4 + 2\sqrt 3 \)
Mà \(m\) nguyên nên \(m = {\rm{\;}} – 6\).
Chọn B.
Câu 30 (VDC):
Hướng dẫn:
+) Từ hai hình chiếu của \(C\) lên AB,AD, ta biến đổi các các đẳng thức theo đề bài để đưa ra đáp án đúng.
Cách giải:
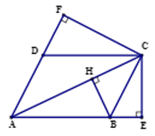
Vì E,F lần lượt là hình chiếu của \(C\) lên AB,AD nên ta có:
\(\begin{array}{*{20}{l}}{\overrightarrow {AB} .\overrightarrow {AE} {\rm{\;}} = \overrightarrow {AC} .\overrightarrow {AB} }\\{\overrightarrow {AD} .\overrightarrow {AF} {\rm{\;}} = \overrightarrow {AC} .\overrightarrow {AD} }\end{array}\)
Suy ra \(\overrightarrow {AB} .\overrightarrow {AE} {\rm{\;}} + \overrightarrow {AD} .\overrightarrow {AF} {\rm{\;}} = \overrightarrow {AC} .\overrightarrow {AB + } \overrightarrow {AC} .\overrightarrow {AD} {\rm{\;}} = {\overrightarrow {AC} ^2}\left( * \right)\)
Do AC là đường chéo lớn nên \(\angle ABC \ge {90^o}\) và \(B\) nằm giữa hai điểm \(A\) và E. Suy ra \(\overrightarrow {AB} .\overrightarrow {AE} {\rm{\;}} = AB.AE\)
Tương tự ta có \(D\) nằm giữa hai điểm \(A\) và F. Suy ra \(\overrightarrow {AD} .\overrightarrow {AF} {\rm{\;}} = AD.AF\)
Vậy \(\left( * \right)\) trở thành: \(AB.AE + AD.AF = A{C^2}\)
Chọn D.
II. Phần tự luận (4 điểm)
Câu 1 (TH):
Hướng dẫn:
a) Nhóm \(\overrightarrow {IB} \) và \(\overrightarrow {IC} \).
b) Tính IA, IB. Tính \(\cos \angle BIA\)theo hệ quả định lí cosin trong tam giác BIA.
c) Sử dụng: \(\overrightarrow {MB} {\rm{ \;}} = \overrightarrow {MI} {\rm{ \;}} + \overrightarrow {IB} \), \(\overrightarrow {MC} {\rm{ \;}} = \overrightarrow {MI} {\rm{ \;}} + \overrightarrow {IC} \),\(\overrightarrow {MA} {\rm{ \;}} = \overrightarrow {MI} {\rm{ \;}} + \overrightarrow {IA} \) thay vào điều điện đề bài cho để tìm MI.
Cách giải:
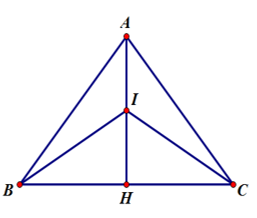
a) Chứng minh \(2\overrightarrow {IA} {\rm{ \;}} + \overrightarrow {IB} {\rm{ \;}} + \overrightarrow {IC} {\rm{ \;}} = \vec 0\).
\(VT = \left( {\overrightarrow {IB} {\rm{ \;}} + \overrightarrow {IC} } \right) + 2\overrightarrow {IA} {\rm{ \;}} = 2\overrightarrow {IH} {\rm{ \;}} + 2\overrightarrow {IA} {\rm{ \;}} = 2\left( {\overrightarrow {IH} {\rm{ \;}} + \overrightarrow {IA} } \right) = 2.\vec 0{\rm{ \;}} = \vec 0{\rm{ \;}} = VP\) (Đpcm).
b) Tính \(\cos \angle BIA\).
Ta có \(IH = IA = \frac{1}{2}AH = \frac{{a\sqrt 3 }}{4}\); \(IB = IC = \sqrt {B{H^2} + I{H^2}} {\rm{ \;}} = \sqrt {\frac{{{a^2}}}{4} + \frac{{3{a^2}}}{{16}}} {\rm{ \;}} = \frac{{a\sqrt 7 }}{4}\).
\(\cos \widehat {BIA} = \frac{{I{B^2} + I{A^2} – B{A^2}}}{{2IB.IA}} = \frac{{\frac{{7{a^2}}}{{16}} + \frac{{3{a^2}}}{{16}} – {a^2}}}{{2\frac{{a\sqrt 7 }}{4}\frac{{a\sqrt 3 }}{4}}} = {\rm{ \;}} – \frac{3}{{\sqrt {21} }}\).
c)
\(\begin{array}{*{20}{l}}{M{B^2} + M{C^2} + 2M{A^2} = {{\left( {\overrightarrow {MI} {\rm{ \;}} + \overrightarrow {IB} } \right)}^2} + {{\left( {\overrightarrow {MI} {\rm{ \;}} + \overrightarrow {IC} } \right)}^2} + 2{{\left( {\overrightarrow {MI} {\rm{ \;}} + \overrightarrow {IA} } \right)}^2}}\\{ = 4M{I^2} + 2I{A^2} + I{B^2} + I{C^2} = 4M{I^2} + \frac{{20{a^2}}}{{16}}}\end{array}\)
Suy ra \(MI = \frac{a}{2}\). Vậy điểm tập hợp các điểm \(M\) là đường tròn tâm \(I\) bán kính \(R = \frac{a}{2}\).
Câu 2 (VD):
Hướng dẫn:
Chọn hệ trục toạ độ như hình vẽ.
Giả sử Parabol có phương trình \(\left( P \right):{\mkern 1mu} y = a{x^2} + bx + c\).
Tìm (P) biết P đi qua các điểm \(O\left( {0;0} \right),{\mkern 1mu} {\mkern 1mu} M\left( {10;{\mkern 1mu} 43} \right),{\mkern 1mu} {\mkern 1mu} N\left( {162;0} \right)\).
Chiều cao của cổng là tung độ đỉnh của parabol.
Cách giải:
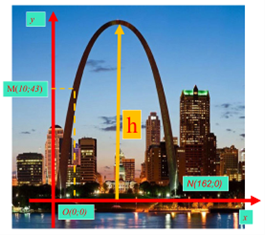
Chọn hệ trục tọa độ Oxy sao cho một chân cổng đi qua gốc \(O\) như hình vẽ trên, chân kia là điểm \(N\left( {162;{\mkern 1mu} 0} \right).\)Giả sử Parabol có phương trình \(\left( P \right):{\mkern 1mu} y = a{x^2} + bx + c\).
Khi đó Parabol \(\left( P \right)\) đi qua các điểm \(O\left( {0;0} \right),{\mkern 1mu} {\mkern 1mu} M\left( {10;{\mkern 1mu} 43} \right),{\mkern 1mu} {\mkern 1mu} N\left( {162;0} \right)\) nên ta có
\(\left\{ {\begin{array}{*{20}{l}}{c = 0}\\{26244a + 162b + c = 0}\\{100a + 10b + c = 43}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{a = {\rm{ \;}} – \frac{{43}}{{1520}}}\\{b = \frac{{3483}}{{\begin{array}{*{20}{l}}{760}\\{c = 0}\end{array}}}}\end{array}} \right.\).
Do đó \(\left( P \right):y = {\rm{ \;}} – \frac{{43}}{{1520}}{x^2} + \frac{{3483}}{{760}}x\).
Khi đó chiều cao của cổng là \(h = y\left( {81} \right) = {\rm{ \;}} – \frac{\Delta }{{4a}} = \frac{{282123}}{{1520}} \approx 185,6\left( m \right).\)
Câu 3 (VD):
Hướng dẫn:
Xét các trường hợp: \(a = 0\), \(a \ne 0\): Phương trình bậc hai có nghiệm khi và chỉ khi \(\Delta \; \ge 0\).
Cách giải:
Xét phương trình: \(\left( {m – 5} \right){x^2} – 4mx + m – 2 = 0\left( 1 \right)\)
Trường hợp 1: \(m – 5 = 0 \Leftrightarrow m = 5\)
Phương trình \(\left( 1 \right)\) trở thành: \( – 20x + 3 = 0 \Leftrightarrow x = \frac{3}{{20}}\)
\( \Rightarrow \) Với \(m = 5\) phương trình \(\left( 1 \right)\) có nghiệm duy nhất \(x = \frac{3}{{20}}\).
Trường hợp 2: \(m – 5 \ne 0 \Leftrightarrow m \ne 5\)
Phương trình \left( 1 \right) có nghiệm khi và chỉ khi:
\(\Delta ‘ \ge 0 \Leftrightarrow {\left( { – 2m} \right)^2} – \left( {m – 5} \right)\left( {m – 2} \right) \ge 0\)\( \Leftrightarrow 4{m^2} – \left( {{m^2} – 7m + 10} \right) \ge 0\)\( \Leftrightarrow 3{m^2} – 7m – 10 \ge 0\)\( \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{m \ge 1}\\{m \le \; – \frac{{10}}{3}}\end{array}} \right.\)
Kết hợp với điều kiện \(m \ne 5\) ta có: \(m \in \left( { – \infty ;{\rm{\;}}\frac{{10}}{3}} \right] \cup \left[ {1; + \infty } \right)\backslash \left\{ 5 \right\}\)
Kết hợp cả hai trường hợp ta có: \(m \in \left( { – \infty ; – \frac{{10}}{3}} \right] \cup \left[ {1; + \infty } \right)\) hay \(\left[ {\begin{array}{*{20}{l}}{m \le \; – \frac{{10}}{3}}\\{m \ge 1}\end{array}} \right.\).