Giải chi tiết Giải đề 8 Tổng hợp 10 đề thi học kì 1 Toán 10 Cánh diều – Đề thi đề kiểm tra Toán lớp 10 Cánh diều.
Câu hỏi/Đề bài:
HƯỚNG DẪN GIẢI CHI TIẾT
Phần 1: Trắc nghiệm (25 câu – 5 điểm)
|
1.C |
2.D |
3.A |
4.A |
5.C |
6.A |
7.B |
8.B |
9.C |
10.D |
|
11.D |
12.C |
13.D |
14.B |
15.C |
16.A |
17.C |
18.D |
19.B |
20.B |
|
21.A |
22.D |
23.A |
24.B |
25.A |
|
|
|
|
|
Câu 1 (NB):
Hướng dẫn:
Mệnh đề là những khẳng định có tính đúng hoặc sai.
Cách giải:
Câu a) là câu cảm thán không phải là mệnh đề.
Các câu b, c, d là mệnh đề => Có 3 mệnh đề.
Chọn C.
Câu 2 (TH):
Hướng dẫn:
Gọi M là trung điểm BC.
Sử dụng tính chất trung điểm.
Cách giải:
Gọi \(M\) là trung điểm BC.
Ta có: \(\left| {\overrightarrow {AB} {\rm{ \;}} + \overrightarrow {AC} } \right| = \left| {2\overrightarrow {AM} } \right| = 2AM = 2\sqrt {A{B^2} + B{M^2}} {\rm{ \;}} = 2\sqrt {{a^2} + {{\left( {\frac{a}{2}} \right)}^2}} {\rm{ \;}} = a\sqrt 5 \).
Chọn D.
Câu 3 (TH):
Hướng dẫn:
Biến đổi \(\overrightarrow {MA} {\rm{ \;}} – \overrightarrow {MB} {\rm{ \;}} + \overrightarrow {MC} {\rm{ \;}} = \vec 0\) về hai vectơ bằng nhau.
Xác định vị trí điểm M dựa vào điều kiện vừa tìm được.
Cách giải:
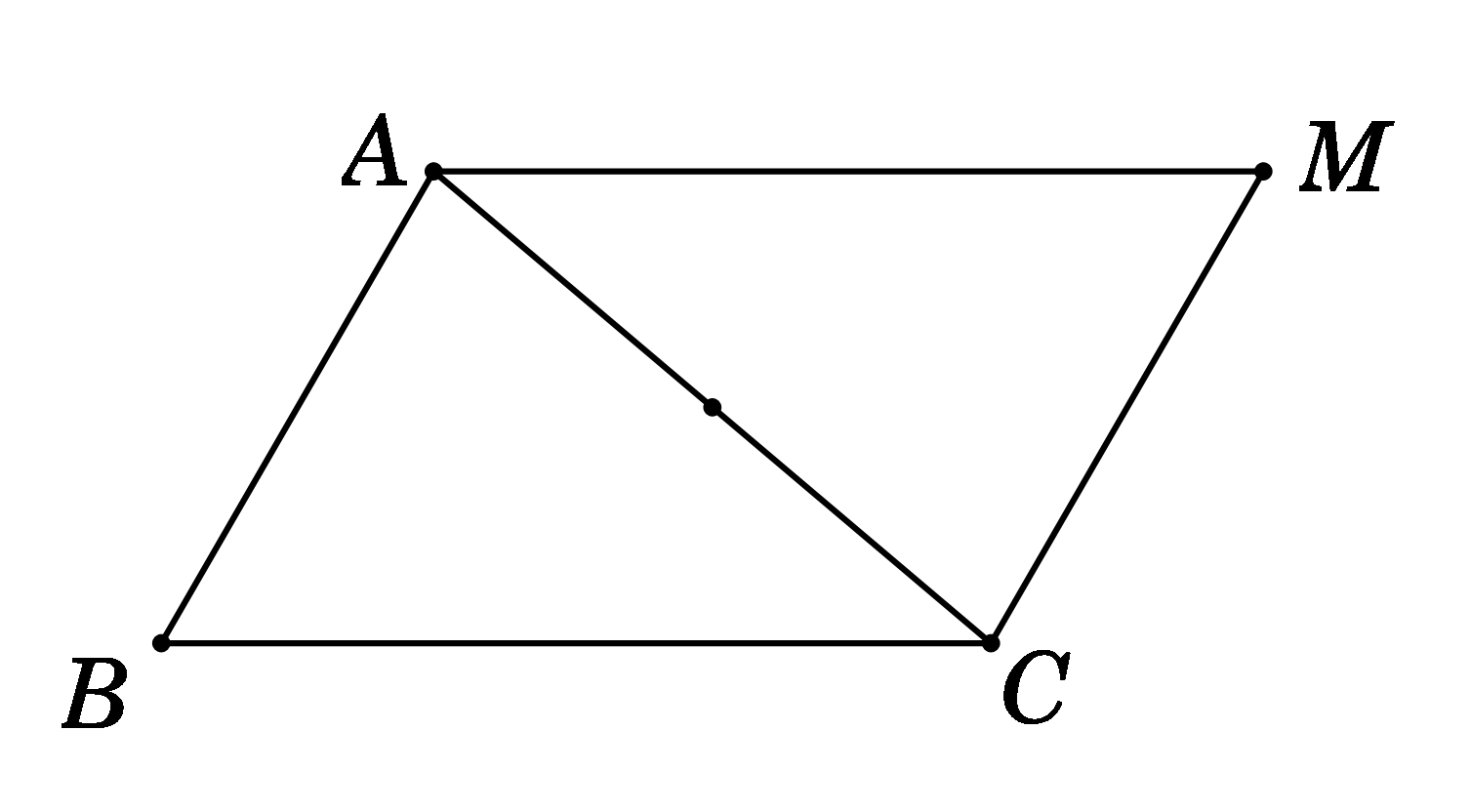
Ta có \(\overrightarrow {MA} {\rm{ \;}} – \overrightarrow {MB} {\rm{ \;}} + \overrightarrow {MC} {\rm{ \;}} = \vec 0\)\( \Leftrightarrow \overrightarrow {BA} {\rm{ \;}} + \overrightarrow {MC} {\rm{ \;}} = \vec 0{\rm{ \;}} \Leftrightarrow \overrightarrow {MC} {\rm{ \;}} = \overrightarrow {AB} \)
\( \Rightarrow \) MABC là hình bình hành.
Chọn A.
Câu 4 (NB):
Hướng dẫn:
Sử dụng định lí cosin trong tam giác tại đỉnh C: \({c^2} = {a^2} + {b^2} – 2ab\cos C\).
Cách giải:
Ta có: \({c^2} = {a^2} + {b^2} – 2ab\cos C\).
\(\begin{array}{*{20}{l}}{ \Rightarrow A{B^2} = B{C^2} + A{C^2} – 2BC.AC.\cos C}\\{ \Rightarrow 5 = B{C^2} + 2 – 2.BC.\sqrt 2 .\frac{{\sqrt 2 }}{2}}\\{ \Leftrightarrow B{C^2} – 2BC – 3 = 0}\\{ \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{BC = 3{\mkern 1mu} {\mkern 1mu} \left( {tm} \right)}\\{BC = {\rm{ \;}} – 1{\mkern 1mu} {\mkern 1mu} \left( {ktm} \right)}\end{array}} \right.}\end{array}\)
Vậy BC = 3.
Chọn A.
Câu 5 (NB):
Hướng dẫn:
Cặp số nào thỏa mãn bất phương trình là nghiệm của bất phương trình.
Cách giải:
Thay cặp số (x;y) = (0;4) vào bất phương trình: 0 – 2.4 + 5 > 0 => Sai.
Thay cặp số (x;y) = (2;5) vào bất phương trình: 2 – 2. 5 + 5 > 0 => Sai.
Thay cặp số (x;y) = (2;3) vào bất phương trình: 2 – 2.3 + 5 > 0 => Đúng.
Thay cặp số (x;y) = (1;4) vào bất phương trình: 1 – 2.4 + 5 > 0 => Sai.
Chọn C.
Câu 6 (TH):
Hướng dẫn:
Biến đổi \(\overrightarrow {MA} {\rm{ \;}} – \overrightarrow {MB} {\rm{ \;}} + \overrightarrow {MC} {\rm{ \;}} = \vec 0\) về hai vectơ bằng nhau.
Xác định vị trí điểm M dựa vào điều kiện vừa tìm được.
Cách giải:
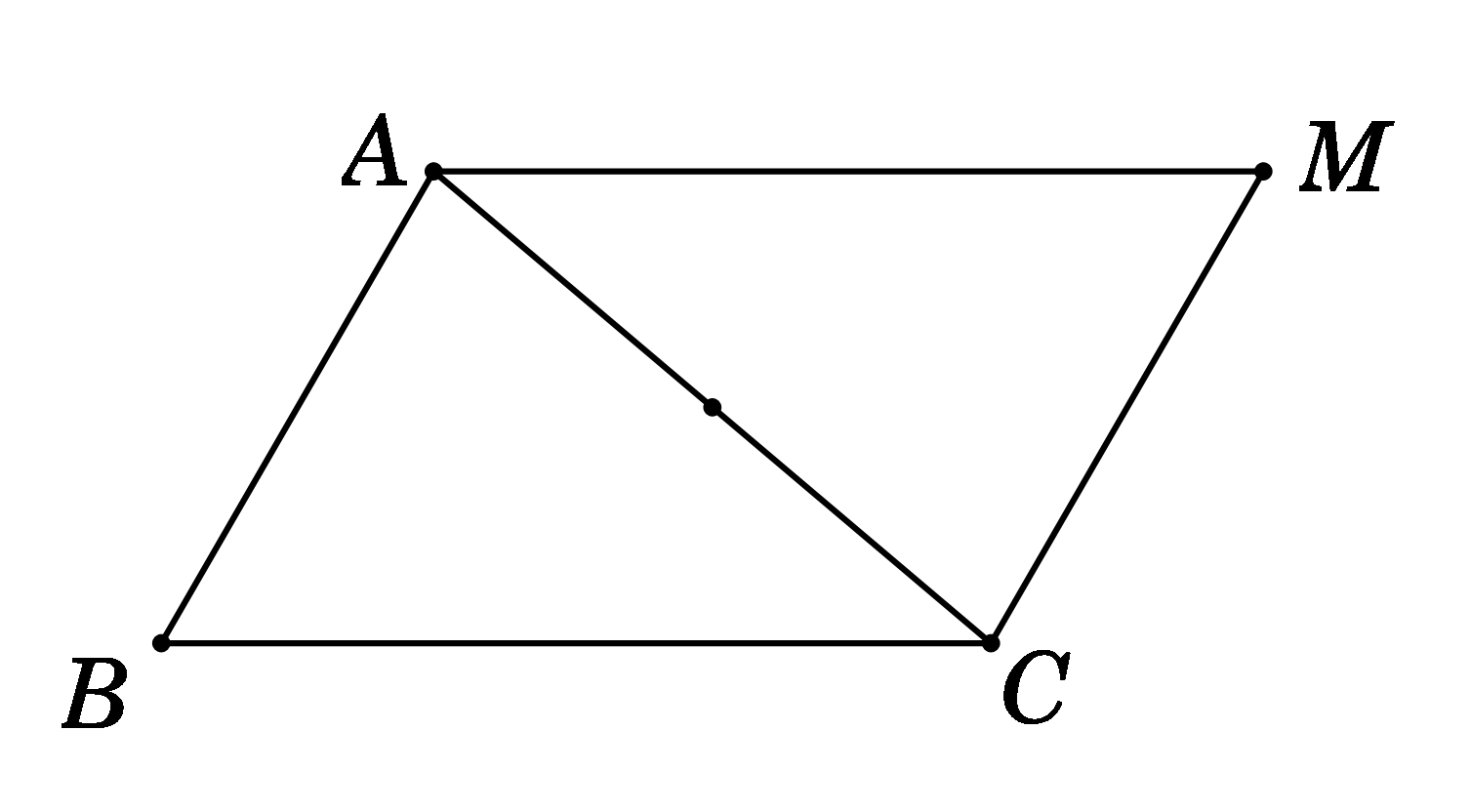
Ta có \(\overrightarrow {MA} {\rm{ \;}} – \overrightarrow {MB} {\rm{ \;}} + \overrightarrow {MC} {\rm{ \;}} = \vec 0\)\( \Leftrightarrow \overrightarrow {BA} {\rm{ \;}} + \overrightarrow {MC} {\rm{ \;}} = \vec 0{\rm{ \;}} \Leftrightarrow \overrightarrow {MC} {\rm{ \;}} = \overrightarrow {AB} \)
\( \Rightarrow \) MABC là hình bình hành.
Chọn A.
Câu 7 (NB):
Hướng dẫn:
Tính \(\angle C = {180^0} – \left( {\angle A + \angle B} \right)\).
Sử dụng định lí sin: \(\frac{c}{{\sin C}} = 2R\).
Cách giải:
Ta có: \(\angle C = {180^0} – \left( {\angle A + \angle B} \right) = {60^0}\).
Áp dụng định lí sin ta có: \(\frac{c}{{\sin C}} = 2R \Rightarrow R = \frac{c}{{2\sin C}} = \frac{6}{{2\sin {{60}^0}}} = 2\sqrt 3 \).
Chọn B.
Câu 8 (NB):
Hướng dẫn:
Thay giá trị x=4 vào hàm số có công thức tương ứng.
Cách giải:
Ta có: \(4 \in (2;5]\) nên \(f(4) = {4^2} – 1 = 15.\)
Chọn B.
Câu 9 (TH):
Hướng dẫn:
Giải phương trình, bất phương trình.
Xác định tập hợp \(A\), \(B\) bằng phương pháp liệt kê phần tử, đưa về cách viết khoảng, nửa khoảng.
Xác định \(A \cap B\); \(A \cup B\); \(A\backslash B\); \(B\backslash A\).
Cách giải:
*) \({x^2} – 7x + 6 = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{x – 1 = 0}\\{x – 6 = 0}\end{array}} \right. \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{x = 1}\\{x = 6}\end{array}} \right.\) (thỏa mãn)
\( \Rightarrow A = \left\{ {1;{\mkern 1mu} {\mkern 1mu} 6} \right\}\)
*) \(\left| x \right| > 4 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{x 4}\end{array}} \right.\)\( \Rightarrow x \in \left( { – \infty ;{\mkern 1mu} – 4} \right) \cup \left( {4;{\mkern 1mu} + \infty } \right)\)
\( \Rightarrow B = \left( { – \infty ;{\mkern 1mu} – 4} \right) \cup \left( {4;{\mkern 1mu} + \infty } \right)\)
Ta có:
\(A \cup B = \left( { – \infty ;{\mkern 1mu} – 4} \right) \cup \left\{ 1 \right\} \cup \left( {4;{\mkern 1mu} + \infty } \right)\) , \(A \cap B = \left\{ 6 \right\}\)
\(B\backslash A = \left( { – \infty ;{\mkern 1mu} – 4} \right) \cup \left( {4;{\mkern 1mu} {\mkern 1mu} 6} \right) \cup \left( {6; + \infty } \right)\), \(A\backslash B = \left\{ 1 \right\}\)
Vậy đáp án đúng là: \(\left( {A\backslash B} \right) \subset A\)
Chọn C.
Câu 10 (TH):
Hướng dẫn:
Sử dụng khái niệm các phép toán trên tập hợp.
Cách giải:
Dễ thấy phần tô màu không thuộc A nên loại đáp án A, B.
Phần tô màu trong hình vẽ biểu diễn cho tập hợp \(\left( {B \cap C} \right)\backslash A.\)
Chọn D.
Câu 11 (TH):
Hướng dẫn:
Tính PR và QR theo h = AR và \(\tan \alpha {\rm{ \;}} = \tan {65^0},{\mkern 1mu} {\mkern 1mu} \tan \beta {\rm{ \;}} = \tan {79^0}\).
Sử dụng d = PQ = PR – QR, tính d.
Tính chiều cao tòa nhà bằng d + RO.
Cách giải:
Đặt d = PQ = LM = 50m, h = AR là chiều cao từ giác kế đến đỉnh tòa nhà.
Ta có: \(\angle APR = \alpha {\rm{ \;}} = {65^0},{\mkern 1mu} {\mkern 1mu} \angle AQR = \beta {\rm{ \;}} = {79^0}\).
Gọi \({d_1} = PR = \frac{h}{{\tan \alpha }},{\mkern 1mu} {\mkern 1mu} {d_2} = QR = \frac{h}{{\tan \beta }}\), ta có:
\(\begin{array}{*{20}{l}}{d = {d_1} – {d_2} = \frac{h}{{\tan \alpha }} – \frac{h}{{\tan \beta }} = h\left( {\frac{1}{{\tan \alpha }} – \frac{1}{{\tan \beta }}} \right)}\\{ \Rightarrow h = \frac{d}{{\frac{1}{{\tan \alpha }} – \frac{1}{{\tan \beta }}}} = \frac{{50}}{{\frac{1}{{\tan {{65}^0}}} – \frac{1}{{\tan {{79}^0}}}}} \approx 183,9{\mkern 1mu} {\mkern 1mu} \left( m \right)}\end{array}\)
Vậy chiều cao của tòa nhà là AR + RO \( \approx 183,9 + 1,4 = 185,3{\mkern 1mu} {\mkern 1mu} \left( m \right)\).
Chọn D.
Câu 12 (TH):
Hướng dẫn:
Dùng công thức \({\sin ^2}x + {\cos ^2}x = 1\) để tính cos x
Cách giải:
Hàm số \(y = \frac{{3x – 1}}{{\sqrt {2x – 2} }}\) xác định khi \(\left\{ \begin{array}{l}\sqrt {2x – 2} \ne 0\\2x – 2 \ge 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x \ne 1\\x \ge 1\end{array} \right. \Leftrightarrow x > 1\)
Vậy tập xác định \({\rm{D}} = \left( {1; + \infty } \right).\)
Chọn C.
Câu 13 (TH):
Hướng dẫn:
Lập bảng biến thiên, suy ra các khoản đồng biến nghịch biến.
Cách giải:
Hàm số \(y = – {x^2} + 4x + 1\) có \(a = – 1,b = 4\)
Đỉnh của parabol: \({x_I} = – \frac{b}{{2a}} = 2,{y_I} = – {2^2} + 4.2 + 1 = 5.\)
Bảng biến thiên của hàm số:
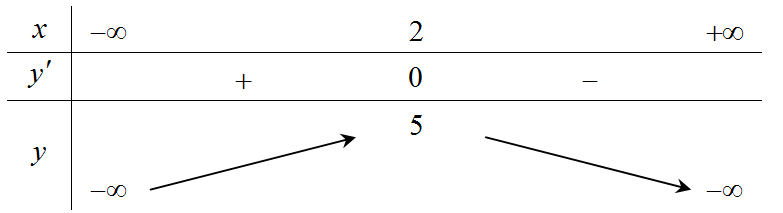
Dựa vào bảng biến thiên suy ra khẳng định D sai.
Chọn D.
Câu 14 (TH):
Hướng dẫn:
Tìm \({\sin ^2}\alpha \) dựa vào đẳng thức \({\sin ^2}\alpha + {\cos ^2}\alpha = 1\)
Chia cả tử và mẫu của P cho \(\sin \alpha \), tính P theo \(\cos \alpha \) và \({\sin ^2}\alpha \).
Cách giải:
Chia cả tử và mẫu cho \(\sin \alpha {\rm{ \;}} \ne 0\) ta được:
\(\begin{array}{*{20}{l}}{P = \frac{{\tan \alpha {\rm{ \;}} + 2\cot \alpha }}{{2\tan \alpha {\rm{ \;}} + 3\cot \alpha }}}\\{P = \frac{{\frac{1}{{\cos \alpha }} + \frac{{2\cos \alpha }}{{{{\sin }^2}\alpha }}}}{{\frac{2}{{\cos \alpha }} + \frac{{3\cos \alpha }}{{{{\sin }^2}\alpha }}}}}\end{array}\)
Ta có:
\(\begin{array}{*{20}{l}}{{{\sin }^2}\alpha {\rm{ \;}} + {{\cos }^2}\alpha {\rm{ \;}} = 1}\\{ \Rightarrow {{\sin }^2}\alpha {\rm{ \;}} + {{\left( {\frac{1}{4}} \right)}^2} = 1}\\{ \Leftrightarrow {{\sin }^2}\alpha {\rm{ \;}} = \frac{{15}}{{16}}}\end{array}\)
Khi đó: \(P = \frac{{\frac{1}{{\frac{1}{4}}} + \frac{{2.\frac{1}{4}}}{{\frac{{15}}{{16}}}}}}{{\frac{2}{{\frac{1}{4}}} + \frac{{3.\frac{1}{4}}}{{\frac{{15}}{{16}}}}}} = \frac{{\frac{{68}}{{15}}}}{{\frac{{44}}{5}}} = \frac{{17}}{{33}}\).
Chọn B.
Câu 15 (TH):
Hướng dẫn:
Vì vật đứng yên nên \(\overrightarrow {{F_1}} {\rm{ \;}} + \overrightarrow {{F_2}} {\rm{ \;}} + \overrightarrow {{F_3}} {\rm{ \;}} = \vec 0\).
Xác định \(\left| {\overrightarrow {{F_3}} } \right| = \left| {\overrightarrow {{F_1}} {\rm{ \;}} + \overrightarrow {{F_2}} } \right|\), dựa vào tam giác MAB đều.
Cách giải:
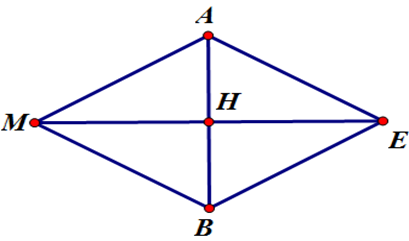
Ta có tam giác MAB đều.
Do vật đứng yên nên ta có: \(\overrightarrow {{F_1}} {\rm{ \;}} + \overrightarrow {{F_2}} {\rm{ \;}} + \overrightarrow {{F_3}} {\rm{ \;}} = \vec 0\)\( \Rightarrow \overrightarrow {{F_3}} {\rm{ \;}} = {\rm{ \;}} – (\overrightarrow {{F_1}} {\rm{ \;}} + \overrightarrow {{F_2}} )\)\( \Rightarrow \left| {\overrightarrow {{F_3}} } \right| = \left| {\overrightarrow {{F_1}} {\rm{ \;}} + \overrightarrow {{F_2}} } \right|\)
\( \Rightarrow \left| {\overrightarrow {{F_3}} } \right| = \left| {\overrightarrow {MA} {\rm{ \;}} + \overrightarrow {MB} } \right| = \left| {\overrightarrow {ME} } \right| = 2MH = 2.50\frac{{\sqrt 3 }}{2} = 50\sqrt 3 \)
(với MAEB là hình bình hành tâm \(H\)).
Chọn C.
Câu 16 (TH):
Hướng dẫn:
Đặt \(\overrightarrow {AB} {\rm{ \;}} = \vec u\), \(\overrightarrow {BC} {\rm{ \;}} = \vec v\) suy ra \(\vec u + \vec v = \overrightarrow {AB} {\rm{ \;}} + \overrightarrow {BC} {\rm{ \;}} = \overrightarrow {AC} \).
Xét các trường hợp A, B, C thẳng hàng; A, B, C không thẳng hàng.
Ngoài ra, có thể chỉ ra các đáp án sai bằng cách chỉ ra một trường hợp mà mệnh đề đó không đúng.
Cách giải:
Đặt \(\overrightarrow {AB} {\rm{ \;}} = \vec u\), \(\overrightarrow {BC} {\rm{ \;}} = \vec v\) khi đó ta có \(\vec u + \vec v = \overrightarrow {AB} {\rm{ \;}} + \overrightarrow {BC} {\rm{ \;}} = \overrightarrow {AC} \)
Nếu A,B,C thẳng hàng và \(B\) nằm giữa A,C thì \(\left| {\vec u + \vec v} \right| = \left| {\vec u} \right| + \left| {\vec v} \right|\)
Nếu A,B,C thẳng hàng và \(B\)không nằm giữa A,C thì \(\left| {\vec u + \vec v} \right| < \left| {\vec u} \right| + \left| {\vec v} \right|\)
Nếu A,B,C không thẳng hàng thì trong tam giác ABC có \(AB + BC > AC\). Suy ra \(\left| {\vec u + \vec v} \right| < \left| {\vec u} \right| + \left| {\vec v} \right|\)
Do đó \(\left| {\vec u + \vec v} \right| \le \left| {\vec u} \right| + \left| {\vec v} \right|\)
Từ đó suy ra, đáp án B đúng
Đáp án A, C sai vì chọn \(\vec v = \vec 0\) thì có \(\left| {\vec u + \vec w} \right| \ge \left| {\vec u} \right| + \left| {\vec w} \right|\) (sai theo chứng minh ở trên).
Đáp án D sai vì chọn \(\vec u = \vec 0\) và \(\vec v \ne \vec 0\) thì có \(\left| {\vec v} \right| \le {\rm{ \;}} – \left| {\vec v} \right|\)\( \Rightarrow \) vô lý vì độ dài véctơ khác vectơ-không là một số dương.
Chọn A.
Câu 17 (VD):
Cách giải:
Hàm số có hoành độ đỉnh \({x_I} = – \frac{b}{{2a}} = 1\), tung độ đỉnh \({y_I} = a{.1^2} + b.1 + c = 1\)
Điểm \(A(2;3)\) thuộc đồ thị nên \(a{.2^2} + b.2 + c = 3\) hay \(4a + 2b + c = 3\)
Từ đó ta có hệ \(\left\{ {\begin{array}{*{20}{c}}{a + b + c = 1}\\{4a + 2b + c = 3}\\{ – \frac{b}{{2a}} = 1}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{a + b + c = 1}\\{4a + 2b + c = 3}\\{2a + b = 0}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{a = 2}\\{b = – 4}\\{c = 3}\end{array}} \right.\)
Suy ra \(S = {a^2} + {b^2} + {c^2}\)=29
Chọn C.
Câu 18 (TH):
Cách giải:
Đồ thị hàm số có bề lõm hướng lên \( \Rightarrow a > 0\).
Đồ thị hàm số cắt \(Oy\)tại điểm có tung độ âm \( \Rightarrow c < 0\). Loại A, C.
Đồ thị hàm số có trục đối xứng bên trái \(Oy\): \( \Rightarrow – \frac{b}{{2a}} 0\). Loại B.
Chọn D.
Câu 19 (TH):
Hướng dẫn:
Sử dụng công thức: \(\overrightarrow {BA} .\overrightarrow {BC} {\rm{ \;}} = BA.BC.\cos \angle \left( {\overrightarrow {BA} ,\overrightarrow {BC} } \right).\)
Cách giải:
Vì ABC là tam giác vuông cân tại A nên \(BC = AB\sqrt 2 {\rm{ \;}} = 6\sqrt 2 \) và \(\left( {\overrightarrow {BA} ,\overrightarrow {BC} } \right) = \angle ABC = {45^0}\).
Vậy \(\overrightarrow {BA} .\overrightarrow {BC} {\rm{ \;}} = BA.BC.\cos \angle \left( {\overrightarrow {BA} ,\overrightarrow {BC} } \right)\)
\( = 6.6\sqrt 2 .\cos {45^0} = 6.6\sqrt 2 .\frac{{\sqrt 2 }}{2} = 36.\)
Chọn B.
Câu 20 (VD):
Hướng dẫn:
Sử dụng công thức \(n\left( {A \cup B} \right) = n\left( A \right) + n\left( B \right) – n\left( {A \cap B} \right)\).
Cách giải:
Gọi A là tập hợp các bạn đăng kí tiết mục múa \( \Rightarrow n\left( A \right) = 9.\)
B là tập hợp các bạn đăng kí tiết mục diễn kịch \( \Rightarrow n\left( B \right) = 13.\)
\( \Rightarrow A \cap B:\) tập hợp các bạn đăng kí cả 2 tiết mục múa và diễn kịch \( \Rightarrow n\left( {A \cap B} \right) = 4.\)
\(A \cup B\): tập hợp các bạn tham gia ít nhất 1 tiết mục.
Ta có: \(n\left( {A \cup B} \right) = n\left( A \right) + n\left( B \right) – n\left( {A \cap B} \right)\)
\( \Rightarrow \) Số học sinh lớp 10A tham gia văn nghệ là: \(n\left( {A \cup B} \right) = 9 + 13 – 4 = 18.\)
Chọn B.
Câu 21 (NB):
Hướng dẫn:
Xét điểm gốc tọa độ để xác định miền nghiệm của bất phương trình.
Cách giải:
Thay \(x = 0,y = 0\) vào BPT \(2x – 3y + 6 \ge 0\) ta được: \(2.0 – 3.0 + 6 \ge 0\) (đúng)
Nên O(0,0) thuộc miền nghiệm nên
Miền nghiệm nửa mặt phẳng có bờ là d chứa gốc tọa độ O và có lấy đường thẳng d
Chọn A.
Câu 22 (NB):
Hướng dẫn:
Vẽ đồ thị hoặc thử các đáp án
Cách giải:
Xét hệ bất phương trình \(\left\{ {\begin{array}{*{20}{l}}{x + 2y > – 3\quad (1)}\\{3x – y 0\quad (3)}\end{array}} \right.\).
\(\left( { – 2; – 1} \right)\) không thỏa mãn BPT (3)
\(\left( {2;0} \right)\) không thỏa mãn BPT (3)
\(\left( {3;2} \right)\) không thỏa mãn BPT (2)
\(\left( {0,2} \right)\)thỏa mãn cả 3 BPT nên là nghiệm của hệ.
Chọn D.
Câu 23 (TH):
Hướng dẫn:
Nhóm thích hợp, sử dụng mối quan hệ giá trị lượng giác của hai góc bù nhau: \(\cos \left( {{{180}^0} – \alpha } \right) = {\rm{ \;}} – \cos \alpha \).
Cách giải:
\(\begin{array}{*{20}{l}}{B = \cos {0^0} + \cos {{20}^0} + \cos {{40}^0} + … + \cos {{160}^0} + \cos {{180}^0}}\\{B = \left( {\cos {0^0} + \cos {{180}^0}} \right) + \left( {\cos {{20}^0} + \cos {{160}^0}} \right) + \left( {\cos {{40}^0} + \cos {{140}^0}} \right) + … + \left( {\cos {{80}^0} + \cos {{100}^0}} \right)}\\{B = \left( {\cos {0^0} – \cos {0^0}} \right) + \left( {\cos {{20}^0} – \cos {{20}^0}} \right) + \left( {\cos {{40}^0} – \cos {{40}^0}} \right) + … + \left( {\cos {{80}^0} – \cos {{80}^0}} \right)}\\{B = 0}\end{array}\)
Chọn A
Câu 24 (TH):
Hướng dẫn:
Sử dụng công thức \(\overrightarrow {BM} .\overrightarrow {BA} {\rm{ \;}} = BM.BA.\cos \left( {\overrightarrow {BM} ,\overrightarrow {BA} } \right).\)
Cách giải:
Ta có: \(\overrightarrow {BM} .\overrightarrow {BA} {\rm{ \;}} = {\rm{ \;}} – \frac{1}{3}\overrightarrow {BC} .\overrightarrow {BA} {\rm{ \;}} = {\rm{ \;}} – \frac{1}{3}BC.BA.\cos \left( {\overrightarrow {BC} ,\overrightarrow {BA} } \right).\)
Vì tam giác ABC đều nên \(\cos \left( {\overrightarrow {BC} ,\overrightarrow {BA} } \right) = \angle ABC = {60^0}\).
\( \Rightarrow \overrightarrow {BM} .\overrightarrow {BA} = – \frac{1}{3}.6.6.\frac{{\sqrt 3 }}{2} = {\rm{ \;}} – 6\sqrt 3 .\)
Chọn B.
Câu 25 (TH):
Cách giải:
Ta có \(\Delta = {1^2} – 4.\left( { – 3} \right).2 = 25\)
Vì \(a = – 3 < 0\) nên hàm số có giá trị lớn nhất là: \(\frac{{ – \Delta }}{{4a}} = \frac{{25}}{{12}}\).
Chọn A.
Phần 2: Tự luận (4 điểm)
Câu 1 (VD):
Hướng dẫn:
a) Sử dụng quy tắc hiệu, đưa về tính chất vectơ trọng tâm tam giác.
b) Sử dụng tính chất vectơ trung tuyến.
Cách giải:
a) Ta có:
\(\begin{array}{*{20}{l}}{\overrightarrow {KA} {\rm{ \;}} + 2\overrightarrow {KB} {\rm{ \;}} = \overrightarrow {CB} }\\{ \Leftrightarrow \overrightarrow {KA} {\rm{ \;}} + 2\overrightarrow {KB} {\rm{ \;}} = \overrightarrow {KB} {\rm{ \;}} – \overrightarrow {KC} }\\{ \Leftrightarrow \overrightarrow {KA} {\rm{ \;}} + \overrightarrow {KB} {\rm{ \;}} + \overrightarrow {KC} {\rm{ \;}} = \vec 0}\end{array}\)
Vậy K là trọng tâm tam giác ABC.
b) Gọi I là trung điểm của BC ta có:
\(\begin{array}{l}\overrightarrow {MA} + 2\overrightarrow {MB} + 2\overrightarrow {MC} = \overrightarrow 0 \\ \Leftrightarrow \overrightarrow {MA} + 2\left( {\overrightarrow {MB} + \overrightarrow {MC} } \right) = \overrightarrow 0 \\ \Leftrightarrow \left( {\overrightarrow {MI} + \overrightarrow {IA} } \right) + 4\overrightarrow {MI} = \overrightarrow 0 \\ \Leftrightarrow 5\overrightarrow {MI} + \overrightarrow {IA} = 0\\ \Leftrightarrow \overrightarrow {IM} = \frac{1}{5}\overrightarrow {IA} \end{array}\)
Vậy M là thuộc IA sao cho \(IM = \frac{1}{5}IA\).
Câu 2 (VD):
Cách giải:
Ta có \(A\left( {1;4} \right)\) và \(I\left( {2;5} \right)\) thuộc parabol nên \(\left\{ \begin{array}{l}a + b + c = 4\\4a + 2b + c = 5\end{array} \right.\)
Lại có hoành độ đỉnh \({x_I} = – \frac{b}{{2a}} = 2 \Rightarrow b = – 4a\)
Từ đó ta có hệ \(\left\{ \begin{array}{l}a + b + c = 4\\4a + 2b + c = 5\\b + 4a = 0\end{array} \right. \Leftrightarrow a = – 1;b = 4;c = 1\)
Vậy parabol đó là \(y = – {x^2} + 4x + 1\)
* Xét sự biến thiên
Parabol (P) có \(a = – 1 < 0\) và đỉnh là \(I\left( {2;5} \right)\)
Bảng biến thiên
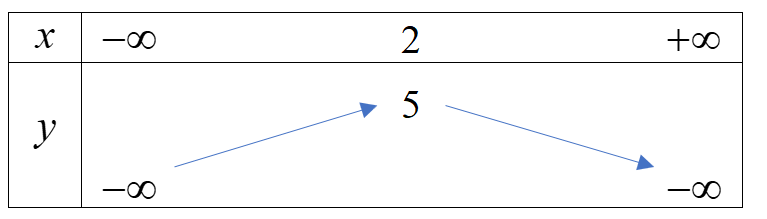
Hàm số đồng biến trên \(( – \infty ;2)\) và nghịch biến trên \((2; + \infty )\).
Câu 3 (VDC):
Hướng dẫn:
a) Áp dụng định lí cosin và định lí sin
b) Áp dụn định lí cosin và công thức \(\cos A = 1 – 2{\sin ^2}\frac{A}{2}\)
Cách giải:
a) Áp dụng định lí cosin và định lí sin ta có:
\(\cos A = \frac{{{b^2} + {c^2} – {a^2}}}{{2bc}};\sin A = \frac{a}{{2R}}\)
\( \Rightarrow \cot A = \frac{{\cos A}}{{\sin A}} = \frac{{{b^2} + {c^2} – {a^2}}}{{2bc}}.\frac{{2R}}{a} = \frac{{{b^2} + {c^2} – {a^2}}}{{abc}}R\)
Tương tự ta cũng có: \(\cot B = \frac{{{a^2} + {c^2} – {b^2}}}{{abc}}R;\cot C = \frac{{{a^2} + {b^2} – {c^2}}}{{abc}}R\)
\(\begin{array}{l} \Rightarrow \cot A + \cot B + \cot C = \frac{{{b^2} + {c^2} – {a^2}}}{{abc}}R + \frac{{{a^2} + {c^2} – {b^2}}}{{abc}}R + \frac{{{a^2} + {b^2} – {c^2}}}{{abc}}R\\ = \frac{R}{{abc}}({b^2} + {c^2} – {a^2} + {a^2} + {c^2} – {b^2} + {a^2} + {b^2} – {c^2})\\ = \frac{R}{{abc}}({a^2} + {b^2} + {c^2}) = \frac{{{a^2} + {b^2} + {c^2}}}{{abc}}R\end{array}\)
b) Ta có: \(\cos A = \frac{{{b^2} + {c^2} – {a^2}}}{{2bc}}\)
Mà \(\cos A = 1 – 2{\sin ^2}\frac{A}{2} \Rightarrow \sin \frac{A}{2} = \sqrt {\frac{{1 – \cos A}}{2}} \) (do \({0^ \circ } < \frac{A}{2} < {90^ \circ }\))
\(\begin{array}{l} \Rightarrow \sin \frac{A}{2} = \sqrt {\frac{{1 – \frac{{{b^2} + {c^2} – {a^2}}}{{2bc}}}}{2}} \\ \Leftrightarrow \sin \frac{A}{2} = \sqrt {\frac{{{a^2} – \left( {{b^2} + {c^2} – 2bc} \right)}}{{4bc}}} \\ \Leftrightarrow \sin \frac{A}{2} = \sqrt {\frac{{{a^2} – {{(b – c)}^2}}}{{4bc}}} \\ \Leftrightarrow \sin \frac{A}{2} = \sqrt {\frac{{(a – b + c)(a + b – c)}}{{4bc}}} \end{array}\)
Lại có: \(p = \frac{{a + b + c}}{2}\)\( \Rightarrow p – b = \frac{{a – b + c}}{2};p – c = \frac{{a + b – c}}{2}\)
\(\begin{array}{l} \Leftrightarrow \frac{{(a – b + c)(a + b – c)}}{4} = (p – b)(p – c)\\ \Leftrightarrow \sin \frac{A}{2} = \sqrt {\frac{{(p – b)(p – c)}}{{bc}}} \end{array}\)