Trả lời Giải đề 2 Tổng hợp 10 đề thi học kì 1 Toán 10 Cánh diều – Đề thi đề kiểm tra Toán lớp 10 Cánh diều.
Câu hỏi/Đề bài:
HƯỚNG DẪN GIẢI CHI TIẾT
I. Phần trắc nghiệm
|
1.B |
2.C |
3.B |
4.D |
5.D |
6.D |
7.A |
8.D |
9.B |
10.A |
|
11.A |
12.C |
13.D |
14.A |
15.B |
16.D |
17.A |
18.D |
19.A |
20.B |
|
21.A |
22.C |
23.D |
24.C |
25.D |
26.B |
27.B |
28.A |
29.A |
30.C |
Câu 1 (NB):
Hướng dẫn:
Thay tọa độ từng điểm vào hệ bất phương trình.
Cách giải:
Ta có \(\left\{ {\begin{array}{*{20}{l}}{3x – 4y + 12 \ge 0}\\{x + y – 5 \ge 0}\\{x + 1 > 0}\end{array}} \right.\), kiểm tra đáp án thấy \(N\left( {4{\mkern 1mu} ;{\mkern 1mu} 3} \right)\) thoả mãn.
Chọn B.
Câu 2 (NB):
Hướng dẫn:
Hàm phân thức xác định khi mẫu thức khác 0.
Cách giải:
ĐKXĐ: \(2x – 2 \ne 0 \Leftrightarrow x \ne 1\).
Vậy TXĐ của hàm số là \(D = \mathbb{R}\backslash \left\{ 1 \right\}\).
Chọn C.
Câu 3 (NB):
Cách giải:
\(f(4) = {4^2} – 1 = {\rm{\;}}15\)
Chọn B.
Câu 4 (NB):
Hướng dẫn:
Đồ thị hàm số \(y = a{x^2} + bx + c\) có trục đối xứng là đường thẳng \(x = {\rm{ \;}} – \frac{b}{{2a}}\).
Với a < 0: Hàm số đồng biến trên \(\left( { – \infty ; – \frac{b}{{2a}}} \right)\) và nghịch biến trên \(\left( { – \frac{b}{{2a}}; + \infty } \right)\).
Cách giải:
Vì a < 0 nên hàm số đồng biến trên \(\left( { – \infty ; – \frac{b}{{2a}}} \right)\) và nghịch biến trên \(\left( { – \frac{b}{{2a}}; + \infty } \right)\). Do đó A và B sai.
Đồ thị có trục đối xứng là đường thẳng \(x = {\rm{ \;}} – \frac{b}{{2a}}\) nên D đúng.
Chưa đủ dữ kiện để xác định số giao điểm của đồ thị hàm số với trục hoành nên C sai.
Chọn D.
Câu 5 (NB):
Hướng dẫn:
Hàm số bậc hai có dạng \(y = a{x^2} + bx + c{\mkern 1mu} {\mkern 1mu} \left( {a \ne 0} \right)\).
Cách giải:
Hàm số \(y = \left( {m – 4} \right){x^2} – 3x + 2\) là hàm số bậc hai khi \(m – 4 \ne 0 \Leftrightarrow m \ne 4\).
Chọn D.
Câu 6 (NB):
Hướng dẫn:
Áp dụng quy tắc dấu của tam thức bậc hai.
Cách giải:
\(f(x) = a{x^2} + bx + c{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} (a \ne 0)\), \(f(x) \le 0,\forall x \in \mathbb{R}\)\( \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{a < 0}\\{\Delta {\rm{ \;}} \le 0}\end{array}} \right.\).
Chọn D.
Câu 7 (NB):
Hướng dẫn:
Vectơ-không cùng phương với mọi vectơ.
Cách giải:
Vectơ-không cùng phương với mọi vectơ.
Chọn A.
Câu 8 (NB):
Hướng dẫn:
Xét từng đáp án.
Sử dụng công thức hình bình hành, các tính chất của phép cộng vectơ
Cách giải:
Ta có: \(\overrightarrow {DA} {\rm{ \;}} + \overrightarrow {DB} {\rm{ \;}} + \overrightarrow {DC} {\rm{ \;}} = \left( {\overrightarrow {DA} {\rm{ \;}} + \overrightarrow {DC} } \right) + \overrightarrow {DB} {\rm{ \;}} = \overrightarrow {DB} {\rm{ \;}} + \overrightarrow {DB} {\rm{ \;}} = 2\overrightarrow {DB} {\rm{ \;}} \ne \vec 0\).
Chọn D.
Câu 9 (NB):
Hướng dẫn:
Sử dụng quy tắc cộng vectơ.
Cách giải:
Với ba điểm A,B,C phân biệt ta có: \(\overrightarrow {CA} {\rm{ \;}} + \overrightarrow {AB} {\rm{ \;}} = \overrightarrow {CB} \).
Vậy đáp án B sai
Chọn B.
Câu 10 (NB):
Hướng dẫn:
Áp dụng tính chất của hình bình hành.
Cách giải:
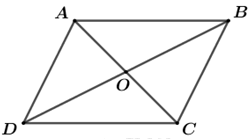
Vì ABCD là hình bình hành nên \(AB = DC,{\mkern 1mu} {\mkern 1mu} AD = BC,{\mkern 1mu} {\mkern 1mu} AO = \frac{1}{2}AC\).
Do vậy các đáp án đúng là: \(\left| {\overrightarrow {BC} } \right| = \left| {\overrightarrow {DA} } \right|\), \(\left| {\overrightarrow {AB} } \right| = \left| {\overrightarrow {CD} } \right|\), \(\left| {\overrightarrow {AO} } \right| = \frac{1}{2}\left| {\overrightarrow {CA} } \right|\)
\(\left| {\overrightarrow {AC} } \right| = \left| {\overrightarrow {BD} } \right|\) là đáp án sai vì AC và BD là hai đường chéo của hình bình hành ABCD nên \(AC \ne BD\).
Chọn A.
Câu 11 (NB):
Hướng dẫn:
Áp dụng công thức: \(\vec a.\vec b = \left| {\vec a} \right|.\left| {\vec b} \right|.\cos \left( {\vec a,{\mkern 1mu} {\mkern 1mu} \vec b} \right)\)
Hai vecto cùng hướng thì góc giữa hai vecto bằng \({0^0}\).
Cách giải:
Ta có: \(\vec a \cdot \vec b = \)\(\left| {\vec a} \right|{\mkern 1mu} \cdot \left| {\vec b} \right| \cdot \cos \left( {\vec a,{\mkern 1mu} {\mkern 1mu} \vec b} \right)\)
Do \(\vec a\) và \(\vec b\) là hai vecto cùng hướng nên \(\left( {\vec a,{\mkern 1mu} {\mkern 1mu} \vec b} \right) = {0^^\circ }\)\( \Rightarrow \cos \left( {\vec a,{\mkern 1mu} {\mkern 1mu} \vec b} \right) = 1\).
\( \Rightarrow \vec a \cdot \vec b = \left| {\vec a} \right|{\mkern 1mu} \cdot \left| {\vec b} \right|\)
Vậy \(\vec a \cdot \vec b = \left| {\vec a} \right|{\mkern 1mu} \cdot \left| {\vec b} \right|\).
Chọn A.
Câu 12 (TH):
Hướng dẫn:
Hàm số bậc hai \(y = a{x^2} + bx + c\) với a > 0 có bề lõm hướng lên và với a < 0 có bề lõm hướng xuống.
Giao với trục tung tại điểm nằm trên trục hoành thì c > 0 và nằm dưới trục hoành thì c < 0.
Đồ thị cắt trục hoành tại 2 điểm có hoành độ âm nên phương trình \(a{x^2} + bx + c = 0\) có 2 nghiệm âm.
Cách giải:
Đồ thị hàm số có bề lõm hướng lên nên a > 0 => Loại D.
Đồ thị cắt trục tung tại điểm nằm trên trục hoành nên c > 0.
Đồ thị cắt trục hoành tại 2 điểm có hoành độ âm nên phương trình \(a{x^2} + bx + c = 0\) có 2 nghiệm âm.
\( \Rightarrow \frac{{ – b}}{a} < 0 \Leftrightarrow {\rm{ \;}} – b 0\) => Loại A và B.
Chọn C.
Câu 13 (TH):
Hướng dẫn:
Với \(a > 0\), hàm số bậc hai đồng biến trên \(\left( {\frac{{ – b}}{{2a}}; + \infty } \right)\) và nghịch biến trên \(\left( { – \infty ;\frac{{ – b}}{{2a}}} \right)\)
Cách giải:
Đồ thị hàm số \(f\left( x \right) = {x^2} – 4x + 5\) có \({x_I} = \frac{{ – b}}{{2a}} = 2\) và có \(a = 1 > 0\)
Suy ra hàm số nghịch biến trên \(\left( { – \infty ;2} \right)\), đồng biến trên \(\left( {2; + \infty } \right)\).
Chọn D.
Câu 14 (TH):
Hướng dẫn:
Hàm số \(y = \sqrt {f(x)} \) xác định khi \(f\left( x \right) \ge 0.\)
Xét dấu hàm số \(f\left( x \right) = 5 – 4x – {x^2}\), để giải \(f\left( x \right) \ge 0.\)
Cách giải:
Hàm số xác định khi \(5{x^2} – 4x – 1 \ge 0\).
Ta có \(a = {\rm{ \;}} – 1 0.\) \(f\left( x \right)\) có hai nghiệm phân biệt \(x = 1;x = {\rm{ \;}} – 5.\)
Vậy \( – 5 \le x \le 1\).
Chọn A.
Câu 15 (TH):
Hướng dẫn:
Giải phương trình \(\sqrt A {\rm{\;}} = B \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{B \ge 0}\\{A = {B^2}}\end{array}} \right.\)
Cách giải:
\(\sqrt {2{x^2} – 2} = x + 1 \Leftrightarrow \left\{ \begin{array}{l}x + 1 \ge 0\\2{x^2} – 2 = {\left( {x + 1} \right)^2}\end{array} \right.\)
\( \Leftrightarrow \left\{ \begin{array}{l}x \ge – 1\\2{x^2} – 2 = {x^2} + 2x + 1\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}x \ge – 1\\{x^2} – 2x – 3 = 0\end{array} \right.\)
\( \Leftrightarrow \left\{ \begin{array}{l}x \ge – 1\\\left[ \begin{array}{l}x = 3\\x = – 1\end{array} \right.\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 3\\x = – 1\end{array} \right.\)
Khi đó \({x_1} + {x_2} = 3 + \left( { – 1} \right) = 2\).
Chọn B.
Câu 16 (TH):
Hướng dẫn:
– Kiểm tra đáp án A bằng cách xác định hướng và độ dài của hai vecto \(\overrightarrow {MB} ;{\mkern 1mu} {\mkern 1mu} \overrightarrow {MC} .\)
– Kiểm tra các đáp án B, C, D bằng cách tính độ dài đoạn thẳng AM.
Cách giải:
Tam giác đều ABC cạnh a, có độ dài đường trung tuyến AM là:
\(A{M^2} = \frac{{A{C^2} + A{B^2}}}{2} – \frac{{B{C^2}}}{4} = \frac{{{a^2} + {a^2}}}{2} – \frac{{{a^2}}}{4} = \frac{{3a}}{4}.\)
\( \Rightarrow AM = \frac{{\sqrt 3 a}}{2}\)\( \Rightarrow \overrightarrow {\left| {AM} \right|} {\rm{ \;}} = \frac{{\sqrt 3 a}}{2}.\)
Chọn D.
Câu 17 (TH):
Hướng dẫn:
Biến đổi \(\overrightarrow {MA} {\rm{ \;}} – \overrightarrow {MB} {\rm{ \;}} + \overrightarrow {MC} {\rm{ \;}} = \vec 0\) về hai vectơ bằng nhau.
Xác định vị trí điểm M dựa vào điều kiện vừa tìm được.
Cách giải:
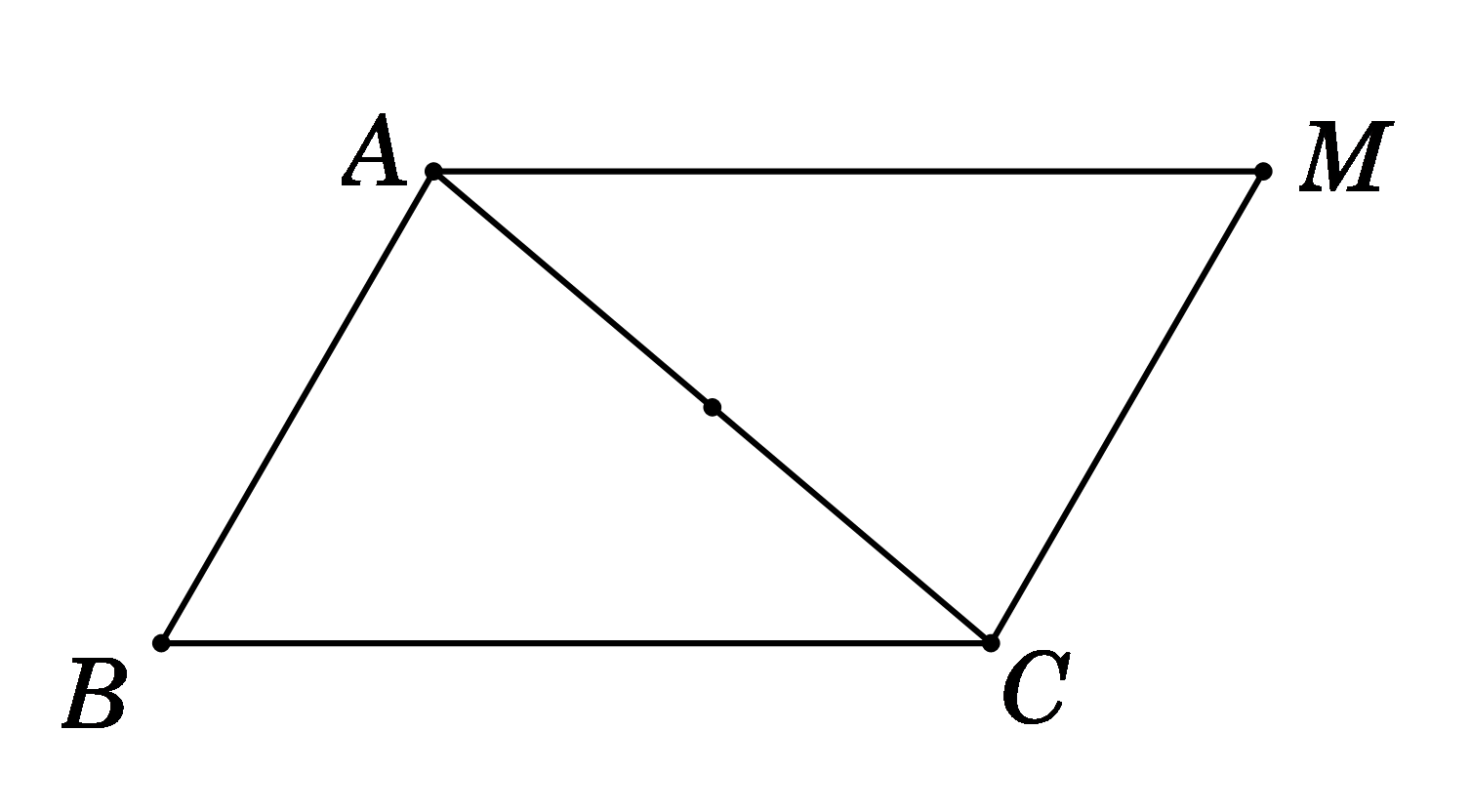
Ta có \(\overrightarrow {MA} {\rm{ \;}} – \overrightarrow {MB} {\rm{ \;}} + \overrightarrow {MC} {\rm{ \;}} = \vec 0\)\( \Leftrightarrow \overrightarrow {BA} {\rm{ \;}} + \overrightarrow {MC} {\rm{ \;}} = \vec 0{\rm{ \;}} \Leftrightarrow \overrightarrow {MC} {\rm{ \;}} = \overrightarrow {AB} \)
\( \Rightarrow \) MABC là hình bình hành.
Chọn A.
Câu 18 (TH):
Hướng dẫn:
Gọi M là trung điểm BC.
Sử dụng tính chất trung điểm.
Cách giải:
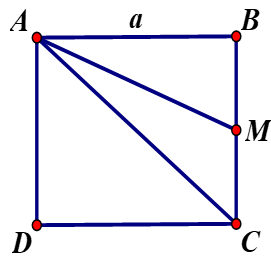
Gọi \(M\) là trung điểm BC.
Ta có: \(\left| {\overrightarrow {AB} {\rm{ \;}} + \overrightarrow {AC} } \right| = \left| {2\overrightarrow {AM} } \right| = 2AM = 2\sqrt {A{B^2} + B{M^2}} {\rm{ \;}} = 2\sqrt {{a^2} + {{\left( {\frac{a}{2}} \right)}^2}} {\rm{ \;}} = a\sqrt 5 \).
Chọn D.
Câu 19 (TH):
Hướng dẫn:
Áp dụng định nghĩa tích của vecto với một số, quy tắc cộng vecto để phân tích vecto.
Cách giải:

Ta có:
\(\overrightarrow {AD} {\rm{\;}} = \overrightarrow {AB} {\rm{\;}} + \overrightarrow {BD} {\rm{\;}} = \overrightarrow {AB} {\rm{\;}} + \frac{1}{3}\overrightarrow {BC} \)
\({\mkern 1mu} = \overrightarrow {AB} {\rm{\;}} + \frac{1}{3}\left( {\overrightarrow {BA} {\rm{\;}} + \overrightarrow {AC} } \right)\)\( = \overrightarrow {AB} {\rm{\;}} – \frac{1}{3}\overrightarrow {AB} {\rm{\;}} + \frac{1}{3}\overrightarrow {AC} \)\({\mkern 1mu} {\mkern 1mu} = \frac{2}{3}\overrightarrow {AB} {\rm{\;}} + \frac{1}{3}\overrightarrow {AC} \)
\( \Rightarrow \overrightarrow {AD} {\rm{\;}} = \frac{2}{3}\overrightarrow {AB} {\rm{\;}} + \frac{1}{3}\overrightarrow {AC} \)
Chọn A.
Câu 20 (TH):
Hướng dẫn:
Áp dụng:
+ \({\left( {\overrightarrow {AB} {\rm{\;}} – \overrightarrow {AC} } \right)^2} = A{B^2} + A{C^2} – 2\overrightarrow {AB} .\overrightarrow {AC} \) và quy tắc cộng vecto.
+ \(\cos A = \cos \left( {\overrightarrow {AB} ,{\mkern 1mu} {\mkern 1mu} \overrightarrow {AC} } \right) = \frac{{\overrightarrow {AB} .\overrightarrow {AC} }}{{\left| {\overrightarrow {AB} } \right|.\left| {\overrightarrow {AC} } \right|}}\)
Cách giải:
Tam giác ABC:\(AB = 2,\)\(BC = 4,{\mkern 1mu} {\mkern 1mu} CA = 3\).
Ta có: \({\left( {\overrightarrow {AB} {\rm{\;}} – \overrightarrow {AC} } \right)^2} = A{B^2} + A{C^2} – 2\overrightarrow {AB} .\overrightarrow {AC} \)
\( \Rightarrow \overrightarrow {AB} .\overrightarrow {AC} \)\( = \frac{{{{\overrightarrow {AB} }^2} + {{\overrightarrow {AC} }^2} – {{\left( {\overrightarrow {AB} {\rm{\;}} – \overrightarrow {AC} } \right)}^2}}}{2}\)\( = \frac{{{{\overrightarrow {AB} }^2} + {{\overrightarrow {AC} }^2} – {{\overrightarrow {BC} }^2}}}{2}\)\( = \frac{{A{B^2} + A{C^2} – B{C^2}}}{2}\)\( = \frac{{{2^2} + {3^2} – {4^2}}}{2} = \frac{{ – 3}}{2}\)
Lại có: \(\cos A = \frac{{\overrightarrow {AB} .\overrightarrow {AC} }}{{AB.AC}}\)\( = \frac{{ – \frac{3}{2}}}{{2.3}} = \frac{{ – 1}}{4}\)
Chọn B.
Câu 21 (VD):
Hướng dẫn:
Từ tọa độ đỉnh suy ra 2 phương trình, giải hệ tìm a, b.
Cách giải:
Vì S(-2;-1) là đỉnh của (P) nên \(\left\{ {\begin{array}{*{20}{l}}{\frac{{ – b}}{{2a}} = {\rm{ \;}} – 2}\\{ – 1 = 4a – 2b + 3}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{4a – b = 0}\\{4a – 2b = {\rm{ \;}} – 4}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{a = 1}\\{b = 4}\end{array}} \right.\).
Vậy 2a – b = 2.1 – 4 = -2.
Chọn A.
Câu 22 (VD):
Hướng dẫn:
\(f\left( x \right) = 0\) có nghiệm\( \Leftrightarrow \Delta {\rm{ \;}} \ge 0\)
Cách giải:
Xét \(f\left( x \right) = 0 \Leftrightarrow {x^2} – bx + 3 = 0\) \(\left( 1 \right)\)
Để tam thức bậc hai \(f\left( x \right)\) có nghiệm thì \(\left( 1 \right)\)có nghiệm \( \Leftrightarrow \Delta {\rm{ \;}} \ge 0\)\( \Leftrightarrow {b^2} – 12 \ge 0\)\( \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{b \ge 2\sqrt 3 }\\{b \le {\rm{ \;}} – 2\sqrt 3 }\end{array}} \right.\).
\( \Rightarrow b \in \left( { – {\mkern 1mu} \infty ;{\mkern 1mu} {\mkern 1mu} – {\mkern 1mu} 2\sqrt 3 } \right] \cup \left[ {2\sqrt 3 ;{\mkern 1mu} {\mkern 1mu} + {\mkern 1mu} \infty } \right)\)
Chọn C.
Câu 23 (VD):
Hướng dẫn:
Tìm các nghiệm của \(f\left( x \right)\), lập bảng xét dấu và kết luận.
Cách giải:
Giải: \(f\left( x \right) = 0 \Leftrightarrow 2{x^2} – 7x – 9 = 0\)\( \Leftrightarrow \left( {2x – 9} \right)\left( {x + 1} \right) = 0\)\( \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{x = {\rm{ \;}} – 1}\\{x = \frac{9}{2}}\end{array}} \right.\)

Dựa vào bảng xét dấu ta có: \(f\left( x \right) = 2{x^2} – 7x – 9 < 0\)\( \Leftrightarrow {\rm{ \;}} – 1 < x < \frac{9}{2}\)
Mà \(x \in \mathbb{Z} \Rightarrow x \in \left\{ {0;{\mkern 1mu} {\mkern 1mu} 1;{\mkern 1mu} {\mkern 1mu} 2;{\mkern 1mu} {\mkern 1mu} 3;{\mkern 1mu} {\mkern 1mu} 4} \right\}\)
Tổng tất cả các số nguyên \(x\) thỏa mãn là: \(0 + {\mkern 1mu} 1 + 2 + 3 + 4 = 10\)
Chọn D.
Câu 24 (VD):
Hướng dẫn:
Bước 1: Tìm tập xác định (\(\sqrt A \) xác định khi và chỉ khi \(A \ge 0\))
Bước 2: Giải phương trình bằng phương pháp bình phương 2 vế.
Cách giải:
\(\sqrt {5x – 1} {\rm{\;}} = \sqrt {3x – 2} {\rm{\;}} + \sqrt {x – 1} \)
TXĐ: \(D = \left[ {1; + \infty } \right]\)
\(\begin{array}{l}\sqrt {5x – 1} = \sqrt {3x – 2} + \sqrt {x – 1} \\ \Leftrightarrow {\left( {\sqrt {5x – 1} } \right)^2} = {\left( {\sqrt {3x – 2} + \sqrt {x – 1} } \right)^2}\\ \Leftrightarrow 5x – 1 = 3x – 2 + x – 1 + 2\sqrt {\left( {3x – 2} \right)\left( {x – 1} \right)} \\ \Leftrightarrow x + 2 = 2\sqrt {3{x^2} – 5x + 2} \end{array}\)
\( \Leftrightarrow \left\{ \begin{array}{l}x + 2 \ge 0\\{\left( {x + 2} \right)^2} = 4\left( {3{x^2} – 5x + 2} \right)\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}x \ge – 2\\{x^2} + 4x + 4 = 12{x^2} – 20x + 8\end{array} \right.\)
\( \Leftrightarrow \left\{ \begin{array}{l}x \ge – 2\\11{x^2} – 24x + 4 = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x \ge – 2\\\left[ \begin{array}{l}x = 2\\x = \frac{2}{{11}}\end{array} \right.\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 2\,\,\left( {Tm} \right)\\x = \frac{2}{{11}}\,\left( {ktm} \right)\end{array} \right.\)
Vậy phương trình có 1 nghiệm \(x = 2\)
Chọn C.
Câu 25 (VD):
Hướng dẫn:
– Vẽ hình, xác định các vectơ liên quan.
– Hình MNPQ là hình gì?
– Dựa vào tính chất hình MNPQ và MN là đường trung bình của tam ABC để chọn đáp án đúng.
Cách giải:
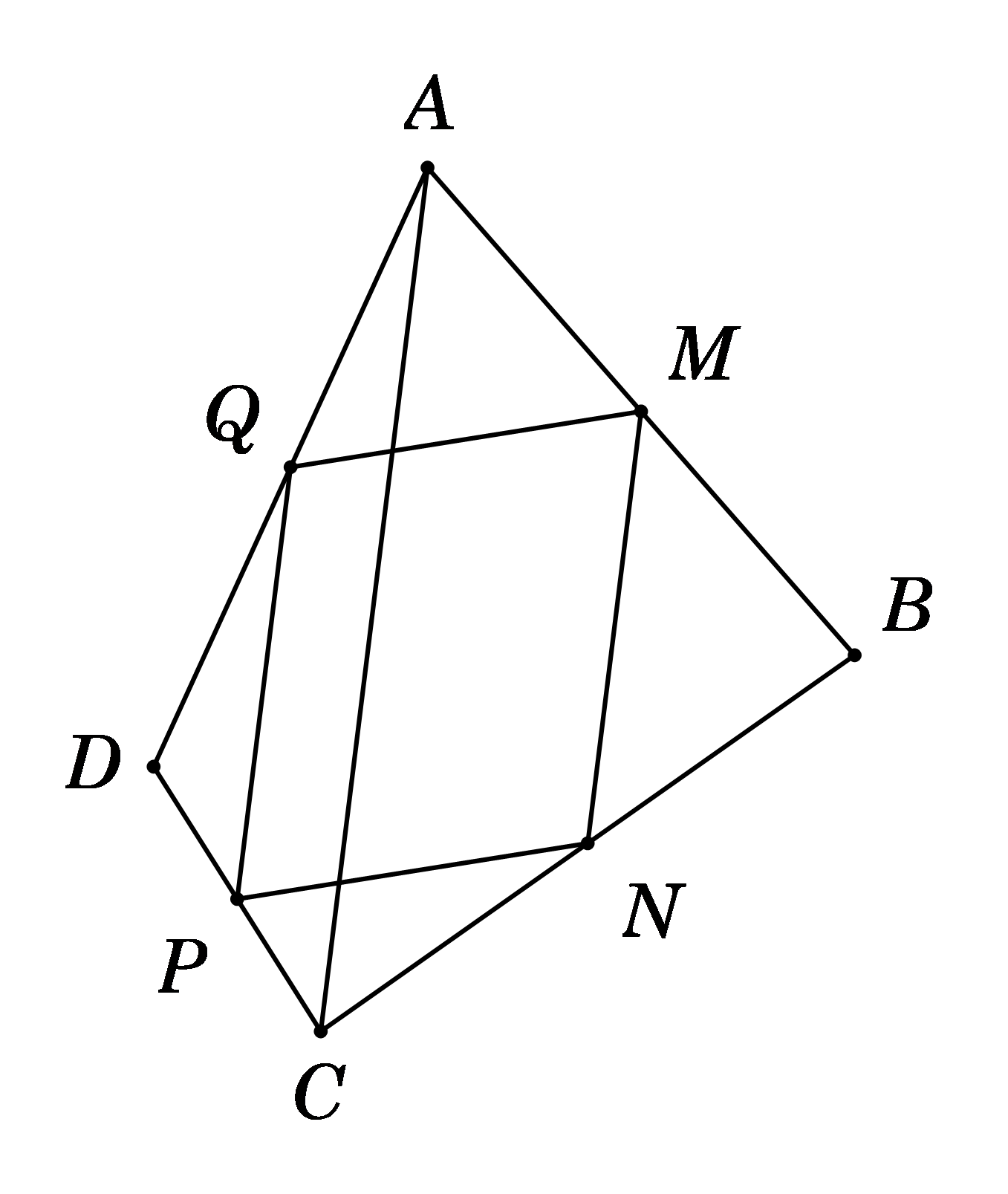
Ta có \(\left\{ {\begin{array}{*{20}{l}}{MN\parallel PQ}\\{MN = PQ}\end{array}} \right.\) (do cùng song song và bằng \(\frac{1}{2}AC\)).
Do đó MNPQ là hình bình hành.
Suy ra \(\overrightarrow {MN} {\rm{ \;}} = \overrightarrow {QP} \); \(\left| {\overrightarrow {QP} } \right| = \left| {\overrightarrow {MN} } \right|\); \(\overrightarrow {MQ} {\rm{ \;}} = \overrightarrow {NP} \).
Ta có: MN là đường trung bình tam giác ABC
Suy ra \(MN = \frac{1}{2}AC \Rightarrow \overrightarrow {MN} {\rm{ \;}} = \frac{1}{2}\overrightarrow {AC} \)
Chọn D.
Câu 26 (VD):
Hướng dẫn:
Biểu diễn \(\overrightarrow {MN} \) qua các vectơ \(\overrightarrow {MA} ,{\mkern 1mu} \overrightarrow {AD} ,{\mkern 1mu} {\mkern 1mu} \overrightarrow {DN} \).
Biểu diễn \(\overrightarrow {MN} \) qua các vectơ \(\overrightarrow {MB} ,{\mkern 1mu} \overrightarrow {BC} ,{\mkern 1mu} {\mkern 1mu} \overrightarrow {CN} \).
Cộng hai biểu thức trên và biểu diễn \(\overrightarrow {MN} \) qua \(\overrightarrow {AD} ,\overrightarrow {BC} .\)
Cách giải:
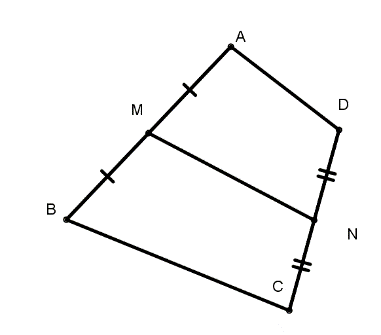
Ta có:
\(\overrightarrow {MN} {\rm{ \;}} = \overrightarrow {MA} {\rm{ \;}} + \overrightarrow {AD} {\rm{ \;}} + \overrightarrow {DN} \) (1)
\(\overrightarrow {MN} {\rm{ \;}} = \overrightarrow {MB} {\rm{ \;}} + \overrightarrow {BC} {\rm{ \;}} + \overrightarrow {CN} \) (2)
Cộng vế với vế của (1) và (2) ta được \(2\overrightarrow {MN} {\rm{ \;}} = \overrightarrow {AD} {\rm{ \;}} + \overrightarrow {BC} \) \( \Rightarrow \overrightarrow {MN} {\rm{ \;}} = \frac{1}{2}\left( {\overrightarrow {AD} {\rm{ \;}} + \overrightarrow {BC} } \right) \Rightarrow k = \frac{1}{2}\).
Chọn B.
Câu 27 (VD):
Hướng dẫn:
Áp dụng quy tắc cộng vecto, quy tắc hình bình hành để tìm vecto tổng.
Tính độ dài vecto vừa tìm được.
Cách giải:
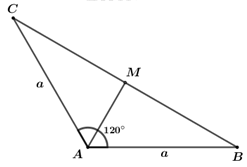
Ta có: \(\overrightarrow {AB} {\rm{\;}} + \overrightarrow {AC} {\rm{\;}} = 2\overrightarrow {AM} \)
\(\left| {\overrightarrow {AB} {\rm{\;}} + \overrightarrow {AC} } \right| = \left| {2\overrightarrow {AM} } \right| = 2\left| {\overrightarrow {AM} } \right| = 2.a.\cos {60^0} = a\)
Chọn B.
Câu 28 (VD):
Hướng dẫn:
Nếu \(M\) là trung điểm của cạnh BC thì \(\overrightarrow {AB} {\rm{\;}} + \overrightarrow {AC} {\rm{\;}} = 2\overrightarrow {AM} \).
Cách giải:
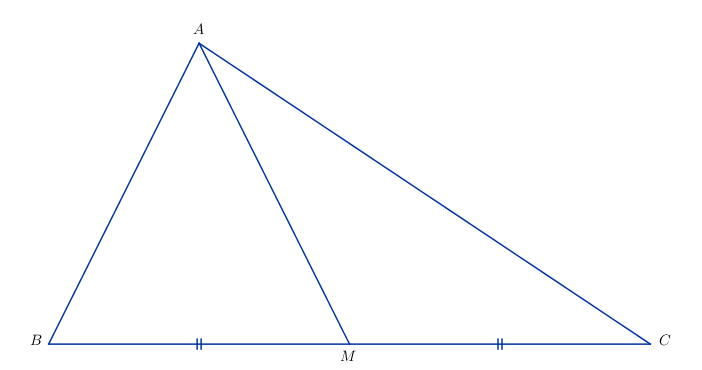
Vì \(M\) là trung điểm của BC nên \(\overrightarrow {AB} {\rm{\;}} + \overrightarrow {AC} {\rm{\;}} = 2\overrightarrow {AM} \)\( \Rightarrow \overrightarrow {AM} {\rm{\;}} = \frac{1}{2}\left( {\overrightarrow {AB} {\rm{\;}} + \overrightarrow {AC} } \right)\)
Ta có: \(\overrightarrow {AM} .\overrightarrow {BC} \)\( = \frac{1}{2}\left( {\overrightarrow {AB} {\rm{\;}} + \overrightarrow {AC} } \right).\overrightarrow {BC} \)\( = \frac{1}{2}\left( {\overrightarrow {AB} {\rm{\;}} + \overrightarrow {AC} } \right).\left( {\overrightarrow {AC} {\rm{\;}} – \overrightarrow {AB} } \right)\)
\( = \frac{1}{2}\left( {{{\overrightarrow {AC} }^2} – {{\overrightarrow {AB} }^2}} \right)\)\( = \frac{1}{2}\left( {A{C^2} – A{B^2}} \right)\)\( = \frac{{{b^2} – {c^2}}}{2}\)
Vậy \(\overrightarrow {AM} .\overrightarrow {BC} {\rm{\;}} = \frac{{{b^2} – {c^2}}}{2}\).
Chọn A.
Câu 29 (VDC):
Hướng dẫn:
Giải từng bất phương trình sau đó lấy giao các tập hợp nghiệm.
Cách giải:
\(\left\{ {\begin{array}{*{20}{l}}{{x^2} – 4x + 3 > 0}\\{3{x^2} – 10x + 3 \le 0}\\{4{x^2} – x – 3 > 0}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{x 3}\\{\frac{1}{3} \le x \le 3}\\{x 1}\end{array}} \right. \Leftrightarrow x \in \emptyset \)
Chọn A.
Câu 30 (VDC):
Hướng dẫn:
Giả sử \(\vec P{\rm{ \;}} = \overrightarrow {IA} \); \(\vec F{\rm{ \;}} = \overrightarrow {IB} \) có hợp lực \(\overrightarrow {{F_T}} {\rm{ \;}} = \overrightarrow {IC} \), lực căng dây \(\vec T{\rm{ \;}} = \overrightarrow {IN} \).
Đặt \(x > 0\) là cường độ lực \(\vec F\), \(x > 0\), đơn vị: \(N\).
Tính góc \(\angle ICB\), \(\angle CIA\).
Tính IC dựa và tam giác IAC vuông tại A.
Vì con lắc đứng yên nên \(IC = \left| {\overrightarrow {IC} } \right| = \left| {\vec T} \right|\).
Từ đó tìm x.
Cách giải:
Giả sử \(\vec P{\rm{ \;}} = \overrightarrow {IA} \); \(\vec F{\rm{ \;}} = \overrightarrow {IB} \) có hợp lực \(\overrightarrow {{F_T}} {\rm{ \;}} = \overrightarrow {IC} \), lực căng dây \(\vec T{\rm{ \;}} = \overrightarrow {IN} \).
Đặt \(x,x > 0\) là cường độ của lực \(\vec F\), đơn vị \(N\).
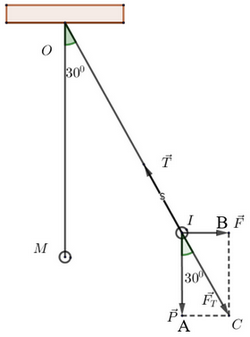
Dễ thấy \(\widehat {IOM} = \widehat {ICB}\) (so le trong) suy ra \(\widehat {ICB} = {30^^\circ }\).
Mà \(\widehat {ICB} = \widehat {CIA}\) nên \(\widehat {CIA} = {30^^\circ }\).
Ta có \(AC = IB = x \Rightarrow IC = \frac{{AC}}{{{\rm{sin3}}{0^^\circ }}} = 2x\).
Do con lắc đứng yên tại \(I\)nên lực căng dây \(\vec T\) có cùng cường độ với hợp lực \(\overrightarrow {{F_T}} \).
Nên \(2x = 30 \Leftrightarrow x = 15\).
Vậy cường độ của lực tác dụng \(\vec F\) bằng 15N.
Chọn C.
II. Phần tự luận
Câu 1 (TH):
Hướng dẫn:
a) Cho \(I\) là trung điểm của AB ta có: \(\overrightarrow {IA} {\rm{\;}} + \overrightarrow {IB} {\rm{\;}} = \vec 0.\)
b) Biểu diễn \(\overrightarrow {AS} \) theo vecto \(\overrightarrow {AI} \) rồi suy ra \(A,{\mkern 1mu} {\mkern 1mu} S,{\mkern 1mu} {\mkern 1mu} I\) thẳng hàng.
Cách giải:
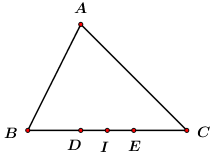
a) Chứng minh rằng: \(\overrightarrow {AB} {\rm{\;}} + \overrightarrow {AC} {\rm{\;}} = \overrightarrow {AD} {\rm{\;}} + \overrightarrow {AE} \)
Ta có: \(\overrightarrow {AB} {\rm{\;}} + \overrightarrow {AC} {\rm{\;}} = 2\overrightarrow {AI} \) (I là trung điểm của BC)
Vì \(BD = DE = EC,{\mkern 1mu} {\mkern 1mu} I\) là trung điểm BC
\( \Rightarrow I\) là trung điểm DE
\(\begin{array}{*{20}{l}}{ \Rightarrow \overrightarrow {AD} {\rm{\;}} + \overrightarrow {AE} {\rm{\;}} = 2\overrightarrow {AI} }\\{ \Rightarrow \overrightarrow {AB} {\rm{\;}} + \overrightarrow {AC} {\rm{\;}} = \overrightarrow {AD} {\rm{\;}} + \overrightarrow {AE} \;\left( { = 2\overrightarrow {AI} } \right)}\end{array}\)
b) Tính: \(\overrightarrow {AS} {\rm{\;}} = \overrightarrow {AB} {\rm{\;}} + \overrightarrow {AD} {\rm{\;}} + \overrightarrow {AC} {\rm{\;}} + \overrightarrow {AE} \) theo \(\overrightarrow {AI} .\) Từ đó suy ra \(A,{\mkern 1mu} {\mkern 1mu} S,{\mkern 1mu} {\mkern 1mu} I\) thẳng hàng.
\(\overrightarrow {AS} {\rm{\;}} = \overrightarrow {AB} {\rm{\;}} + \overrightarrow {AD} {\rm{\;}} + \overrightarrow {AC} {\rm{\;}} + \overrightarrow {AE} \)
\(\begin{array}{*{20}{l}}{ \Rightarrow \overrightarrow {AS} {\rm{\;}} = \left( {\overrightarrow {AB} {\rm{\;}} + \overrightarrow {AC} } \right) + \left( {\overrightarrow {AD} {\rm{\;}} + \overrightarrow {AE} } \right)}\\{ \Rightarrow \overrightarrow {AS} {\rm{\;}} = 2\overrightarrow {AI} {\rm{\;}} + 2\overrightarrow {AI} }\\{ \Rightarrow \overrightarrow {AS} {\rm{\;}} = 4\overrightarrow {AI} }\end{array}\)
\( \Rightarrow \) \(A,{\mkern 1mu} {\mkern 1mu} S,{\mkern 1mu} {\mkern 1mu} I\) thẳng hàng.
Câu 2 (VD):
Hướng dẫn:
– Gọi x đồng là số tiền mà doanh nghiệp A dự định giảm giá; \(0 \le x \le 4\).
– Lập phương trình tính lợi nhuận khi bán một chiếc xe.
– Tính số xe mà doanh nghiệp bán được trong một năm.
– Lập hàm số biểu thị lợi nhuận doanh nghiệp thu được trong một năm.
– Xét sự biến thiên hàm số trên \([0;4]\) và tìm giá trị lớn nhất của nó.
– Kết luận bài toán.
Cách giải:
Gọi x đồng là số tiền mà doanh nghiệp A dự định giảm giá; \(0 \le x \le 4\).
Khi đó:
Lợi nhuận thu được khi bán một chiếc xe là \(31 – x – 27 = 4 – x\) (đồng).
Số xe mà doanh nghiệp sẽ bán được trong một năm là: \(600 + 200x\) (chiếc).
Lợi nhuận mà doanh nghiệp thu được trong một năm là:
\(f\left( x \right) = \left( {4 – x} \right)\left( {600 + 200x} \right) = {\rm{ \;}} – 200{x^2} + 200x + 2400.\)
Xét hàm số \(f\left( x \right) = {\rm{ \;}} – 200{x^2} + 200x + 2400\) trên đoạn \([0;4]\) có bảng biến thiên sau:

Suy ra \(\mathop {\max }\limits_{[0;4]} f\left( x \right) = 2450 \Leftrightarrow x = \frac{1}{2}.\)
Vậy giá mới của chiếc xe là 30,5 triệu đồng thì lợi nhuận thu được là cao nhất.
Câu 3 (VDC):
Hướng dẫn:
Điều kiện tương đương là:
\(\left\{ {\begin{array}{*{20}{l}}{\Delta ‘ > 0}\\{{x_1} + {x_2} > 6}\\{\left( {{x_1} – 3} \right)\left( {{x_2} – 3} \right) > 0}\end{array}} \right.\)
Giải điều kiện dựa vào định lí Vi-ét.
Cách giải:
Phương trình có 2 nghiệm phân biệt \({x_1} > {x_2} > 3\).
Điều kiện để phương trình có hai nghiệm lớn hơn 3 là:
\(\left\{ {\begin{array}{*{20}{l}}{\Delta ‘ > 0}\\{{x_1} + {x_2} > 6}\\{\left( {{x_1} – 3} \right)\left( {{x_2} – 3} \right) > 0}\end{array}} \right.\)\( \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{2a – 2 > 0}\\{6a > 6}\\{{x_1}{x_2} – 3\left( {{x_1} + {x_2}} \right) + 9 > 0}\end{array}} \right.\)
\( \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{a > 1}\\{9{a^2} – 2a + 2 – 3.6a + 9 > 0}\end{array}} \right.\) \( \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{a > 1}\\{9{a^2} – 20a + 11 > 0}\end{array}} \right.\)
\( \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{a > 1}\\{\left[ {\begin{array}{*{20}{l}}{a > \frac{{11}}{9}}\\{a \frac{{11}}{9}\).
Do a nguyên và nhỏ nhất nên a = 2.