Đề thi giữa kì 2 Toán 10 Cánh diều – Đề số 2: Phần trắc nghiệm (7 điểm) Có bao nhiêu số tự nhiên từ 1 đến 20 không nguyên tố cùng nhau với số 15? A. 11 số. B. 10 số. C

Đề thi:

Phần trắc nghiệm (7 điểm)

Câu 1: Có bao nhiêu số tự nhiên từ 1 đến 20 không nguyên tố cùng nhau với số 15?

A. 11 số.

B. 10 số.

C. 9 số.

D. 8 số.

Câu 2: Khi chọn thực đơn để tổ chức tiệc sinh nhật, cô Yến yêu cầu nhà hàng chuẩn bị một món khai vị, một món chính và một món tráng miệng. Biết rằng nhà hàng có 3 loại món khai vị, 5 loại món chính và 2 loại món tráng miệng. Hỏi cô Yến có bao nhiêu cách chọn thực đơn cho bữa tiệc sinh nhật?

A. 10 cách.

B. 15 cách.

C. 25 cách.

D. 30 cách.

Câu 3: Mã mở khoá của một chiếc khoá số là một dãy gồm bốn chữ số. Mỗi chữ số có thể là một chữ số bất kì từ 0 đến 9. Hỏi có thể có bao nhiêu mã mở khoá khác nhau như vậy?

A. \({4^9}\)mã.

B. \({9^4}\) mã.

C. \({4^{10}}\) mã.

D. \({10^4}\) mã.

Câu 4: Trên giá sách có 5 quyển sách Ngũ văn khác nhau, 7 quyển sách Toán khác nhau và 6 quyển sách Tiếng Anh khác nhau. Hỏi có bao nhiêu cách chọn hai quyển sách khác môn?

A. 210 cách.

B. 107 cách.

C. 47 cách.

D. 72 cách.

Câu 5: Với \(k,n\) là các số tự nhiên và \(0 \le k \le n\), công thức nào sau đây là đúng?

A. \(C_n^k = \frac{{n!}}{{(n – k)!k!}}\).

B. \(C_n^k = \frac{{n!}}{{k!}}\).

C. \(C_n^k = \frac{{n!}}{{(n – k)!}}\).

D. \(C_n^k = \frac{{(n – k)!k!}}{{n!}}\).

Câu 6: Số cách chia 5 chiếc kẹo khác nhau cho 5 bạn nhỏ (mỗi bạn một chiếc kẹo) là:

A. 5! cách.

B. 10! cách.

C. 4! cách.

D. 16 cách.

Câu 7: Có bao nhiêu số có ba chữ số khác nhau đều là các chữ số lẻ?

A. 120 số.

B. 60 số.

C. 240 số.

D. 15 số.

Câu 8: Có bao nhiêu cách xếp 5 quyển sách Văn khác nhau và 7 quyển sách Toán khác nhau trên một kệ sách dài nếu các quyển sách Văn phải xếp kề nhau?

A. \(12!\).

B. \(2.5!.7!\).

C. \(8!.5!\).

D. \(5!.7!\).

Câu 9: Có 14 người gồm 8 nam và 6 nữ. Có bao nhiêu cách chọn một tổ 6 người trong đó có nhiều nhất 2 nữ?

A. 1524.

B. 472.

C. 1414.

D. 3003.

Câu 10: Tính số cách chọn ra một nhóm 5 người từ 20 người sao cho trong nhóm đó có 1 tổ trưởng, 1 tổ phó và 3 thành viên còn lại có vai trò như nhau.

A. 310080.

B. 930240.

C. 1860480.

D. 15505.

Câu 11: Có bao nhiêu cách để đi từ \(A\) đến \(C\) mà qua \(B\) trong hình sau đây?

A. 15 cách.

B. 20 cách.

C. 21 cách.

D. 24 cách.

Câu 12: Cuối buổi liên hoan trước khi ra về, mọi người đều bắt tay nhau, hai người bất kì chỉ bắt tay nhau một lần. Hỏi số người tham dự là bao nhiêu? Biết số cái bắt tay là 28.

A. \(14.\)

B. \(7.\)

C. 8.

D. 28.

Câu 13: Một tỉnh tổ chức giải bóng đá cho các trường THPT trong tỉnh. Có 20 đội tham gia thi đấu vòng tròn một lượt (hai đội bất kì gặp nhau 1 lần). Chi phí tối thiểu cho mỗi trận đấu (sân bãi, trọng tài, y tế,.) là 600000 đồng. Chi phí trao giải (tiền thưởng, loa đài,.) là 10 triệu đồng. Hỏi ban tổ chức phải chuẩn bị tối thiểu bao nhiêu tiền để tổ chức giải?

A. 122 triệu đồng.

B. 124 triệu đồng.

C. 120 triệu đồng.

D. 123 triệu đồng.

Câu 14: Có bao nhiêu cách xếp 10 học sinh gồm 5 học sinh nam và 5 học sinh nữ thành một hàng sao cho hai học sinh nữ bất kì không đứng cạnh nhau?

A. 3628800.

B. 86400.

C. 14400.

D. 120.

Câu 15: Khai triển của \({(x – 1)^4}\) là:

A. \({x^4} + 4{x^3} + 6{x^2} + 4x + 1\).

B. \({x^4} – 4{x^3} – 6{x^2} – 4x – 1\).

C. \({x^4} – 4{x^3} + 6{x^2} – 4x + 1\).

D. \({x^4} + 4{x^3} – 6{x^2} + 4x – 1\).

Câu 16: Hệ số tự do trong khai triển của \({(71x + 1)^4}\) là:

A. 71.

B. 70.

C. 4.

D. 1.

Câu 17: Trong các phát biểu sau, phát biểu nào sai?

A. \({(x – y)^4} = {y^4} – 4{x^3}y + 6{x^2}{y^2} – 4x{y^3} + {x^4}\).

B. \({(x + y)^4} = {x^4} + 4{x^3}y + 6{x^2}{y^2} + 4x{y^3} + {y^4}\).

C. \({(x – y)^4} = {x^4} – 4{x^3}y + 6{x^2}{y^2} + 4x{y^3} + {y^4}\).

D. \({(x + y)^4} = {\left[ {{{(x + y)}^2}} \right]^2}\).

Câu 18: Trong các phát biểu sau, phát biểu nào đúng?

A. \({(a + b)^5} = {a^5} + 5{a^4}b + 10{a^3}{b^2} + 10{a^2}{b^3} + 5a{b^4} + {b^5}\).

B. \({(a – b)^5} = {a^5} – 5{a^4}b – 10{a^3}{b^2} – 10{a^2}{b^3} – 5a{b^4} + {b^5}\).

C. \({(a + b)^5} = {a^5} + {b^5}\).

D. \({(a – b)^5} = {a^5} – {b^5}\).

Câu 19: Tìm hệ số của \({x^7}\) trong khai triển: \(f(x) = {\left( {{x^3} + \frac{2}{{{x^2}}}} \right)^n}\), với \(x > 0\), biết tổng ba hệ số đầu của \(x\) trong khai triển bằng 33.

A. 34.

B. 8.

C. 6.

D. 12.

Câu 20: Trong mặt phẳng toạ độ \(Oxy\), cho hình bình hành \(ABCD\) có \(A(4;1),B(1;3)\), \(C(5;5)\). Tọa độ điểm \(D\) là:

A. \((2;7)\).

B. \((8;3)\).

C. \((0; – 1)\).

D. \(( – 8; – 3)\).

Câu 21: Trong mặt phẳng toạ độ \(Oxy\), cho \(\vec a = 2\vec i – 3\vec j\) và \(\vec b = \vec i – \vec j\). Khẳng định nào dưới đây là đúng?

A. \(\vec a + \vec b = (2; – 3)\).

B. \(\vec a + \vec b = (1; – 1)\).

C. \(\vec a + \vec b = (3; – 4)\).

D. \(\vec a + \vec b = ( – 1; – 2)\).

Câu 22: Trong mặt phẳng toạ độ \(Oxy\), cho \(\vec a = (2;t),\vec b = (1; – 5)\) và \(\vec c = (7;t)\). Với giá trị nào của \(t\) dưới đây thì \(\vec c = 2\vec a + 3\vec b\)?

A. \(t = 5\).

B. \(t = 15\).

C. \(t = – 5\).

D. \(t = – \frac{5}{2}\).

Câu 23: Trong mặt phẳng toạ độ \(Oxy\), cho \(\vec a = ( – 4;2),\vec b = (2k; – k)\). Với giá trị nào của \(k\) dưới đây thì \(\vec a = \vec b\)?

A. \(k = – \frac{1}{2}\).

B. \(k = 2\).

C. \(k = – 2\).

D. Không tồn tại \(k\).

Câu 24: Trong mặt phẳng toạ độ \(Oxy\), cho \(\vec a = ( – m + 2n; – 1),\vec b = (5; – m – n)\). Với giá trị nào của \(m,n\) dưới đây thì \(\vec a = \vec b\)?

A. \(m = – 1,n = 2\).

B. \(m = 2,n = – 1\).

C. \(m = 2,n = 1\).

D. Không tồn tại \(m,n\).

Câu 25: Trong mặt phẳng toạ độ \(Oxy\), cho \(A(2; – 3),B( – 4;1)\) và \(C( – 1; – 1)\). Khẳng định nào dưới đây là đúng?

A. \(\overrightarrow {AB} = 2\overrightarrow {AC} \).

B. \(\overrightarrow {AB} = \frac{1}{2}\overrightarrow {AC} \).

C. \(\overrightarrow {AB} = – 2\overrightarrow {AC} \).

D. \(\overrightarrow {AB} = – \frac{1}{2}\overrightarrow {AC} \).

Câu 26: Trong mặt phẳng toạ độ \(Oxy\), cho \(A(2;3),B( – 2; – 1)\) và \(C(4;5)\). Khẳng định nào dưới đây là sai?

A. \(\overrightarrow {AB} + 2\overrightarrow {AC} = \vec 0\).

B. \(\overrightarrow {AB} = – 2\overrightarrow {AC} \).

C. \(\overrightarrow {AB} – 2\overrightarrow {AC} = \vec 0\).

D. \(\overrightarrow {BA} = – 2\overrightarrow {CA} \).

Câu 27: Trong mặt phẳng toạ độ \(Oxy\), cho \(\vec a = ( – 2;1),\vec b = (3; – 2)\) và \(\vec c = (0;1)\). Biểu thức biểu diễn vectơ \(\vec c\) qua hai vectơ \(\vec a\) và \(\vec b\) là:

A. \(\vec c = 3\vec a + 2\vec b\).

B. \(\vec c = – 3\vec a – 2\vec b\).

C. \(\vec c = – 3\vec a + 2\vec b\).

D. \(\vec c = 3\vec a – 2\vec b\).

Câu 28: Trong mặt phẳng toạ độ \(Oxy\), cho tam giác \(ABC\) có \(A( – 6; – 1),B(3;4)\) và trọng tâm \(G(1;1)\). Tọa độ điểm \(C\) là:

A. \((6;3)\).

B. \(( – 6;3)\).

C. \((6;0)\).

D. \(( – 6;0)\).

Câu 29: Phương trình của đường thẳng \(\Delta \) đi qua điểm \(M(5;4)\) và có vectơ pháp tuyến \(\vec n(11; – 12)\) là:

A. \(5x + 4y + 7 = 0\).

B. \(5x + 4y – 7 = 0\).

C. \(11x – 12y – 7 = 0\).

D. \(11x – 12y + 7 = 0\).

Câu 30: Phương trình của đường thẳng \(\Delta \) đi qua điểm \(M(5;4)\) và vuông góc với đường thẳng \(x – 2y + 5 = 0\) là:

A. \(x – 2y + 3 = 0\).

B. \(2x + y – 14 = 0\).

C. \(x + 2y – 13 = 0\).

D. \(2x + y = 0\).

Câu 31: Cho đường thẳng \(\Delta \) có phương trình tổng quát là \(x – 2y – 5 = 0\). Phương trình nào sau đây là phương trình tham số của \(\Delta \)?

A. \(\left\{ {\begin{array}{*{20}{c}}{x = 3 + 2t}\\{y = 4 – t}\end{array}} \right.\).

B. \(\left\{ {\begin{array}{*{20}{l}}{x = t}\\{y = 5 + 2t}\end{array}} \right.\).

C. \(\left\{ {\begin{array}{*{20}{l}}{x = 3 + 4t}\\{y = 1 – 2t}\end{array}} \right.\).

D. \(\left\{ {\begin{array}{*{20}{l}}{x = 5 + 2t}\\{y = t}\end{array}} \right.\).

Câu 32: Trong mặt phẳng toạ độ \(Oxy\), cho hai điểm \(A(5;4),B( – 1;0)\). Đường trung trực của đoạn thẳng \(AB\) có phương trình là:

A. \(x – 2y + 5 = 0\).

B. \(3x + 2y – 10 = 0\).

C. \(3x + 2y – 5 = 0\).

D. \(2x + 3y – 1 = 0\).

Câu 33: Góc giữa hai đường thẳng \({\Delta _1}:2x + 4y – 1 = 0\) và \({\Delta _2}:x – 3y + 1 = 0\) là:

A. \({0^0}\).

B. \({45^0}\).

C. \({60^0}\).

D. \({90^0}\).

Câu 34: Góc giữa hai đường thẳng \({\Delta _1}:\left\{ {\begin{array}{*{20}{l}}{x = 2 + \sqrt 3 t}\\{y = 1 – t}\end{array}} \right.\) và \({\Delta _2}:\left\{ {\begin{array}{*{20}{l}}{x = 1 + m}\\{y = 5 – \sqrt 3 m}\end{array}} \right.\) (với \(t,m\) là các tham số) là:

A. \({30^0}\).

B. \({60^0}\).

C. \({90^0}\).

D. \({150^0}\).

Câu 35: Trong mặt phẳng toạ độ \(Oxy\), cho điểm \(A(5;0)\) và đường thẳng \(\Delta :12x – 5y + 5 = 0\). Khoảng cách từ \(A\) đến đường thẳng \(\Delta \) là:

A. 2.

B. 8.

C. 5.

D. \(2\frac{1}{2}\)

Phần tự luận (3 điểm)

Bài 1. Tính số các số tự nhiên đôi một khác nhau có 6 chữ số tạo thành từ các chữ số \(0,1,2,3,4,5\) sao cho hai chữ số 3 và 4 đứng cạnh nhau.

Bài 2. Tìm tất cả nghiệm thực của phương trình \(A_x^{10} + A_x^9 = 9A_x^8\).

Bài 3. Cho các vectơ \(\vec a = (1; – 2),\vec b = ( – 2; – 6),\vec c = (m + n; – m – 4n)\).

a) Hai vectơ \(\vec a,\vec b\) có cùng phương không? Tìm góc tạo bởi hai vectơ \(\vec a,\vec b\).

b) Tìm hai số \(m,n\) sao cho \(\vec c\) cùng phương \(\vec a\) và \(|\vec c| = 3\sqrt 5 \).

Bài 4. Viết phương trình đường thẳng \(\Delta \) biết rằng:

a) \(\Delta \) chắn các trục tọa độ tại hai điểm \(A( – 4;0),B(0; – 2)\).

b) \(\Delta \) qua điểm \(E(2;3)\), đồng thời cắt các tia \(Ox,Oy\) tại các điểm \(M,N\) (khác gốc tọa độ \(O\)) biết rằng \(OM + ON\) bé nhất.

——– Hết ——–

Đáp án Đề thi:

Phần trắc nghiệm

Câu 1: Có bao nhiêu số tự nhiên từ 1 đến 20 không nguyên tố cùng nhau với số 15?

A. 11 số.

B. 10 số.

C. 9 số.

D. 8 số.

Lời giải

Đáp án C.

Câu 2: Khi chọn thực đơn để tổ chức tiệc sinh nhật, cô Yến yêu cầu nhà hàng chuẩn bị một món khai vị, một món chính và một món tráng miệng. Biết rằng nhà hàng có 3 loại món khai vị, 5 loại món chính và 2 loại món tráng miệng. Hỏi cô Yến có bao nhiêu cách chọn thực đơn cho bữa tiệc sinh nhật?

A. 10 cách.

B. 15 cách.

C. 25 cách.

D. 30 cách.

Lời giải

Đáp án D.

Câu 3: Mã mở khoá của một chiếc khoá số là một dãy gồm bốn chữ số. Mỗi chữ số có thể là một chữ số bất kì từ 0 đến 9. Hỏi có thể có bao nhiêu mã mở khoá khác nhau như vậy?

A. \({4^9}\)mã.

B. \({9^4}\) mã.

C. \({4^{10}}\) mã.

D. \({10^4}\) mã.

Lời giải

Đáp án D.

Câu 4: Trên giá sách có 5 quyển sách Ngũ văn khác nhau, 7 quyển sách Toán khác nhau và 6 quyển sách Tiếng Anh khác nhau. Hỏi có bao nhiêu cách chọn hai quyển sách khác môn?

A. 210 cách.

B. 107 cách.

C. 47 cách.

D. 72 cách.

Lời giải

Đáp án B.

Câu 5: Với \(k,n\) là các số tự nhiên và \(0 \le k \le n\), công thức nào sau đây là đúng?

A. \(C_n^k = \frac{{n!}}{{(n – k)!k!}}\).

B. \(C_n^k = \frac{{n!}}{{k!}}\).

C. \(C_n^k = \frac{{n!}}{{(n – k)!}}\).

D. \(C_n^k = \frac{{(n – k)!k!}}{{n!}}\).

Lời giải

Đáp án A.

Câu 6: Số cách chia 5 chiếc kẹo khác nhau cho 5 bạn nhỏ (mỗi bạn một chiếc kẹo) là:

A. 5! cách.

B. 10! cách.

C. 4! cách.

D. 16 cách.

Lời giải

Đáp án A.

Câu 7: Có bao nhiêu số có ba chữ số khác nhau đều là các chữ số lẻ?

A. 120 số.

B. 60 số.

C. 240 số.

D. 15 số.

Lời giải

Đáp án B.

Câu 8: Có bao nhiêu cách xếp 5 quyển sách Văn khác nhau và 7 quyển sách Toán khác nhau trên một kệ sách dài nếu các quyển sách Văn phải xếp kề nhau?

A. \(12!\).

B. \(2.5!.7!\).

C. \(8!.5!\).

D. \(5!.7!\).

Lời giải

Ta coi 5 quyển sách Văn là một Quyển và xếp Quyển này với 7 quyển sách Toán khác nhau ta có 8! cách xếp. Mỗi cách đổi vị trí các quyển sách văn cho nhau thì tương ứng sinh ra một cách xếp mới, mà có 5! cách đổi vị trí các quyển sách Văn. Vậy số cách xếp là \(8!.5\)!.

Đáp án C.

Câu 9: Có 14 người gồm 8 nam và 6 nữ. Có bao nhiêu cách chọn một tổ 6 người trong đó có nhiều nhất 2 nữ?

A. 1524.

B. 472.

C. 1414.

D. 3003.

Lời giải

Ta có các trường hợp sau:

+ Chọn 6 nam và không có nữ có: \(C_8^6 = 28\) (cách),

+ Chọn 1 nũ̃ và 5 nam: \(C_6^1C_8^5 = 336\) (cách),

+ Chọn 2 nữ 4 nam có: \(C_6^2C_8^4 = 1050\) (cách).

Theo quy tắc cộng có: \(28 + 336 + 1050 = 1414\) cách để chọn một tổ có 6 người trong đó có nhiều nhất 2 nữ.

Đáp án C.

Câu 10: Tính số cách chọn ra một nhóm 5 người từ 20 người sao cho trong nhóm đó có 1 tổ trưởng, 1 tổ phó và 3 thành viên còn lại có vai trò như nhau.

A. 310080.

B. 930240.

C. 1860480.

D. 15505.

Lời giải

Có 20 cách để chọn 1 tổ trưởng từ 20 người,

Sau khi chọn 1 tổ trưởng thì có 19 cách để chọn 1 tổ phó,

Sau đó có \(C_{18}^3\) cách để chọn 3 thành viên còn lại.

Vậy có \(20 \cdot 19 \cdot C_{18}^3 = 310080\) cách chọn một nhóm 5 người thỏa yêu cầu bài toán.

Đáp án A.

Câu 11: Có bao nhiêu cách để đi từ \(A\) đến \(C\) mà qua \(B\) trong hình sau đây?

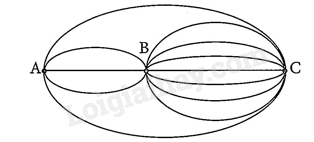
A. 15 cách.

B. 20 cách.

C. 21 cách.

D. 24 cách.

Lời giải

Đáp án C.

Câu 12: Cuối buổi liên hoan trước khi ra về, mọi người đều bắt tay nhau, hai người bất kì chỉ bắt tay nhau một lần. Hỏi số người tham dự là bao nhiêu? Biết số cái bắt tay là 28.

A. \(14.\)

B. \(7.\)

C. 8.

D. 28.

Lời giải

Gọi số người tham dự trong buổi liên hoan là \(n,(n \ge 2,n \in \mathbb{N})\).

Số cái bắt tay của \(n\) người là \(C_n^2\). Ta có \(C_n^2 = 28 \Leftrightarrow \frac{{n(n – 1)}}{2} = 28\)

\( \Leftrightarrow {n^2} – n – 56 = 0\). Suy ra \(n = – 7\) (loại); \(n = 8\) (thoả mãn).

Vậy số người tham dự trong buổi liên hoan là 8.

Đáp án C.

Câu 13: Một tỉnh tổ chức giải bóng đá cho các trường THPT trong tỉnh. Có 20 đội tham gia thi đấu vòng tròn một lượt (hai đội bất kì gặp nhau 1 lần). Chi phí tối thiểu cho mỗi trận đấu (sân bãi, trọng tài, y tế,.) là 600000 đồng. Chi phí trao giải (tiền thưởng, loa đài,.) là 10 triệu đồng. Hỏi ban tổ chức phải chuẩn bị tối thiểu bao nhiêu tiền để tổ chức giải?

A. 122 triệu đồng.

B. 124 triệu đồng.

C. 120 triệu đồng.

D. 123 triệu đồng.

Lời giải

Cứ hai đội bất kì thì được một trận đấu nên số trận đấu là: \(C_{20}^2 = 190\) trận.

Vậy chi phí tối thiểu ban tổ chức phải chuẩn bị là:

\(190 \cdot 600000 + 10000000 = 124000000\) (đồng).

Đáp án B.

Câu 14: Có bao nhiêu cách xếp 10 học sinh gồm 5 học sinh nam và 5 học sinh nữ thành một hàng sao cho hai học sinh nữ bất kì không đứng cạnh nhau?

A. 3628800.

B. 86400.

C. 14400.

D. 120.

Lời giải

Xếp 5 học sinh nam vào các vị trí: N1, N2, N3, N4, N5 (như hình dưới đây) thành một hàng có: \(5! = 120\).

Để các học sinh cùng giới không đứng cạnh nhau thì 5 học sinh nữ được xếp vào 6 vị trí còn trống, số cách xếp 5 học sinh nữ là: \(A_6^5 = 720\).

Vậy số cách xếp 10 học sinh thoả mãn yêu cầu bài toán là: \(120 \cdot 720 = 86400\) cách.

Đáp án B.

Câu 15: Khai triển của \({(x – 1)^4}\) là:

A. \({x^4} + 4{x^3} + 6{x^2} + 4x + 1\).

B. \({x^4} – 4{x^3} – 6{x^2} – 4x – 1\).

C. \({x^4} – 4{x^3} + 6{x^2} – 4x + 1\).

D. \({x^4} + 4{x^3} – 6{x^2} + 4x – 1\).

Lời giải

Đáp án C.

Câu 16: Hệ số tự do trong khai triển của \({(71x + 1)^4}\) là:

A. 71.

B. 70.

C. 4.

D. 1.

Lời giải

Đáp án D.

Câu 17: Trong các phát biểu sau, phát biểu nào sai?

A. \({(x – y)^4} = {y^4} – 4{x^3}y + 6{x^2}{y^2} – 4x{y^3} + {x^4}\).

B. \({(x + y)^4} = {x^4} + 4{x^3}y + 6{x^2}{y^2} + 4x{y^3} + {y^4}\).

C. \({(x – y)^4} = {x^4} – 4{x^3}y + 6{x^2}{y^2} + 4x{y^3} + {y^4}\).

D. \({(x + y)^4} = {\left[ {{{(x + y)}^2}} \right]^2}\).

Lời giải

Đáp án C.

Câu 18: Trong các phát biểu sau, phát biểu nào đúng?

A. \({(a + b)^5} = {a^5} + 5{a^4}b + 10{a^3}{b^2} + 10{a^2}{b^3} + 5a{b^4} + {b^5}\).

B. \({(a – b)^5} = {a^5} – 5{a^4}b – 10{a^3}{b^2} – 10{a^2}{b^3} – 5a{b^4} + {b^5}\).

C. \({(a + b)^5} = {a^5} + {b^5}\).

D. \({(a – b)^5} = {a^5} – {b^5}\).

Lời giải

Đáp án A.

Câu 19: Tìm hệ số của \({x^7}\) trong khai triển: \(f(x) = {\left( {{x^3} + \frac{2}{{{x^2}}}} \right)^n}\), với \(x > 0\), biết tổng ba hệ số đầu của \(x\) trong khai triển bằng 33.

A. 34.

B. 8.

C. 6.

D. 12.

Lời giải

\(C_n^0 + 2C_n^1 + 4C_n^2 = 33 \Rightarrow n = 4\); Số hạng tổng quát của khai triển \(f(x) = {\left( {{x^3} + \frac{2}{{{x^2}}}} \right)^4}\) là: \({T_{k + 1}} = C_4^k{\left( {{x^3}} \right)^{4 – k}}{\left( {\frac{2}{{{x^2}}}} \right)^k} = {2^k}C_4^k{x^{12 – 5k}}\).

Số hạng chứa \({x^7}\) trong khai triển ứng với số mũ của \(x\) là: \(12 – 5k = 7 \Leftrightarrow k = 1\).

Vậy hệ số của \({x^2}\) trong khai triển là: \({2^2}C_4^2 = 24\).

Đáp án B.

Câu 20: Trong mặt phẳng toạ độ \(Oxy\), cho hình bình hành \(ABCD\) có \(A(4;1),B(1;3)\), \(C(5;5)\). Tọa độ điểm \(D\) là:

A. \((2;7)\).

B. \((8;3)\).

C. \((0; – 1)\).

D. \(( – 8; – 3)\).

Lời giải

Giả sử \(D(a;b)\). Ta có: \(\overrightarrow {AB} = ( – 3;2)\) và \(\overrightarrow {DC} = (5 – a;5 – b)\).

Vì \(ABCD\) là hình bình hành nên \(\overrightarrow {AB} = \overrightarrow {DC} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{ – 3 = 5 – a}\\{2 = 5 – b}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{a = 8}\\{b = 3.{\rm{ }}}\end{array}} \right.} \right.\) Vậy \(D(8;3)\).

Đáp án B.

Câu 21: Trong mặt phẳng toạ độ \(Oxy\), cho \(\vec a = 2\vec i – 3\vec j\) và \(\vec b = \vec i – \vec j\). Khẳng định nào dưới đây là đúng?

A. \(\vec a + \vec b = (2; – 3)\).

B. \(\vec a + \vec b = (1; – 1)\).

C. \(\vec a + \vec b = (3; – 4)\).

D. \(\vec a + \vec b = ( – 1; – 2)\).

Lời giải

Ta có: \(\vec a = (2; – 3),\vec b = (1; – 1)\). Suy ra \(\vec a + \vec b = (3; – 4)\).

Đáp án D.

Câu 22: Trong mặt phẳng toạ độ \(Oxy\), cho \(\vec a = (2;t),\vec b = (1; – 5)\) và \(\vec c = (7;t)\). Với giá trị nào của \(t\) dưới đây thì \(\vec c = 2\vec a + 3\vec b\)?

A. \(t = 5\).

B. \(t = 15\).

C. \(t = – 5\).

D. \(t = – \frac{5}{2}\).

Lời giải

Ta có: \(2\vec a = (4;2t),3\vec b = (3; – 15)\) và \(\vec c = (7;t)\).

Khi đó \(\vec c = 2\vec a + 3\vec b \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{7 = 4 + 3}\\{t = 2t – 15}\end{array}} \right.\).

Suy ra \(t = 15\).

Đáp án B.

Câu 23: Trong mặt phẳng toạ độ \(Oxy\), cho \(\vec a = ( – 4;2),\vec b = (2k; – k)\). Với giá trị nào của \(k\) dưới đây thì \(\vec a = \vec b\)?

A. \(k = – \frac{1}{2}\).

B. \(k = 2\).

C. \(k = – 2\).

D. Không tồn tại \(k\).

Lời giải

Ta có: \(\vec a = \vec b \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{ – 4 = 2k}\\{2 = – k}\end{array}} \right.\)

Suy ra \(k = – 2\).

Đáp án C.

Câu 24: Trong mặt phẳng toạ độ \(Oxy\), cho \(\vec a = ( – m + 2n; – 1),\vec b = (5; – m – n)\). Với giá trị nào của \(m,n\) dưới đây thì \(\vec a = \vec b\)?

A. \(m = – 1,n = 2\).

B. \(m = 2,n = – 1\).

C. \(m = 2,n = 1\).

D. Không tồn tại \(m,n\).

Lời giải

Đáp án A.

Câu 25: Trong mặt phẳng toạ độ \(Oxy\), cho \(A(2; – 3),B( – 4;1)\) và \(C( – 1; – 1)\). Khẳng định nào dưới đây là đúng?

A. \(\overrightarrow {AB} = 2\overrightarrow {AC} \).

B. \(\overrightarrow {AB} = \frac{1}{2}\overrightarrow {AC} \).

C. \(\overrightarrow {AB} = – 2\overrightarrow {AC} \).

D. \(\overrightarrow {AB} = – \frac{1}{2}\overrightarrow {AC} \).

Lời giải

Ta có: \(\overrightarrow {AB} = ( – 6;4)\) và \(\overrightarrow {AC} = ( – 3;2)\). Suy ra \(\overrightarrow {AB} = 2\overrightarrow {AC} \).

Đáp án A.

Câu 26: Trong mặt phẳng toạ độ \(Oxy\), cho \(A(2;3),B( – 2; – 1)\) và \(C(4;5)\). Khẳng định nào dưới đây là sai?

A. \(\overrightarrow {AB} + 2\overrightarrow {AC} = \vec 0\).

B. \(\overrightarrow {AB} = – 2\overrightarrow {AC} \).

C. \(\overrightarrow {AB} – 2\overrightarrow {AC} = \vec 0\).

D. \(\overrightarrow {BA} = – 2\overrightarrow {CA} \).

Lời giải

Đáp án C.

Câu 27: Trong mặt phẳng toạ độ \(Oxy\), cho \(\vec a = ( – 2;1),\vec b = (3; – 2)\) và \(\vec c = (0;1)\). Biểu thức biểu diễn vectơ \(\vec c\) qua hai vectơ \(\vec a\) và \(\vec b\) là:

A. \(\vec c = 3\vec a + 2\vec b\).

B. \(\vec c = – 3\vec a – 2\vec b\).

C. \(\vec c = – 3\vec a + 2\vec b\).

D. \(\vec c = 3\vec a – 2\vec b\).

Lời giải

Giả sử \(\vec c = x\vec a + y\vec b\), ta có: \(\left\{ {\begin{array}{*{20}{l}}{0 = – 2x + 3y}\\{1 = x – 2y}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{x = – 3}\\{y = – 2}\end{array}} \right.} \right.\) Suy ra \(\vec c = – 3\vec a – 2\vec b\).

Đáp án B.

Câu 28: Trong mặt phẳng toạ độ \(Oxy\), cho tam giác \(ABC\) có \(A( – 6; – 1),B(3;4)\) và trọng tâm \(G(1;1)\). Tọa độ điểm \(C\) là:

A. \((6;3)\).

B. \(( – 6;3)\).

C. \((6;0)\).

D. \(( – 6;0)\).

Lời giải

Đáp án C.

Câu 29: Phương trình của đường thẳng \(\Delta \) đi qua điểm \(M(5;4)\) và có vectơ pháp tuyến \(\vec n(11; – 12)\) là:

A. \(5x + 4y + 7 = 0\).

B. \(5x + 4y – 7 = 0\).

C. \(11x – 12y – 7 = 0\).

D. \(11x – 12y + 7 = 0\).

Lời giải

Đáp án C.

Câu 30: Phương trình của đường thẳng \(\Delta \) đi qua điểm \(M(5;4)\) và vuông góc với đường thẳng \(x – 2y + 5 = 0\) là:

A. \(x – 2y + 3 = 0\).

B. \(2x + y – 14 = 0\).

C. \(x + 2y – 13 = 0\).

D. \(2x + y = 0\).

Lời giải

Đáp án B.

Câu 31: Cho đường thẳng \(\Delta \) có phương trình tổng quát là \(x – 2y – 5 = 0\). Phương trình nào sau đây là phương trình tham số của \(\Delta \)?

A. \(\left\{ {\begin{array}{*{20}{c}}{x = 3 + 2t}\\{y = 4 – t}\end{array}} \right.\).

B. \(\left\{ {\begin{array}{*{20}{l}}{x = t}\\{y = 5 + 2t}\end{array}} \right.\).

C. \(\left\{ {\begin{array}{*{20}{l}}{x = 3 + 4t}\\{y = 1 – 2t}\end{array}} \right.\).

D. \(\left\{ {\begin{array}{*{20}{l}}{x = 5 + 2t}\\{y = t}\end{array}} \right.\).

Lời giải

Đáp án D.

Câu 32: Trong mặt phẳng toạ độ \(Oxy\), cho hai điểm \(A(5;4),B( – 1;0)\). Đường trung trực của đoạn thẳng \(AB\) có phương trình là:

A. \(x – 2y + 5 = 0\).

B. \(3x + 2y – 10 = 0\).

C. \(3x + 2y – 5 = 0\).

D. \(2x + 3y – 1 = 0\).

Lời giải

Đáp án B.

Câu 33: Góc giữa hai đường thẳng \({\Delta _1}:2x + 4y – 1 = 0\) và \({\Delta _2}:x – 3y + 1 = 0\) là:

A. \({0^0}\).

B. \({45^0}\).

C. \({60^0}\).

D. \({90^0}\).

Lời giải

Đáp án B.

Câu 34: Góc giữa hai đường thẳng \({\Delta _1}:\left\{ {\begin{array}{*{20}{l}}{x = 2 + \sqrt 3 t}\\{y = 1 – t}\end{array}} \right.\) và \({\Delta _2}:\left\{ {\begin{array}{*{20}{l}}{x = 1 + m}\\{y = 5 – \sqrt 3 m}\end{array}} \right.\) (với \(t,m\) là các tham số) là:

A. \({30^0}\).

B. \({60^0}\).

C. \({90^0}\).

D. \({150^0}\).

Lời giải

Đáp án A.

Câu 35: Trong mặt phẳng toạ độ \(Oxy\), cho điểm \(A(5;0)\) và đường thẳng \(\Delta :12x – 5y + 5 = 0\). Khoảng cách từ \(A\) đến đường thẳng \(\Delta \) là:

A. 2.

B. 8.

C. 5.

D. \(2\frac{1}{2}\)

Lời giải

Đáp án C.

Phần tự luận (3 điểm)

Bài 1. Tính số các số tự nhiên đôi một khác nhau có 6 chữ số tạo thành từ các chữ số \(0,1,2,3,4,5\) sao cho hai chữ số 3 và 4 đứng cạnh nhau.

Lời giải

Xét số có hình thức \(\overline {{\bf{0bcdef}}} \).

Số cách hoán đổi vị trí hai chữ số 3,4 (cùng nhóm \(X\)) là 2.

Số cách hoán đổi vị trí của \(X\) với các chữ số \(1,2,5\) là: 4!

Vậy số các số được lập theo hình thức này là \(2.4! = 48\).

Xét số có hình thức \(\overline {abcdef} \) trong đó \(a\) được phép bằng 0.

Số cách hoán đổi vị trí của hai chữ số 3,4 (cùng nhóm \(X\)) là 2.

Số cách hoán đổi vị trí của \(X\) với các chữ số \(0,1,2,5\) là: 5!.

Số các số được lập theo hình thức này là \(2.5! = 240\).

Vậy số các số tự nhiên thỏa mãn đề bài là \(240 – 48 = 192\).

Bài 2. Tìm tất cả nghiệm thực của phương trình \(A_x^{10} + A_x^9 = 9A_x^8\).

Lời giải

Điều kiện: \(x \in \mathbb{N},x \ge 10\).

Ta có: \(A_x^{10} + A_x^9 = 9A_x^8 \Leftrightarrow \frac{{x!}}{{(x – 10)!}} + \frac{{x!}}{{(x – 9)!}} = 9 \cdot \frac{{x!}}{{(x – 8)!}}\)

\(\begin{array}{l} \Leftrightarrow \frac{1}{{(x – 10)!}} + \frac{1}{{(x – 9)!}} = 9 \cdot \frac{1}{{(x – 8)!}} \Leftrightarrow \frac{{(x – 8)!}}{{(x – 10)!}} + \frac{{(x – 8)!}}{{(x – 9)!}} = 9 \cdot \frac{{(x – 8)!}}{{(x – 8)!}}\\ \Leftrightarrow (x – 8)(x – 9) + (x – 8) = 9 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{x = 11}\\{x = 5}\end{array}} \right.{\rm{ ™}}{\rm{. }}\end{array}\)

Vậy tập nghiệm phương trình là \(S = \{ 5;11\} \).

Bài 3. Cho các vectơ \(\vec a = (1; – 2),\vec b = ( – 2; – 6),\vec c = (m + n; – m – 4n)\).

a) Hai vectơ \(\vec a,\vec b\) có cùng phương không? Tìm góc tạo bởi hai vectơ \(\vec a,\vec b\).

b) Tìm hai số \(m,n\) sao cho \(\vec c\) cùng phương \(\vec a\) và \(|\vec c| = 3\sqrt 5 \).

Lời giải

a) Ta có: \(\frac{1}{{ – 2}} \ne \frac{{ – 2}}{{ – 6}} \Rightarrow \vec a,\vec b\) không cùng phương.

Ta có: \(\cos (\vec a,\vec b) = \frac{{\vec a \cdot \vec b}}{{|\vec a| \cdot |\vec b|}} = \frac{{1( – 2) + ( – 2)( – 6)}}{{\sqrt {{1^2} + {{( – 2)}^2}} \cdot \sqrt {{{( – 2)}^2} + {{( – 6)}^2}} }} = \frac{{\sqrt 2 }}{2} \Rightarrow (\vec a,\vec b) = 45^\circ \).

b) \(\vec c\) cùng phương \(\vec a\) và \(|\vec c| = 3\sqrt 5 \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{\frac{{m + n}}{1} = \frac{{ – m – 4n}}{{ – 2}}}\\{\sqrt {{{(m + n)}^2} + {{( – m – 4n)}^2}} = 3\sqrt 5 }\end{array}} \right.\)

\(\begin{array}{l} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}\begin{array}{l} – 2m – 2n = – m – 4n\\{(m + n)^2} + {(m + 4n)^2} = 45\end{array}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}\begin{array}{l}m = 2n\\{(3n)^2} + {(6n)^2} = 45\end{array}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}\begin{array}{l}m = 2n\\{(3n)^2} + {(6n)^2} = 45\end{array}\end{array}} \right.} \right.} \right.\\ \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}\begin{array}{l}m = 2n\\45{n^2} = 45\end{array}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}\begin{array}{l}m = 2\\n = 1\end{array}\end{array} \vee \left\{ {\begin{array}{*{20}{l}}\begin{array}{l}m = – 2\\n = – 1\end{array}\end{array}.} \right.} \right.} \right.\end{array}\)

Bài 4. Viết phương trình đường thẳng \(\Delta \) biết rằng:

a) \(\Delta \) chắn các trục tọa độ tại hai điểm \(A( – 4;0),B(0; – 2)\).

b) \(\Delta \) qua điểm \(E(2;3)\), đồng thời cắt các tia \(Ox,Oy\) tại các điểm \(M,N\) (khác gốc tọa độ \(O\)) biết rằng \(OM + ON\) bé nhất.

Lời giải

a) \(\Delta \) có phương trình theo đoạn chắn là \(\frac{x}{{ – 4}} + \frac{y}{{ – 2}} = 1\) hay \(x + 2y + 4 = 0\).

b) Gọi \(M(m;0) = \Delta \cap Ox,N(0;n) = \Delta \cap Oy\) với \(m,n > 0\). Suy ra \(\left\{ {\begin{array}{*{20}{l}}{OM = m}\\{ON = n}\end{array}} \right.\).

Phương trình \(\Delta \) được viết theo đoạn chắn \(\frac{x}{m} + \frac{y}{n} = 1\). Vì \(E(2;3) \in \Delta \) nên \(\frac{2}{m} + \frac{3}{n} = 1 \Rightarrow \frac{2}{m} = \frac{{n – 3}}{n} \Rightarrow m = \frac{{2n}}{{n – 3}}\). Vì \(m,n > 0\) nên \(n – 3 > 0 \Rightarrow n > 3\).

Ta có: \(OM + ON = m + n = \frac{{2n}}{{n – 3}} + n = 2 + \frac{6}{{n – 3}} + n = 5 + \frac{6}{{n – 3}} + (n – 3)\).

Áp dụng bất đẳng thức AM-GM: \(\frac{6}{{n – 3}} + (n – 3) \ge 2\sqrt {\frac{6}{{n – 3}} \cdot (n – 3)} = 2\sqrt 6 \).

Suy ra: \(OM + ON = 5 + \frac{6}{{n – 3}} + (n – 3) \ge 5 + 2\sqrt 6 \).

Khi tổng \(OM + ON\) đạt giá trị nhỏ nhất (bằng \(5 + 2\sqrt 6 \)) thì dấu bằng của bất đẳng thức trên xảy ra: \(\frac{6}{{n – 3}} = n – 3 \Rightarrow {(n – 3)^2} = 6 \Rightarrow n = \sqrt 6 + 3(n > 3)\). Suy ra \(m = \frac{{2(\sqrt 6 + 3)}}{{(\sqrt 6 + 3) – 3}} = \frac{{2\sqrt 6 + 6}}{{\sqrt 6 }} = 2 + \sqrt 6 \).

Phương trình tổng quát \(\Delta :\frac{x}{{2 + \sqrt 6 }} + \frac{y}{{3 + \sqrt 6 }} = 1\) hay \(\frac{x}{{2 + \sqrt 6 }} + \frac{y}{{3 + \sqrt 6 }} – 1 = 0\).