Trang chủ Lớp 10 Toán lớp 10 Đề thi đề kiểm tra Toán lớp 10 - Cánh diều Đề kiểm tra học kì 2 Toán 10 – Đề số 4...

Đề kiểm tra học kì 2 Toán 10 – Đề số 4 – Cánh diều: Trắc nghiệm ( 7 điểm) Lớp 10;A có 21 bạn nam và 18 bạn nữ. Hỏi có bao nhiêu cách chọn một học sinh làm lớp trưởng? A. 168 cách

Gợi ý giải Đề kiểm tra học kì 2 Toán 10 – Đề số 4 – Cánh diều – Đề thi học kì 2 – Đề thi đề kiểm tra Toán lớp 10 Cánh diều. I. PHẦN TRẮC NGHIỆM ( 35 câu – 7,0 điểm )….

Đề thi:

Trắc nghiệm ( 7 điểm)

Câu 1. Lớp \(10\;A\) có 21 bạn nam và 18 bạn nữ. Hỏi có bao nhiêu cách chọn một học sinh làm lớp trưởng?

A. 168 cách. B. 29 cách. C. 39 cách. D. 158 cách.

Câu 2. Một quán ăn phục vụ 5 món ăn vặt và 2 loại nước uống. Hỏi bạn Mai có bao nhiêu cách để gọi một món ăn và một loại nước uống?

A. 5 cách. B. 7 cách. C. 10 cách. D. 3 cách.

Câu 3. Ví dụ nào sau đây là một ví dụ về hoán vị?

A. Số cách xếp hàng theo hàng dọc của 10 bạn.

B. Số cách chia 10 bạn vào hai nhóm.

C. Số cách chọn ra 4 bạn trong nhóm 10 bạn.

D. Số cách xếp hàng của 5 bạn trong nhóm 10 bạn.

Câu 4. Đội tuyển toán có 5 bạn nam và 7 bạn nữ. Giáo viên phải chọn ra một nhóm bốn bạn. Hỏi giáo viên có bao nhiêu cách chọn?

A. \(\frac{{12!}}{{4!}}\). B. 12!. C. \(C_{12}^4\). D. \(A_{12}^4\).

Câu 5. Cho tập hợp \(A = \{ 1;2;3;4;5;6;7\} \). Hỏi có bao nhiêu cách lập được số có ba chữ số khác nhau từ các chữ số thuộc tập hợp \(A\)?

A. \(C_7^3\). B. \(C_7^4\). C. \(A_7^3\). D. \(A_7^4\).

Câu 6. Số cách chia 10 học sinh thành ba nhóm lần lượt có \(2,3,5\) học sinh là:

A. \(C_{10}^2 + C_{10}^3 + C_{10}^5\).

B. \(C_{10}^2 \cdot C_8^3 \cdot C_5^5\).

C. \(C_{10}^2 + C_8^3 + C_5^5\).

D. \(C_{10}^5 + C_5^3 + C_2^2\).

Câu 7. Có bao nhiêu cách xếp 5 sách Văn khác nhau và 7 sách Toán khác nhau trên một kệ sách dài nếu các sách Văn phải xếp kề nhau?

A. 5!.7!. B. \(2.5!.7!\). C. \(5!.8!\). D. \(12!\).

Câu 8. Giả sử ta dùng 5 màu để tô cho 3 nước khác nhau trên bản đồ và không có màu nào được dùng hai lần. Số các cách để chọn những màu cần dùng là:

A. \(\frac{{5!}}{{2!}}\).

B. 8.

C. \(\frac{{5!}}{{3!2!}}\).

D. \({5^3}\).

Câu 9. Khai triển của \({(x + 1)^4}\) là:

A. \({x^4} + 2{x^2} + 1\).

B. \({x^4} + 4{x^3} + 6{x^2} + 4x + 1\).

C. \({x^4} + 5{x^3} + 10{x^2} + 5x + 1\).

D. \({x^4} + 3{x^3} + 4{x^2} + 3x + 1\).

Câu 10. Hệ số của \({x^3}\) trong khai triển của \({(2x + 1)^4}\) là:

A. 4. B. 6. C. 10. D. 32.

Câu 11. Giả sử có khai triển \({(1 – 2x)^n} = {a_0} + {a_1}x + {a_2}{x^2} + \ldots + {a_n}{x^n}\). Tìm \({a_4}\) biết \({a_0} + {a_1} + {a_2} = 31\).

A. 80. B. \( – 80\). C. 40. D. \( – 40\).

Câu 12. Hình chữ nhật có các cạnh:\(x = 2m \pm 1cm\), \(y = 5m \pm 2cm\). Diện tích hình chữ nhật và sai số tuyệt đối của giá trị đó là:

A. \(10{m^2}\) và \(900c{m^2}\).

B. \(10{m^2}\) và \(500c{m^2}\).

C. \(10{m^2}\) và \(400c{m^2}\).

D. \(10{m^2}\) và \(1404\;c{m^2}\).

Câu 13. Một hình chữ nhật có diện tích là \(S = 108,57c{m^2} \pm 0,06c{m^2}.\) Số các chữ số chắc của \(S\)là:

A. \(5.\) B. \(4.\) C. \(3.\) D. \(2.\)

Câu 14. Cho tam giác \(ABC\) có độ dài ba cạnh đo được như sau \(a = 12\,{\rm{cm}} \pm 0,2\,{\rm{cm}}\); \(b = 10,2\,{\rm{cm}} \pm 0,2\,{\rm{cm}}\); \(c = 8\,{\rm{cm}} \pm 0,1\,{\rm{cm}}\). Tính chu vi \(P\) của tam giác và đánh giá sai số tuyệt đối, sai số tương đối của số gần đúng của chu vi qua phép đo.

A. \(1,6\% \) B. \(1,7\% \) C. \(1,662\% \) D. \(1,66\% \)

Câu 15. Số áo bán được trong một quý ở cửa hàng bán áo sơ mi nam được thống kê như sau:

Cỡ áo

Tần số

(Số áo bán được)

126

125

110

Giá trị mốt của bảng phân bố tần số trên bằng

A. \(38\). B. \(126\). C. \(42\). D. \(12\).

Câu 16. Tiền lương hàng tháng của \(7\) nhân viên trong một công ty du lịch lần lượt là:\(6,5\); \(8,4\); \(6,9\); \(7,2\); \(2,5\); \(6,7\); \(3,0\) (đơn vị: triệu đồng). Số trung vị của dãy số liệu thống kê trên bằng

A. \(6,7\) triệu đồng.

B. \(7,2\) triệu đồng.

C. \(6,8\) triệu đồng.

D. \(6,9\) triệu đồng.

Câu 17. Cho phương sai của các số liệu bằng \(4\). Tìm độ lệch chuẩn.

A. \(4\). B. \(2\). C. \(16\). D. \(8\).

Câu 18. Độ lệch chuẩn là

A. Căn bậc hai của phương sai.

B. Bình phương của phương sai.

C. Một nửa của phương sai.

D. Không phải các công thức trên.

Câu 19. Có 100 học sinh tham dự kì thi học sinh giỏi Toán (thang điểm 20). Kết quả cho trong bảng sau:

Khi đó độ lệch chuẩn là

A. \(1,98\). B. \(3,96\). C. \(15,23\) D. \(1,99\).

Câu 20. Điểm thi của lớp 10C của một trường Trung học Phổ Thông được trình bày ở bảng phân bố tần số sau:

Phương sai của bảng phân bố tần số đã cho là:

A. \(0,94\) B. \(3,94.\) C. \(2,94.\) D. \(1,94.\)

Câu 21. Điểm thi môn Toán lớp 10A₂ của một Trường trung học phổ thông được trình bày ở bảng phân bố tần số sau

Điểm thi	\(5\)	\(6\)	\(7\)	\(8\)	\(9\)	\(10\)
Tần số	\(7\)	\(5\)	\(10\)	\(12\)	\(4\)	\(2\)	\(n = 40\)

Trong các giá trị dưới đây, giá trị nào gần nhất với phương sai của bảng phân bố tần số trên?

A. \(0,94\). B. \(3,94\). C. \(2,94\). D. \(1,94\).

Câu 22. Gieo một đồng xu cân đối và đồng chất liên tiếp ba lần. Gọi \(A\) là biến cố “Có ít nhất hai mặt sấp xuất hiện liên tiếp” và \(B\) là biến cố “Kết quả ba lần gieo là như nhau”. Xác định biến cố \(A \cup B.\)

A. \(A \cup B = \left\{ {SSS,\,SSN,\,NSS,\,SNS,\,NNN} \right\}\)

B. \(A \cup B = \left\{ {SSS,\,NNN} \right\}\).

C. \(A \cup B = \left\{ {SSS,\,SSN,\,NSS,\,NNN} \right\}\)

D. \(A \cup B = \Omega \).

Câu 23. Gieo ngẫu nhiên một đồng tiền cân đối và đồng chất \(5\) lần. Tính số phần tử không gian mẫu.

A. \(64\). B. \(10\). C. \(32\). D. \(16\).

Câu 24. Gieo một con súc sắc. Xác suất để mặt \(6\) chấm xuất hiện.

A. \(\frac{1}{6}\). B. \(\frac{5}{6}\). C. \(\frac{1}{2}\). D. \(\frac{1}{3}\).

Câu 25. Gieo một con súc sắc cân đối và đồng chất 2 lần. Tính xác suất để tổng số chấm trong hai lần gieo nhỏ hơn 6.

A. \(\frac{2}{9}\).

B. \(\frac{{11}}{{36}}\).

C. \(\frac{1}{6}\).

D. \(\frac{5}{{18}}\).

Câu 26. Trong hệ trục \(Oxy,\) cho Elip \(\left( E \right)\) có các tiêu điểm \({F_1}\left( { – 4;0} \right),{F_2}\left( {4;0} \right)\) và một điểm \(M\) nằm trên \(\left( E \right)\). Biết rằng chu vi của tam giác \(M{F_1}{F_2}\) bằng 18. Xác định tâm sai e của \(\left( E \right).\)

A. \(e = \frac{4}{5}\).

B. \(e = \frac{4}{{18}}\).

C. \(e = – \frac{4}{5}\).

D. \(e = \frac{4}{9}\).

Câu 27. Trong mặt phẳng toạ độ \(Oxy\), cho \(\vec a = (1;2),\vec b = (3; – 3)\). Toạ độ của vectơ \(\vec c = 3\vec a – 2\vec b\) là:

A. \(( – 3;12)\).

B. \((3;12)\).

C. \((9;0)\).

D. \(( – 3;0)\).

Câu 28. Trong mặt phẳng toạ độ \(Oxy\), cho ba điểm \(A( – 1;2),B(2; – 2),C(3;1)\). Toạ độ của vectơ \(\overrightarrow {AB} + \overrightarrow {BC} \) là:

A. \(( – 4; – 1)\). B. \((4; – 1)\). C. \(( – 4;1)\). D. \((4;1)\).

Câu 29. Một đường thẳng có bao nhiêu vectơ pháp tuyến?

A. 0. B. 1. C. 2. D. Vô số.

Câu 30. Phương trình tổng quát của đường thẳng \(\Delta \) đi qua điểm \(M\left( {{x_0};{y_0}} \right)\) và có vectơ pháp tuyến \(\vec n(a;b)\) là:

A. \(\frac{{x – {x_0}}}{a} = \frac{{y – {y_0}}}{b}\).

B. \(b\left( {x – {x_0}} \right) – a\left( {y – {y_0}} \right) = 0\).

C. \(a\left( {x + {x_0}} \right) + b\left( {y + {y_0}} \right) = 0\).

D. \(a\left( {x – {x_0}} \right) + b\left( {y – {y_0}} \right) = 0\).

Câu 31. Đường Hyperbol \(\frac{{{x^2}}}{{16}} – \frac{{{y^2}}}{9} = 1\) có một tiêu điểm là điểm nào dưới đây ?

A.\(\left( { – 5;0} \right)\).

B.\(\left( {0;\sqrt 7 } \right)\).

C. \(\left( {\sqrt 7 ;0} \right)\).

D. \(\left( {0;5} \right)\).

Câu 32. Đường elip \(\frac{{{x^2}}}{{16}} + \frac{{{y^2}}}{7} = 1\) có tiêu cự bằng

A. \(3\). B. \(9\). C. \(6\). D. \(18\).

Câu 33. Trong mặt phẳng \(Oxy\), phương trình nào sau đây là phương trình của đường tròn?

A. \({x^2} + 2{y^2} – 4x – 8y + 1 = 0\).

B. \({x^2} + {y^2} – 4x + 6y – 12 = 0\).

C. \({x^2} + {y^2} – 2x – 8y + 20 = 0\).

D. \(4{x^2} + {y^2} – 10x – 6y – 2 = 0\).

Câu 34. Trong mặt phẳng \(Oxy\), đường tròn \(\left( C \right):{x^2} + {y^2} + 4x + 6y – 12 = 0\) có tâm là.

A. \(I\left( { – 2; – 3} \right)\). B. \(I\left( {2;3} \right)\). C. \(I\left( {4;6} \right)\). D. \(I\left( { – 4; – 6} \right)\).

Câu 35. Đường tròn \(\left( C \right)\) đi qua hai điểm \(A\left( {1;1} \right)\), \(B\left( {5;3} \right)\) và có tâm \(I\) thuộc trục hoành có phương trình là

A. \({\left( {x + 4} \right)^2} + {y^2} = 10\).

B. \({\left( {x – 4} \right)^2} + {y^2} = 10\).

C. \({\left( {x – 4} \right)^2} + {y^2} = \sqrt {10} \).

D. \({\left( {x + 4} \right)^2} + {y^2} = \sqrt {10} \).

Tự luận (3 điểm)

Câu 1. Từ một nhóm 30 học sinh lớp 12 gồm 15 học sinh khối \(A,10\) học sinh khối \(B\) và 5 học sinh khối \(C\), cần chọn ra 15 học sinh, hỏi có bao nhiêu cách chọn sao cho:

a) Số học sinh mỗi khối là bằng nhau?

b) Có ít nhất 5 học sinh khối \(A\) và có đúng 2 học sinh khối \(C\)?

Câu 2. Cho biểu thức \(Q = {(xy – 1)^5}\).

a) Viết khai triển biểu thức \(Q\) bằng nhị thức Newton.

b) Tìm số hạng có chứa \({x^2}{y^2}\) trong khai triển trên.

Câu 3. Người ta tiến hành phỏng vấn một số người về chất lượng của một loại sản phẩm mới. người điều tra yêu cầu cho điểm sản phẩm ( thang điểm 100) kết quả như sau:

80 65 51 48 45 61 30 35 84 83 60 58 75

72 68 39 41 54 61 72 75 72 61 58 65

a) Tìm phương sai và độ lệch chuẩn. Nhận xét gì về các kết quả nhận được.

b) Tìm khoảng biến thiên, khoảng tứ phân vị

c) Tìm giá trị bất thường

Câu 4. Cho tam giác \(ABC\) với \(A( – 1; – 2)\) và phương trình đường thẳng chứa cạnh \(BC\) là \(x – y + 4 = 0\).

a) Viết phương trình đường cao \(AH\) của tam giác.

b) Viết phương trình đường trung bình ứng với cạnh đáy \(BC\) của tam giác.

Đáp án Đề thi:

HƯỚNG DẪN GIẢI CHI TIẾT

THỰC HIỆN: BAN CHYÊN MÔN GiaiBaitapsgk.COM

I. PHẦN TRẮC NGHIỆM (35 câu – 7,0 điểm).

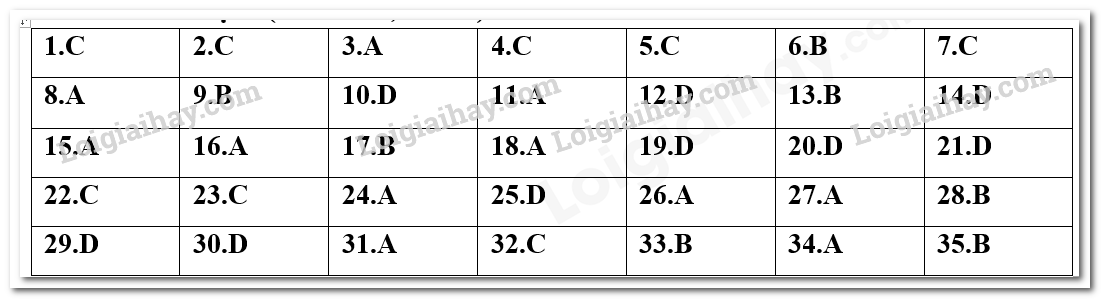
Câu 1. Lớp \(10\;A\) có 21 bạn nam và 18 bạn nữ. Hỏi có bao nhiêu cách chọn một học sinh làm lớp trưởng?

A. 168 cách. B. 29 cách. C. 39 cách. D. 158 cách.

Phương pháp

Áp dụng quy tắc cộng

Lời giải

Chọn C.

Áp dụng quy tắc cộng số cách chọn một học sinh làm lớp trưởng là \(21 + 18 = 39\)

Câu 2. Một quán ăn phục vụ 5 món ăn vặt và 2 loại nước uống. Hỏi bạn Mai có bao nhiêu cách để gọi một món ăn và một loại nước uống?

A. 5 cách. B. 7 cách. C. 10 cách. D. 3 cách.

Phương pháp

Áp dụng quy tắc nhân

Lời giải

Chọn C.

Áp dụng quy tắc nhân số cách để gọi một món ăn và một loại nước uống là \(21 + 18 = 39\)

Câu 3. Ví dụ nào sau đây là một ví dụ về hoán vị?

A. Số cách xếp hàng theo hàng dọc của 10 bạn.

B. Số cách chia 10 bạn vào hai nhóm.

C. Số cách chọn ra 4 bạn trong nhóm 10 bạn.

D. Số cách xếp hàng của 5 bạn trong nhóm 10 bạn.

Phương pháp

Áp dụng công thức hoán vị

Lời giải

Chọn A.

Câu 4. Đội tuyển toán có 5 bạn nam và 7 bạn nữ. Giáo viên phải chọn ra một nhóm bốn bạn. Hỏi giáo viên có bao nhiêu cách chọn?

A. \(\frac{{12!}}{{4!}}\). B. 12!. C. \(C_{12}^4\). D. \(A_{12}^4\).

Phương pháp

Áp dụng công thức tổ hợp

Lời giải

Chọn C.

Số học sinh ở đội tuyển toán là \(5 + 7 = 12\)

Vậy giáo viên có \(C_{12}^4\) cách chọn.

Câu 5. Cho tập hợp \(A = \{ 1;2;3;4;5;6;7\} \). Hỏi có bao nhiêu cách lập được số có ba chữ số khác nhau từ các chữ số thuộc tập hợp \(A\)?

A. \(C_7^3\). B. \(C_7^4\). C. \(A_7^3\). D. \(A_7^4\).

Phương pháp

Áp dụng công thức chỉnh hợp

Lời giải

Chọn C.

Số cách lập được số có ba chữ số khác nhau từ các chữ số thuộc tập hợp là \(A_7^3\)

Câu 6. Số cách chia 10 học sinh thành ba nhóm lần lượt có \(2,3,5\) học sinh là:

A. \(C_{10}^2 + C_{10}^3 + C_{10}^5\). B. \(C_{10}^2 \cdot C_8^3 \cdot C_5^5\).

C. \(C_{10}^2 + C_8^3 + C_5^5\). D. \(C_{10}^5 + C_5^3 + C_2^2\).

Phương pháp

Áp dụng công thức tổ hợp

Lời giải

Chọn \(B\).

Chọn 2 trong 10 học sinh vào nhóm thứ nhất: có \(C_{10}^2\) cách.

Chọn 3 trong 8 học sinh còn lại vào nhóm thứ hai: có \(C_8^3\) cách.

Chọn 5 trong 5 học sinh cuối cùng vào nhóm thứ ba: có \(C_5^5\) cách.

Vậy có \(C_{10}^2 \cdot C_8^3 \cdot C_5^5\) cách chọn thỏa mãn đề bài.

Câu 7. Có bao nhiêu cách xếp 5 sách Văn khác nhau và 7 sách Toán khác nhau trên một kệ sách dài nếu các sách Văn phải xếp kề nhau?

A. 5!.7!.

B. \(2.5!.7!\).

C. \(5!.8!\).

D. \(12!\).

Phương pháp

Áp dụng công thức hoán vị

Lời giải

Chọn C

Sắp xếp 5 quyển Văn chung một nhóm ngang (nhóm \(V)\): có 5! cách.

Sắp xếp 7 quyển Toán với \(V\) (ta xem như sắp xếp 8 phần tử): có \(8!\) cách. Vậy có tất cả \(5!.8!\) cách sắp xếp thỏa mãn đề bài.

A. \(\frac{{5!}}{{2!}}\). B. 8. C. \(\frac{{5!}}{{3!2!}}\). D. \({5^3}\).

Phương pháp

Áp dụng công thức chỉnh hợp

Lời giải

Chọn A

Chọn 3 trong 5 màu để tô vào 3 nước khác nhau: có \(A_5^3 = \frac{{5!}}{{2!}}\) cách.

Câu 9. Khai triển của \({(x + 1)^4}\) là:

A. \({x^4} + 2{x^2} + 1\).

B. \({x^4} + 4{x^3} + 6{x^2} + 4x + 1\).

C. \({x^4} + 5{x^3} + 10{x^2} + 5x + 1\).

D. \({x^4} + 3{x^3} + 4{x^2} + 3x + 1\).

Phương pháp

Áp dụng công thức \({(a + b)^4} = {a^4} + 4{a^3}b + 6{a^2}{b^2} + 4a{b^3} + {b^4}\)

Lời giải

Chọn B

Áp dụng công thức \({(a + b)^4} = {a^4} + 4{a^3}b + 6{a^2}{b^2} + 4a{b^3} + {b^4}\)

Câu 10. Hệ số của \({x^3}\) trong khai triển của \({(2x + 1)^4}\) là:

A. 4. B. 6. C. 10. D. 32.

Phương pháp

Áp dụng công thức \({(a + b)^4} = {a^4} + 4{a^3}b + 6{a^2}{b^2} + 4a{b^3} + {b^4}\)

Lời giải

Chọn D

Số hạng chúa \({x^3}\) trong khai triển của \({(2x + 1)^4}\) là \(C_4^1{(2x)^3}.1\)

Hệ số của \({x^3}\) trong khai triển của \({(2x + 1)^4}\) là: \(C_4^1{.2^3}.1 = 32\)

Câu 11. Giả sử có khai triển \({(1 – 2x)^n} = {a_0} + {a_1}x + {a_2}{x^2} + \ldots + {a_n}{x^n}\). Tìm \({a_4}\)biết \({a_0} + {a_1} + {a_2} = 31\).

A. 80. B. \( – 80\). C. 40. D. \( – 40\).

Phương pháp

Sử dụng công thức \({(1 – 2x)^n} = {a_0} + {a_1}x + {a_2}{x^2} + \ldots + {a_n}{x^n}\)

Lời giải

Chọn A Ta có:

\({(1 – 2x)^n} = C_n^0{1^n}{( – 2x)^0} + C_n^1{n^{n – 1}}( – 2x) + C_n^2{n^{n – 2}}{( – 2x)^2} + \ldots = 1 – 2C_n^1x + 4C_n^2{x^2} + \ldots \)

Vậy \({a_0} = 1;{a_1} = – 2C_n^1;{a_2} = 4C_n^2\). Theo bài ra \({a_0} + {a_1} + {a_2} = 31\) nên ta có:

\(1 – 2C_n^1 + 4C_n^2 = 31 \Leftrightarrow 1 – 2\frac{{n!}}{{1!(n – 1)!}} + 4\frac{{n!}}{{2!(n – 2)!}} = 31 \Leftrightarrow 1 – 2n + 2n(n – 1) = 31\)

\( \Leftrightarrow 2{n^2} – 4n – 30 = 0 \Leftrightarrow {n^2} – 2n – 15 = 0 \Rightarrow n = 5\). Từ đó ta có \({a_4} = C_5^4{( – 2)^4} = 80\).

Câu 12. Hình chữ nhật có các cạnh:\(x = 2m \pm 1cm\), \(y = 5m \pm 2cm\). Diện tích hình chữ nhật và sai số tuyệt đối của giá trị đó là:

A. \(10{m^2}\) và \(900c{m^2}\).

B. \(10{m^2}\) và \(500c{m^2}\).

C. \(10{m^2}\) và \(400c{m^2}\).

D. \(10{m^2}\) và \(1404\;c{m^2}\).

Phương pháp

Nếu a là sai số gần đúng của \(\overline a \) thì \({\Delta _a} = \left| {\overline a – a} \right|\) được gọi là sai số tuyệt đối của số gần đúng a

Lời giải

Chọn D.

Ta có \(x = 2m \pm 1cm \Rightarrow 1,98m \le x \le 2,02m\) và \(y = 5m \pm 2cm \Rightarrow 4,98m \le y \le 5,02m\).

Do đó diện tích hình chữ nhật là \(S = xy\) và \(9,8604 \le S \le 10,1404 \Rightarrow S = 10 \pm 0,1404\).

Câu 13. Một hình chữ nhật có diện tích là \(S = 108,57c{m^2} \pm 0,06c{m^2}.\) Số các chữ số chắc của \(S\) là:

A. \(5.\) B. \(4.\) C. \(3.\) D. \(2.\)

Phương pháp

Nhắc lại định nghĩa số chắc:

Trong cách ghi thập phân của a, ta bảo chữ số k cuả a là chữ số đáng tin (hay chữ số chắc) nếu sai số tuyệt đối ∆_a không vượt quá một đơn vị của hàng có chữ số k.

+ Ta có sai số tuyệt đối bằng \(0,06 > 0,01 \Rightarrow \)chữ số 7 là số không chắc, \(0,06 < 0,1 \Rightarrow \)chữ số 5 là số chắc.

+ Chữ số k là số chắc thì tất cả các chữ số đứng bên trái k đều là các chữ số chắc \( \Rightarrow \) các chữ số \(1,0,8\) là các chữ số chắc. Như vậy ta có số các chữ số chắc của \(S\)là: \(1,0,8,5.\)

Lời giải

Chọn B. Số các chữ số chắc của \(S\)là: 4

A. \(1,6\% \) B. \(1,7\% \) C. \(1,662\% \) D. \(1,66\% \)

Phương pháp

Nếu a là sai số gần đúng của \(\overline a \) thì \({\Delta _a} = \left| {\overline a – a} \right|\) được gọi là sai số tuyệt đối của số gần đúng

+)Ta nói a là số gần đúng của số đúng \(\overline a \) với độ chính xác d nếu \({\Delta _a} = \left| {\overline a – a} \right| \le d\) và quy ước viết gọn là \(\overline a = a \pm d\)

+) Tỉ số \({\delta _a} = \frac{{{\Delta _a}}}{{\left| a \right|}}\) được gọi là sai số tương đối của số gần đúng a.

Lời giải

Chọn D

Giả sử\(a = 12 + {d_1},{\rm{ }}b = 10,2 + {d_2},{\rm{ }}c = 8 + {d_3}\).

Ta có \(P = a + b + c + {d_1} + {d_2} + {d_3} = 30,2 + {d_1} + {d_2} + {d_3}\).

Theo giả thiết, ta có

\( – 0,2 \le {d_1} \le 0,2\, \) ;\({\rm{ }} – 0,2 \le {d_2} \le 0,2\ \) ;\( {\rm{ }} – 0,1 \le {d_3} \le 0,1\)

Suy ra \(–0,5 \le {d_1} + {d_2} + {d_3} \le 0,5\).

Do đó \(P{\rm{ }} = 30,2{\rm{ cm}} \pm 0,5{\rm{ cm}}\).

Sai số tuyệt đối \({\Delta _P} \le 0,5\). Sai số tương đối \({\delta _P} \le \frac{d}{P} \approx 1,66\% \).

Câu 15. Số áo bán được trong một quý ở cửa hàng bán áo sơ mi nam được thống kê như sau:

Cỡ áo

Tần số

(Số áo bán được)

126

125

110

Giá trị mốt của bảng phân bố tần số trên bằng

A. \(38\). B. \(126\). C. \(42\). D. \(12\).

Phương pháp

Mốt của mẫu số liệu là giá trị có tần số lớn nhất trong bảng phân bố tần số và kí hiệu là \({M_0}\).

Lời giải

Chọn A

Vì giá trị \({x_3} = 38\) có tần số \({n_3} = 126\) lớn nhất.

A. \(6,7\) triệu đồng.

B. \(7,2\) triệu đồng.

C. \(6,8\) triệu đồng.

D. \(6,9\) triệu đồng.

Phương pháp

Sắp thứ tự mẫu số liệu gồm n số liệu thành một dãy không giảm ( hoặc không tăng).

– Nếu n là lẻ thì số liệu đứng ở vị trí thứ \(\frac{{n + 1}}{2}\) ( số đứng chính giữa) gọi là trung vị

– Nếu n là chẵn thì số trung bình cộng của hai số liệu đứng ở vị trí thứ \(\frac{n}{2}\) và \(\frac{n}{2} + 1\) gọi là trung vị

Lời giải

Chọn A

Sắp xếp thứ tự các số liệu thống kê, ta thu dược dãy tăng các số liệu sau:\(2,5\);\(3,0\);\(6,5\);\(6,7\);\(6,9\);\(7,2\); \(8,4\) (đơn vị: triệu đồng).

Số trung vị \({M_e} = 6,7\) triệu đồng.

Số các số liệu thống kê quá ít (\(n = 7 < 10\)), do đó không nên chọn số trung bình cộng làm đại diện cho các số liệu đã cho. Trong trường hợp này ta chọn số trung vị \({M_e} = 6,7\) triệu đồng làm đại diện cho tiền lương hàng tháng của \(7\) nhân viên.

Câu 17. Cho phương sai của các số liệu bằng \(4\). Tìm độ lệch chuẩn.

A. \(4\). B. \(2\). C. \(16\). D. \(8\).

Phương pháp

Độ lệch chuẩn là căn bậc hai của phương sai

Lời giải

Ta có độ lệch chuẩn là căn bậc hai của phương sai

Nên \({s_x} = \sqrt {s_x^2} = \sqrt 4 = 2\).

Câu 18. Độ lệch chuẩn là

A. Căn bậc hai của phương sai.

B. Bình phương của phương sai.

C. Một nửa của phương sai.

D. Không phải các công thức trên.

Phương pháp

Độ lệch chuẩn là căn bậc hai của phương sai

Lời giải

Chọn A.Căn bậc hai của phương sai.

Câu 19. Có 100 học sinh tham dự kì thi học sinh giỏi Toán (thang điểm 20). Kết quả cho trong bảng sau:

Khi đó độ lệch chuẩn là

A. \(1,98\). B. \(3,96\). C. \(15,23\) D. \(1,99\).

Phương pháp

Độ lệch chuẩn là căn bậc hai của phương sai

Lời giải

Chọn D

Ta có:

\(\overline x = \frac{{1.9 + 1.10 + 3.11 + 5.12 + 8.13 + 13.14 + 19.15 + 24.16 + 14.17 + 10.18 + 2.19}}{{100}} = 15,23\)

\(\overline {{x^2}} = \frac{{{{1.9}^2} + {{1.10}^2} + {{3.11}^2} + {{5.12}^2} + {{8.13}^2} + {{13.14}^2} + {{19.15}^2} + {{24.16}^2} + {{14.17}^2} + {{10.18}^2} + {{2.19}^2}}}{{100}} = 235,91\)

Phương sai của bảng số liệu là: \({s^2} = \overline {{x^2}} – {\left( {\overline x } \right)^2} = 235,91 – {15,23^2} = 3,9571\).

Độ lệch chuẩn là: \(s = \sqrt {{s^2}} = \sqrt {3,9571} \approx 1,99\).

Câu 20. Điểm thi của lớp 10C của một trường Trung học Phổ Thông được trình bày ở bảng phân bố tần số sau:

Phương sai của bảng phân bố tần số đã cho là:

A. \(0,94\) B. \(3,94.\) C. \(2,94.\) D. \(1,94.\)

Phương pháp

Cho mẫu số liêu thống kê có n giá trị \({x_1},{x_2},…,{x_n}\) và số trung bình cộng \(\overline x \).

Ta gọi số \({s^2} = \frac{{{{({x_1} – \overline x )}^2} + {{({x_2} – \overline x )}^2} + … + {{({x_n} – \overline x )}^2}}}{n}\) là phương sai của mẫu số liệu

Lời giải

Chọn D

Trong dãy số liệu về điểm thi của lớp 10C ta có:

\(\overline x = \frac{1}{n} \cdot \left( {{n_1}{x_1} + {n_2}{x_2} + … + {n_6}{x_6}} \right) = \frac{1}{{40}} \cdot \left( {7.5 + 5.6 + 10.7 + 12.8 + 4.9 + 2.10} \right) \)

\(= 7,175\)

Phương sai:

\(\begin{array}{l}{s^2} = \frac{1}{n}.\left( {{n_1}.{{\left( {{x_1} – \overline x } \right)}^2} + {n_2}.{{\left( {{x_2} – \overline x } \right)}^2} + … + {n_6}.{{\left( {{x_6} – \overline x } \right)}^2}} \right)\\\,\,\,\,\,\, = \frac{1}{{40}}.\left( {7.{{\left( {5 – 7,175} \right)}^2} + 5.{{\left( {6 – 7,175} \right)}^2} + 10.{{\left( {7 – 7,175} \right)}^2}} \right.\\\,\,\,\,\,\,\,\,\,\,\left. { + 12.{{\left( {8 – 7,175} \right)}^2} + 4.{{\left( {9 – 7,175} \right)}^2} + 2.{{\left( {10 – 7,175} \right)}^2}} \right)\\\,\,\,\,\,\, \approx 1,94.\end{array}\)

Câu 21. Điểm thi môn Toán lớp 10A₂ của một Trường trung học phổ thông được trình bày ở bảng phân bố tần số sau

Điểm thi	\(5\)	\(6\)	\(7\)	\(8\)	\(9\)	\(10\)
Tần số	\(7\)	\(5\)	\(10\)	\(12\)	\(4\)	\(2\)	\(n = 40\)

Trong các giá trị dưới đây, giá trị nào gần nhất với phương sai của bảng phân bố tần số trên?

A. \(0,94\). B. \(3,94\). C. \(2,94\). D. \(1,94\).

Phương pháp

Cho mẫu số liêu thống kê có n giá trị \({x_1},{x_2},…,{x_n}\) và số trung bình cộng \(\overline x \).

Ta gọi số \({s^2} = \frac{{{{({x_1} – \overline x )}^2} + {{({x_2} – \overline x )}^2} + … + {{({x_n} – \overline x )}^2}}}{n}\) là phương sai của mẫu số liệu

Lời giải

Trong dãy số liệu về điểm thi môn Toán lớp 10A₂ ta có

\(\overline x = \frac{1}{n}.\left( {{n_1}{x_1} + {n_2}{x_2} + … + {n_6}{x_6}} \right) = \frac{1}{{40}}.\left( {7.5 + 5.6 + 10.7 + 12.8 + 4.9 + 2.10} \right)\)

\(= 7,175\)

Phương sai là:

A. \(A \cup B = \left\{ {SSS,\,SSN,\,NSS,\,SNS,\,NNN} \right\}\).

B. \(A \cup B = \left\{ {SSS,\,NNN} \right\}\).

C. \(A \cup B = \left\{ {SSS,\,SSN,\,NSS,\,NNN} \right\}\).

D. \(A \cup B = \Omega \).

Phương pháp

Sử dụng các quy tắc đếm

Lời giải

Chọn C

\(A = \left\{ {SSS,\,SSN,\,NSS} \right\}\), \(B = \left\{ {SSS,\,NNN} \right\}\). Suy ra \(A \cup B = \left\{ {SSS,\,SSN,\,NSS,\,NNN} \right\}\).

Câu 23. Gieo ngẫu nhiên một đồng tiền cân đối và đồng chất \(5\) lần. Tính số phần tử không gian mẫu.

A. \(64\). B. \(10\). C. \(32\). D. \(16\).

Phương pháp

Sử dụng các quy tắc đếm

Lời giải

Chọn C

Mỗi lần gieo có hai khả năng nên gieo 5 lần theo quy tắc nhân ta có \({2^5} = 32\).

Số phần tử không gian mẫu là \(n\left( \Omega \right) = 32\).

Câu 24. Gieo một con súc sắc. Xác suất để mặt \(6\) chấm xuất hiện.

A. \(\frac{1}{6}\). B. \(\frac{5}{6}\). C. \(\frac{1}{2}\). D. \(\frac{1}{3}\).

Phương pháp

Sử dụng công thức tính xác suất

Lời giải

Chọn A

Gieo một con súc sắc có không gian mẫu \(\Omega = \left\{ {1;2;3;4;5;6} \right\} \Rightarrow n\left( \Omega \right) = 6\)

Xét biến cố \(A\): “mặt \(6\) chấm xuất hiện”. \(A = \left\{ 6 \right\} \Rightarrow n\left( A \right) = 1\).

Do đó \(P\left( A \right) = \frac{1}{6}\).

Câu 25. Gieo một con súc sắc cân đối và đồng chất 2 lần. Tính xác suất để tổng số chấm trong hai lần gieo nhỏ hơn 6.

A. \(\frac{2}{9}\).

B. \(\frac{{11}}{{36}}\).

C. \(\frac{1}{6}\).

D. \(\frac{5}{{18}}\).

Phương pháp

Sử dụng công thức tính xác suất

Lời giải

Chọn D

Số phần tử của không gian mẫu là: \(n\left( \Omega \right) = {6^2} = 36\).

Gọi A là biến cố “Tổng số chấm trong hai lần gieo nhỏ hơn 6”.

Tập hợp các quả của biến cố A là:

\(A = \left\{ {\left( {1;1} \right);\left( {1;2} \right);\left( {1;3} \right);\left( {1;4} \right);\left( {2;1} \right);\left( {2;2} \right);\left( {2;3} \right);\left( {3;1} \right);\left( {3;2} \right);\left( {4;1} \right)} \right\}\).

Số phần tử của biến cố A là: \(n\left( A \right) = 10\).

Xác suất của biến cố A là: \(P\left( A \right) = \frac{{10}}{{36}} = \frac{5}{{18}}\).

A. \(e = \frac{4}{5}\). B. \(e = \frac{4}{{18}}\). C. \(e = – \frac{4}{5}\). D. \(e = \frac{4}{9}\).

Phương pháp

Tâm sai \(e = \frac{c}{a}\).

Lời giải

Chọn A

Ta có \({F_1}\left( { – 4;0} \right) \Rightarrow c = 4\).

\(\begin{array}{l}{P_{\Delta M{F_1}{F_2}}} = \underbrace {M{F_1} + M{F_2}}_{2a} + {F_1}{F_2}\\ \Leftrightarrow \,\,\,18 = 2a + 2c \Leftrightarrow 18 = 2a + 8 \Leftrightarrow a = 5.\end{array}\)

Tâm sai \(e = \frac{c}{a} = \frac{4}{5}\).

Câu 27. Trong mặt phẳng toạ độ \(Oxy\), cho \(\vec a = (1;2),\vec b = (3; – 3)\). Toạ độ của vectơ \(\vec c = 3\vec a – 2\vec b\) là:

A. \(( – 3;12)\). B. \((3;12)\). C. \((9;0)\). D. \(( – 3;0)\).

Phương pháp

Trong mặt phẳng \(Oxy\), cho \(\vec a = \left( {{a_1}\,;\,{a_2}} \right)\); \(\vec b = \left( {{b_1}\,;\,{b_2}} \right)\). Tọa độ vectơ \(k\overrightarrow a + t\overrightarrow b = (k{a_1} + t{b_1};k{a_2} + t{b_2})\)

Lời giải

Chọn A.

Ta có: \(3\vec a = (3;6)\) và \( – 2\vec b = ( – 6;6)\). Suy ra \(3\vec a – 2\vec b = ( – 3;12)\).

Câu 28. Trong mặt phẳng toạ độ \(Oxy\), cho ba điểm \(A( – 1;2),B(2; – 2),C(3;1)\). Toạ độ của vectơ \(\overrightarrow {AB} + \overrightarrow {BC} \) là:

A. \(( – 4; – 1)\). B. \((4; – 1)\). C. \(( – 4;1)\). D. \((4;1)\).

Phương pháp

Với \(A({x_A};{y_A});B({x_B};{y_B})\) thì \(\overrightarrow {AB} = \left( {({x_B} – {x_A});({y_B} – {y_A})} \right)\)

Lời giải

Chọn\({\bf{B}}\).

Ta có: \(\overrightarrow {AB} + \overrightarrow {BC} = \overrightarrow {AC} = (4; – 1)\)

Câu 29. Một đường thẳng có bao nhiêu vectơ pháp tuyến?

A. 0. B. 1. C. 2. D. Vô số.

Phương pháp

Vecto pháp tuyến có giá vuông góc với đường thẳng.

Lời giải

Chọn D.

Một đường thẳng có vô số các vecto pháp tuyến.

Câu 30. Phương trình tổng quát của đường thẳng \(\Delta \) đi qua điểm \(M\left( {{x_0};{y_0}} \right)\) và có vectơ pháp tuyến \(\vec n(a;b)\) là:

A. \(\frac{{x – {x_0}}}{a} = \frac{{y – {y_0}}}{b}\).

B. \(b\left( {x – {x_0}} \right) – a\left( {y – {y_0}} \right) = 0\).

C. \(a\left( {x + {x_0}} \right) + b\left( {y + {y_0}} \right) = 0\).

D. \(a\left( {x – {x_0}} \right) + b\left( {y – {y_0}} \right) = 0\).

Phương pháp

Phương trình tổng quát của đường thẳng \(\Delta \) đi qua điểm \(M\left( {{x_0};{y_0}} \right)\) và có vectơ pháp tuyến \(\vec n(a;b)\) là: \(a\left( {x – {x_0}} \right) + b\left( {y – {y_0}} \right) = 0\)

Lời giải

Chọn D

Câu 31. Đường Hyperbol \(\frac{{{x^2}}}{{16}} – \frac{{{y^2}}}{9} = 1\) có một tiêu điểm là điểm nào dưới đây ?

A.\(\left( { – 5;0} \right)\).

B.\(\left( {0;\sqrt 7 } \right)\).

C. \(\left( {\sqrt 7 ;0} \right)\).

D. \(\left( {0;5} \right)\).

Phương pháp

Đường Hyperbol \(\frac{{{x^2}}}{{{a^2}}} – \frac{{{y^2}}}{{{b^2}}} = 1\) có tiêu điểm là \({F_1}\left( { – c;0} \right),{F_2}\left( {c;0} \right);\) với \(c = \sqrt {{a^2} + {b^2}} \)

Lời giải

Chọn A.

Ta có \(\frac{{{x^2}}}{{16}} – \frac{{{y^2}}}{9} = 1\) suy ra \(\left\{ \begin{array}{l}{a^2} = 16\\{b^2} = 9\end{array} \right. \Rightarrow {c^2} = {a^2} + {b^2} = 25 \Leftrightarrow c = 5\).

Tiêu điểm \({F_1}\left( { – 5;0} \right),{F_2}\left( {5;0} \right)\).

Câu 32. Đường elip \(\frac{{{x^2}}}{{16}} + \frac{{{y^2}}}{7} = 1\) có tiêu cự bằng

A. \(3\). B. \(9\). C. \(6\). D. \(18\).

Phương pháp

Đường elip \(\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1\) có tiêu cự \(2c\)với \(c = \sqrt {{a^2} – {b^2}} \)

Lời giải

Chọn C

Ta có: \({a^2} = 16\), \({b^2} = 7\) nên \({c^2} = {a^2} – {b^2} = 9\)\( \Rightarrow c = 3\).

Tiêu cự của elip là \(2c = 6\).

Câu 33. Trong mặt phẳng \(Oxy\), phương trình nào sau đây là phương trình của đường tròn?

A. \({x^2} + 2{y^2} – 4x – 8y + 1 = 0\).

B. \({x^2} + {y^2} – 4x + 6y – 12 = 0\).

C. \({x^2} + {y^2} – 2x – 8y + 20 = 0\).

D. \(4{x^2} + {y^2} – 10x – 6y – 2 = 0\).

Phương pháp

Phương trình đường tròn (O) có tâm I(a,b) và bán kính R là : \({(x – a)^2} + {(y – b)^2} = {R^2}\)

Lời giải

Chọn B

Để là phương trình đường tròn thì điều kiện cần là hệ số của \({x^2}\) và \({y^2}\) phải bằng nhau nên loại được đáp án A và D.

Ta có: \({x^2} + {y^2} – 2x – 8y + 20 = 0 \Leftrightarrow {\left( {x – 1} \right)^2} + {\left( {y – 4} \right)^2} + 3 = 0\) vô lý.

Ta có:\({x^2} + {y^2} – 4x + 6y – 12 = 0 \Leftrightarrow {\left( {x – 2} \right)^2} + {\left( {y + 3} \right)^2} = 25\) là phương trình đường tròn tâm \(I\left( {2; – 3} \right)\), bán kính \(R = 5\).

Câu 34. Trong mặt phẳng \(Oxy\), đường tròn \(\left( C \right):{x^2} + {y^2} + 4x + 6y – 12 = 0\) có tâm là.

A. \(I\left( { – 2; – 3} \right)\).

B. \(I\left( {2;3} \right)\).

C. \(I\left( {4;6} \right)\).

D. \(I\left( { – 4; – 6} \right)\).

Phương pháp

Phương trình đường tròn (O) có tâm I(a,b) và bán kính R là : \({(x – a)^2} + {(y – b)^2} = {R^2}\)

Lời giải

Chọn A

Ta có phương trình đường tròn là: \({\left( {x + 2} \right)^2} + {\left( {y + 3} \right)^2} = 25\).

Vậy tâm đường tròn là: \(I\left( { – 2; – 3} \right)\).

Câu 35. Đường tròn \(\left( C \right)\) đi qua hai điểm \(A\left( {1;1} \right)\), \(B\left( {5;3} \right)\) và có tâm \(I\) thuộc trục hoành có phương trình là

A. \({\left( {x + 4} \right)^2} + {y^2} = 10\).

B. \({\left( {x – 4} \right)^2} + {y^2} = 10\).

C. \({\left( {x – 4} \right)^2} + {y^2} = \sqrt {10} \).

D. \({\left( {x + 4} \right)^2} + {y^2} = \sqrt {10} \).

Phương pháp

Phương trình đường tròn có dạng \({x^2} + {y^2} – 2ax – 2by + c = 0\,\,\left( {{a^2} + {b^2} – c > 0} \right)\). và tọa độ tâm \(I(a,b)\), bán kính \(\,R = \sqrt {{a^2} + {b^2} – c} \)

Lời giải

Chọn B

Gọi \(I\left( {x;0} \right) \in Ox\); \(I{A^2} = I{B^2}\) \( \Leftrightarrow {\left( {1 – x} \right)^2} + {1^2} = {\left( {5 – x} \right)^2} + {3^2}\) \( \Leftrightarrow {x^2} – 2x + 1 + 1 = {x^2} – 10x + 25 + 9\) \( \Leftrightarrow x = 4\). Vậy tâm đường tròn là \(I\left( {4;0} \right)\) và bán kính \(R = IA = \sqrt {{{\left( {1 – 4} \right)}^2} + {1^2}} = \sqrt {10} \).

Phương trình đường tròn \(\left( C \right)\) có dạng \({\left( {x – 4} \right)^2} + {y^2} = 10\).

Tự luận ( 3 điểm)

a) Số học sinh mỗi khối là bằng nhau?

b) Có ít nhất 5 học sinh khối \(A\) và có đúng 2 học sinh khối \(C\)?

Phương pháp

Sử dụng các quy tắc đếm

Lời giải:

a) Số cách chọn 5 học sinh mỗi khối \((A,B,C)\) lần lượt là: \(C_{15}^5,C_{10}^5,C_5^5\).

Vậy số cách chọn thỏa mãn là \(C_{15}^5 \times C_{10}^5 \times C_5^5 = 756756\) (cách).

b) Ta sử dụng quy tắc loại trừ như Lời giải sau:

Xét bài toán 1: Chọn 2 học sinh khối \(C,13\) học sinh khối \(B\) hoặc khối \(A\): có \(C_5^2C_{25}^{13}\) cách.

Xét bài toán 2: Chọn 2 học sinh khối \(C,13\) học sinh khối \(B\) và khối \(A\) nhưng không thỏa mãn yêu cầu đề bài.

– Trường hợp 1: Chọn 2 học sinh khối \(C,10\) học sinh khối \(B\) và 3 học sinh khối A có \(C_5^2C_{10}^{10}C_{15}^3\) cách.

– Trường hợp 2: Chọn 2 học sinh khối \(C,9\) học sinh khối \(B\) và 4 học sinh khối A có \(C_5^2C_{10}^9C_{15}^4\) cách.

Vậy số cách chọn thỏa mãn là \(C_5^2C_{25}^{13} – C_5^2C_{10}^{10}C_{15}^3 – C_5^2C_{10}^9C_{15}^4 = 51861950\) (cách).

Câu 2. Cho biểu thức \(Q = {(xy – 1)^5}\).

a) Viết khai triển biểu thức \(Q\) bằng nhị thức Newton.

b) Tìm số hạng có chứa \({x^2}{y^2}\) trong khai triển trên.

Phương pháp

Sử dụng công thức khai triển nhị thức Newton

Lời giải

a) Ta có: \(Q = {(xy – 1)^5} = C_5^0{(xy)^5} + C_5^1{(xy)^4}( – 1) + C_5^2{(xy)^3}{( – 1)^2}\)

\(\begin{array}{l} + C_5^3{(xy)^2}{( – 1)^3} + C_5^4(xy){( – 1)^4} + C_5^5{( – 1)^5}\\ = {x^5}{y^5} – 5{x^4}{y^4} + 10{x^3}{y^3} – 10{x^2}{y^2} + 5xy – 1.\end{array}\)

b) Số hạng có chứa \({x^2}{y^2}\) trong khai triển là \( – 10{x^2}{y^2}\).

80 65 51 48 45 61 30 35 84 83 60 58 75

72 68 39 41 54 61 72 75 72 61 58 65

a) Tìm phương sai và độ lệch chuẩn. Nhận xét gì về các kết quả nhận được.

b) Tìm khoảng biến thiên, khoảng tứ phân vị

c) Tìm giá trị bất thường

Phương pháp

a) – Cho mẫu số liêu thống kê có n giá trị \({x_1},{x_2},…,{x_n}\) và số trung bình cộng \(\overline x \).

Ta gọi số \({s^2} = \frac{{{{({x_1} – \overline x )}^2} + {{({x_2} – \overline x )}^2} + … + {{({x_n} – \overline x )}^2}}}{n}\) là phương sai của mẫu số liệu

– Căn bậc hai của phương sai gọi là Độ lệch chuẩn của mẫu số liệu thống kê

b) – Ta có thể tính khoảng bến thiên R của mẫu số liệu theo công thức \(R = {x_{\max }} – {x_{\min }}\), trong đó \({x_{\max }}\) là giá trị lớn nhất, \({x_{\min }}\)là giá trị nhỏ nhất của mẫu số liệu đó.

– Giả sử \({Q_1},{Q_2},{Q_3}\) là tứ phân vị của mẫu số liệu. Ta gọi hiệu \({\Delta _Q} = {Q_3} – {Q_1}\) là khoảng tứ phân vị của mẫu số liệu đó.

Lời giải

a) Tìm phương sai và độ lệch chuẩn. Nhận xét gì về các kết quả nhận được.

Ta lập bảng phân bố tần số như sau:

Điểm	30 35 39 41 45 48 50 51 54 58 60 61 65 68 72 75 80 83 84
Tần số	1 1 1 1 1 1 1 1 1 1 1 3 2 1 3 2 1 1 1

Ta có:

\( x = \frac{1}{n}\left( {{n_1}{x_1} + {n_2}{x_2} + … + {n_k}{x_k}} \right)\\ \)

\(= \frac{1}{{25}}\left( {1.30 + 1.35 + 1.39 + 1.41 + 1.45 + 1.48 + …. + 1.60+ 3.61 + 2.65 + 1.68 + 3.72 + 2.75 + 1.80 + 1.83 + 1.84} \right)\\ = 60,\)

Phương sai:

\(s_x^2 = \frac{1}{n}\left[ {{n_1}{{({x_1} – \overline x )}^2} + {n_2}{{({x_2} – \overline x )}^2} + … + {n_k}{{({x_k} – \overline x )}^2}} \right] = 216,8\)

Độ lệch chuẩn \({s_x} = \sqrt {s_x^2} = \sqrt {216,8} \approx 14,724\)

Nhận xét: mức độ chênh lệch điểm giữa các giá trị là khá lớn

b) Tìm khoảng biến thiên, khoảng tứ phân vị

Khoảng biến thiên \(84 – 30 = 54\)

Nửa số liệu bên trái là gồm 12 giá trị, hai phần tử chính giữa là 48,50 .

Do đó, \({Q_1} = (48 + 50):2 = 49\).

Nửa số liệu bên phải là gồm 12 giá tri, hai phần tử chính giữa là 72,72.

Do đó, \({Q_3} = (72 + 72):2 = 72\).

Vậy khoảng tứ phân vị cho mẫu số liệu là \({\Delta _Q} = 72 – 49 = 23\).

c) Tìm giá trị bất thường

Không có giá trị bất thường

Câu 4. Cho tam giác \(ABC\) với \(A( – 1; – 2)\) và phương trình đường thẳng chứa cạnh \(BC\) là \(x – y + 4 = 0\).

a) Viết phương trình đường cao \(AH\) của tam giác.

b) Viết phương trình đường trung bình ứng với cạnh đáy \(BC\) của tam giác.

Phương pháp

Lời giải

a) Đường cao \(AH\) vuông góc với \(BC\) nên nhận \(\vec u = (1; – 1)\) làm vectơ chỉ phương, suy ra \(AH\) có một vectơ pháp tuyến là \(\vec n = (1;1)\).

Phương trình tổng quát \(AH:1(x + 1) + 1(y + 2) = 0\) hay \(x + y + 3 = 0\).

b) Chọn điểm \(K(0;4)\) thuộc \(BC\), gọi \(E\) là trung điểm đoạn \(AK\) nên \(E\left( { – \frac{1}{2};1} \right)\). Gọi \(d\) là đường trung bình ứng với cạnh đáy \(BC\) của tam giác \(ABC\), suy ra \(d\) qua \(E\) và có một vectơ pháp tuyến .

Phương trình tổng quát \(d:1\left( {x + \frac{1}{2}} \right) – 1(y – 1) = 0\) hay \(2x – 2y + 3 = 0\).