Lời giải Đề bài Đề thi học kì 1 Toán 10 – Đề số 4 – Đề thi đề kiểm tra Toán lớp 10 Cánh diều.
Câu hỏi/Đề bài:
I. Phần trắc nghiệm (5 điểm – 25 câu)
Câu 1: Cho mệnh đề chứa biến với\(x\) là số thực. Mệnh đề nào sau đây là đúng:
A. \(P\left( 3 \right)\). B. \(P\left( 4 \right)\). C. \(P\left( 1 \right)\). D. \(P\left( 5 \right)\).
Câu 2: Cho mệnh đề “\(\forall x \in R,{x^2} – x + 7 < 0\)”. Hỏi mệnh đề nào là mệnh đề phủ định của mệnh đề trên?
A. \(\exists x \in R,{x^2} – x + 7 \ge 0\). B. \(\forall x \in R,{x^2} – x + 7 > 0\).
C. \(\forall x \in R,{x^2} – x + 7 < 0\) . D. \(\cancel{\exists }x \in R,{x^2} – x + 7 < 0\).
Câu 3: Cho hai tập hợp \(A = \left\{ {1;2;3} \right\}\) và \(B = \left\{ {1;2;3;4;5} \right\}.\) Có tất cả bao nhiêu tập \(X\) thỏa \(A \subset X \subset B?\)
A. \(4.\) B. \(5.\) C. \(6.\) D. \(8.\)
Câu 4: Hãy liệt kê các phần tử của tập \(X = \left\{ {x \in \mathbb{Q}\left| {\left( {{x^2} – x – 6} \right)\left( {{x^2} – 5} \right) = 0} \right.} \right\}.\)
A. \(X = \left\{ {\sqrt 5 ;3} \right\}.\) B. \(X = \left\{ { – \sqrt 5 ; – 2;\sqrt 5 ;3} \right\}.\)
C. \(X = \left\{ { – 2;3} \right\}.\) D. \(X = \left\{ { – \sqrt 5 ;\sqrt 5 } \right\}.\)
Câu 5: Cho hai tập hợp \(A = \left\{ {0;1;2;3;4} \right\},\;B = \left\{ {2;3;4;5;6} \right\}\). Tìm \(X = \left( {A\backslash B} \right) \cap \left( {B\backslash A} \right).\)
A. \(X = \left\{ {0;1;5;6} \right\}.\) B. \(X = \left\{ {1;2} \right\}.\) C. \(X = \left\{ 5 \right\}.\) D. \(X = \emptyset .\)
Câu 6: Biểu diễn trên trục số các tập hợp \(\left[ { – 7,3} \right]\backslash \left[ { – 4,0} \right]\) là hình nào dưới đây.
A. 
B. 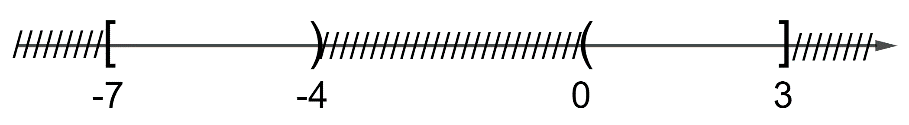
C. 
D. 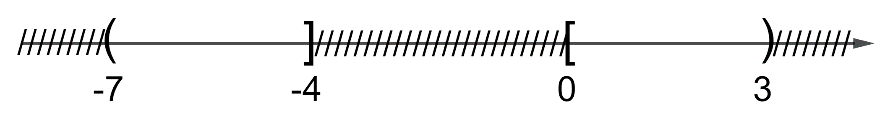
Câu 7: Miền nghiệm của bất phương trình: \(3x + 2\left( {y + 3} \right) > 4\left( {x + 1} \right) – y + 3\) là nửa mặt phẳng chứa điểm:
A. \(\left( {3;0} \right).\) B. \(\left( {3;1} \right).\) C. \(\left( {2;1} \right).\) D. \(\left( {0;0} \right).\)
Câu 8: Cho hệ bất phương trình \(\left\{ \begin{array}{l}x + 3y – 2 \ge 0\\2x + y + 1 \le 0\end{array} \right.\). Trong các điểm sau, điểm nào thuộc miền nghiệm của hệ bất phương trình?
A. \(M\left( {0;1} \right).\) B. \(N\left( {-1;1} \right).\) C. \(P\left( {1;3} \right).\) D. \(Q\left( {-1;0} \right).\)
Câu 9: Tìm tập xác định \({\rm{D}}\) của hàm số \(y = \frac{{{x^2} + 1}}{{{x^2} + 3x – 4}}.\)
A. \({\rm{D}} = \left\{ {1; – 4} \right\}.\) B. \({\rm{D}} = \mathbb{R}\backslash \left\{ {1; – 4} \right\}.\) C. \({\rm{D}} = \mathbb{R}\backslash \left\{ {1;4} \right\}.\) D. \({\rm{D}} = \mathbb{R}.\)
Câu 10: Tìm tập xác định \({\rm{D}}\) của hàm số \(y = \frac{{\sqrt {6 – 3x} + \sqrt {x + 2} }}{{5x}}.\)
A. \({\rm{D}} = \left[ { – 2;2} \right].\) B. \({\rm{D}} = \left( { – 2;2} \right)\backslash \left\{ 0 \right\}.\) C. \({\rm{D}} = \left[ { – 2;2} \right]\backslash \left\{ 0 \right\}.\) D. \({\rm{D}} = \mathbb{R}.\)
Câu 11: Cho hàm số \(f\left( x \right) = 4 – 3x\). Khẳng định nào sau đây đúng?
A. Hàm số đồng biến trên \(\left( { – \infty ;\frac{4}{3}} \right)\). B. Hàm số nghịch biến trên \(\left( {\frac{4}{3}; + \infty } \right)\).
C. Hàm số đồng biến trên \(\mathbb{R}\). D. Hàm số đồng biến trên \(\left( {\frac{3}{4}; + \infty } \right)\).
Câu 12: Cho hàm số \(y = \frac{{\sqrt {x – 2} – 2}}{{x – 6}}\). Điểm nào sau đây thuộc đồ thị hàm số:
A. \((6;0)\). B. \((2; – 0,5)\). C. \((2;0,5)\). D. \((0;6)\).
Câu 13: Giá trị nhỏ nhất của hàm số \(y = x – 2\sqrt {x – 3} \) là:
A. – 2 B. – 1 C. 0 D. 2
Câu 14: Tọa độ đỉnh của parabol \(y = – 2{x^2} – 4x + 6\) là
A. \(I\left( { – 1;8} \right)\). B. \(I\left( {1;0} \right)\). C. \(I\left( {2; – 10} \right)\). D. \(I\left( { – 1;6} \right)\).
Câu 15: Tính giá trị biểu thức \(P = \sin {30^ \circ }\cos {60^ \circ } + \sin {60^ \circ }\cos {30^ \circ }.\)
A. \(P = 1.\) B. \(P = 0.\) C. \(P = \sqrt 3 .\) D. \(P = – \sqrt 3 .\)
Câu 16: Tam giác \(ABC\) có \(\widehat B = 60^\circ ,\;\widehat C = 45^\circ \) và \(AB = 5\). Tính độ dài cạnh \(AC\).
A. \(AC = \frac{{5\sqrt 6 }}{2}.\) B. \(AC = 5\sqrt 3 .\) C. \(AC = 5\sqrt 2 .\) D. \(AC = 10.\)
Câu 17: Tam giác \(ABC\) có \(AB = 4,\;BC = 6,\;AC = 2\sqrt 7 \). Điểm \(M\) thuộc đoạn \(BC\) sao cho \(MC = 2MB\). Tính độ dài cạnh \(AM\).
A. \(AM = 4\sqrt 2 .\) B. \(AM = 3.\) C. \(AM = 2\sqrt 3 .\) D. \(AM = 3\sqrt 2 .\)
Câu 18: Tam giác ABC có \(\angle A = {45^0},{\mkern 1mu} {\mkern 1mu} c = 6,{\mkern 1mu} {\mkern 1mu} \angle B = {75^0}\). Độ dài bán kính đường tròn ngoại tiếp tam giác bằng:
A. \(8\sqrt 3 \) B. \(2\sqrt 3 \) C. \(6\sqrt 3 \) D. \(4\sqrt 3 \)
Câu 19: Cho tam giác ABC có trung tuyến BM và trọng tâm \(G\). Đặt \(\overrightarrow {BC} {\rm{\;}} = \vec a,{\mkern 1mu} {\mkern 1mu} \overrightarrow {BA} {\rm{\;}} = b\). Hãy phân tích vectơ \(\overrightarrow {BG} \) theo \(\vec a\) và \(\vec b\).
A. \(\overrightarrow {BG} {\rm{\;}} = \frac{1}{3}\vec a + \frac{1}{3}\vec b\) B. \(\overrightarrow {BG} {\rm{\;}} = \frac{2}{3}\vec a + \frac{2}{3}\vec b\) C. \(\overrightarrow {BG} {\rm{\;}} = \frac{1}{3}\vec a + \frac{2}{3}\vec b\) D. \(\overrightarrow {BG} {\rm{\;}} = \frac{2}{3}\vec a + \frac{1}{3}\vec b\)
Câu 20: Cho tam giác \(ABC\) với \(M,\;N,\;P\) lần lượt là trung điểm của \(BC,\;CA,\;AB\). Khẳng định nào sau đây sai?
A. \(\overrightarrow {AB} + \overrightarrow {BC} + \overrightarrow {CA} = \overrightarrow 0 .\) B. \(\overrightarrow {AP} + \overrightarrow {BM} + \overrightarrow {CN} = \overrightarrow 0 .\)
C. \(\overrightarrow {MN} + \overrightarrow {NP} + \overrightarrow {PM} = \overrightarrow 0 .\) D. \(\overrightarrow {PB} + \overrightarrow {MC} = \overrightarrow {MP} .\)
Câu 21: Gọi \(O\) là tâm hình vuông \(ABCD\). Tính \(\overrightarrow {OB} – \overrightarrow {OC} \).
A. \(\overrightarrow {OB} – \overrightarrow {OC} = \overrightarrow {BC} .\) B. \(\overrightarrow {OB} – \overrightarrow {OC} = \overrightarrow {DA} .\)
C. \(\overrightarrow {OB} – \overrightarrow {OC} = \overrightarrow {OD} – \overrightarrow {OA} .\) D. \(\overrightarrow {OB} – \overrightarrow {OC} = \overrightarrow {AB} .\)
Câu 22: Tam giác \(ABC\) có \(AB = AC = a\) và \(\widehat {BAC} = 120^\circ \). Tính \(\left| {\overrightarrow {AB} + \overrightarrow {AC} } \right|.\)
A. \(\left| {\overrightarrow {AB} + \overrightarrow {AC} } \right| = a\sqrt 3 .\) B. \(\left| {\overrightarrow {AB} + \overrightarrow {AC} } \right| = a.\)
C. \(\left| {\overrightarrow {AB} + \overrightarrow {AC} } \right| = \frac{a}{2}.\) D. \(\left| {\overrightarrow {AB} + \overrightarrow {AC} } \right| = 2a.\)
Câu 23: Cho hình vuông \(ABCD\) cạnh \(a.\) Tính \(\overrightarrow {AB} .\overrightarrow {AC} .\)
A. \(\overrightarrow {AB} .\overrightarrow {AC} = {a^2}.\) B. \(\overrightarrow {AB} .\overrightarrow {AC} = {a^2}\sqrt 2 .\) C. \(\overrightarrow {AB} .\overrightarrow {AC} = \frac{{\sqrt 2 }}{2}{a^2}.\) D. \(\overrightarrow {AB} .\overrightarrow {AC} = \frac{1}{2}{a^2}.\)
Câu 24: Cho hình vuông \(ABCD\) cạnh \(a.\) Tính \(\left| {\overrightarrow {AB} – \overrightarrow {DA} } \right|.\)
A. \(\left| {\overrightarrow {AB} – \overrightarrow {DA} } \right| = 0.\) B. \(\left| {\overrightarrow {AB} – \overrightarrow {DA} } \right| = a.\) C. \(\left| {\overrightarrow {AB} – \overrightarrow {DA} } \right| = a\sqrt 2 .\) D. \(\left| {\overrightarrow {AB} – \overrightarrow {DA} } \right| = 2a.\)
II. Tự luận (4 điểm)
Câu 1: Trong lớp 10C có 40 học sinh trong đó có 20 em thích môn Toán, 18 em thích môn Anh và 12 em không thích môn nào. Tính số học sinh thích cả hai môn Toán và Anh.
Câu 2:
a. Xác định parabol \(\left( P \right):y = 2{x^2} + bx + c,\) biết rằng \(\left( P \right)\) đi qua điểm \(M\left( {0;4} \right)\) và có trục đối xứng \(x = 1.\)
b. Xét sự biến thiên và vẽ đồ thị hàm số trên.
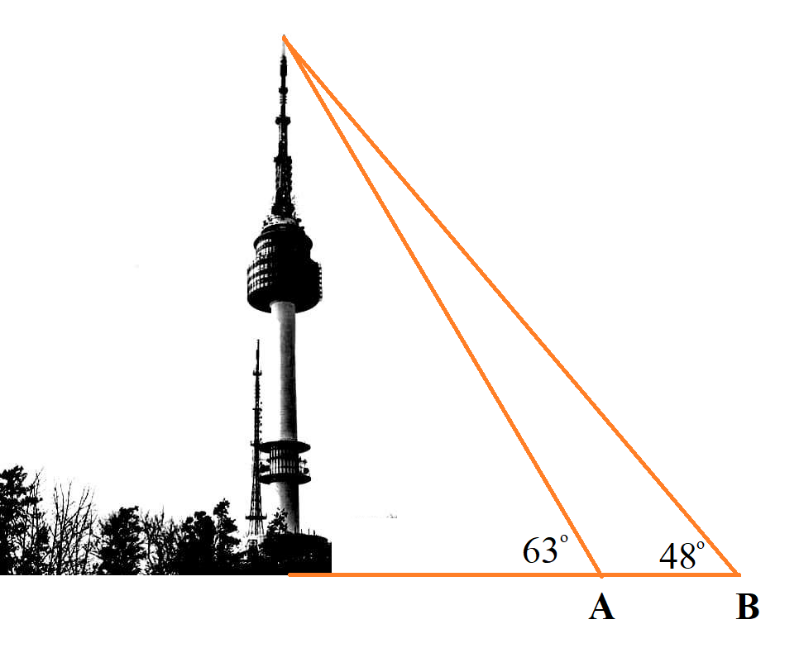
Câu 3: Để đo chiều cao ngọn tháp, người ta đánh dấu hai điểm A, B trên mặt đất sao cho ba điểm A, B và chân tháp thẳng hàng; AB = 100 m. Tại A và B người ta xác định được góc nhìn tháp (như hình vẽ) lần lượt là \({63^ \circ }\) và \({48^ \circ }\). Tính chiều cao của tháp.
Câu 4. Cho tam giác ABC. Gọi M là trung điểm của AB và N là điểm trên cạnh AC sao cho NC=2NA. Gọi K là trung điểm của MN.
a) Chứng minh rằng: \(\overrightarrow {AK} = \frac{1}{4}\overrightarrow {AB} + \frac{1}{6}\overrightarrow {AC} \)
b) Gọi D là trung điểm của BC. Chứng minh rằng: \(\overrightarrow {KD} = \frac{1}{4}\overrightarrow {AB} + \frac{1}{3}\overrightarrow {AC} \).
—– HẾT —–