Giải Đề bài Đề thi học kì 1 Toán 10 – Đề số 3 – Đề thi đề kiểm tra Toán lớp 10 Cánh diều.
Câu hỏi/Đề bài:
Phần I: Trắc nghiệm (6 điểm).
Câu 1: Cho đồ thị hàm số \(y = {x^3}\) như hình bên:
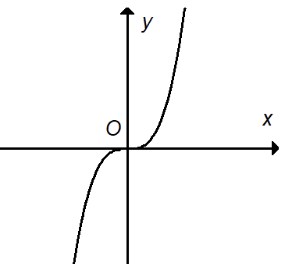
Khẳng định nào sau đây sai?
A. Hàm số đồng biến trên khoảng \(\left( { – \infty ;0} \right)\). B. Hàm số đồng biến trên khoảng \(\left( {0; + \infty } \right)\). C. Hàm số đồng biến trên khoảng \(\left( { – \infty ; + \infty } \right)\). D. Hàm số đồng biến tại gốc tọa độ O.
Câu 2: Hàm số \(y = \frac{{9x – 1}}{{x + 6}}\) xác định khi nào?
A. \(9x – 1 \ge 0\). B. \(x + 6 \ge 0\). C. \(9x – 1 \ne 0\). D. \(x + 6 \ne 0\).
Câu 3: Đồ thị hàm số \(y = 3{x^2} + 4x – 1\) nhận đường thẳng nào dưới đây làm trục đối xứng?
A. \(x = \frac{4}{3}\) B. \(y = \frac{2}{3}\) C. \(x = {\rm{ \;}} – \frac{2}{3}\) D. \(x = {\rm{ \;}} – \frac{1}{3}\)
Câu 4: Hàm số \(y = 2{x^2} + 16x – 25\) đồng biến trên khoảng:
A. \(\left( { – \infty ; – 4} \right).\) B. \(\left( { – \infty ;8} \right).\) C. \(\left( { – 6; + \infty } \right).\) D. \(\left( { – 4; + \infty } \right).\)
Câu 5: Cho \(\overrightarrow {AB} {\rm{ \;}} \ne \vec 0\) và một điểm \(C\), có bao nhiêu điểm \(D\) thỏa mãn \(\overrightarrow {AB} {\rm{ \;}} = \overrightarrow {CD} .\)
A. \(1\) B. \(2\) C. \(0\) D. Vô số.
Câu 6: Cho lục giác đều ABCDEF tâm \(O\). Số các vectơ khác vectơ không, cùng phương với \(\overrightarrow {OC} \) có điểm đầu và điểm cuối là các đỉnh của lục giác là:
A. \(4\) B. \(6\) C. \(7\) D. \(9\).
Câu 7: Cho ba điểm \(M,{\mkern 1mu} {\mkern 1mu} N,{\mkern 1mu} {\mkern 1mu} P\) phân biệt. Đẳng thức nào sau đây sai?
A. \(\overrightarrow {PM} {\rm{\;}} + \overrightarrow {MN} {\rm{\;}} = \overrightarrow {PN} .\) B. \(\overrightarrow {MP} {\rm{\;}} – \overrightarrow {MN} {\rm{\;}} = \overrightarrow {NP} .\) C. \(\overrightarrow {NM} {\rm{\;}} – \overrightarrow {NP} {\rm{\;}} = \overrightarrow {PM} .\) D. \(\overrightarrow {NM} {\rm{\;}} + \overrightarrow {PM} {\rm{\;}} = \overrightarrow {NP} .\)
Câu 8: Cho đoạn thẳng MN lấy điểm \(P\) sao cho \(\overrightarrow {MN} {\rm{\;}} = {\rm{\;}} – 3\overrightarrow {MP} \). Điểm \(P\) được xác định bởi hình vẽ nào sau đây?
A.  B.
B.  C.
C.  D.
D. 
Câu 9: Cho hai vector \(\vec a,\vec b\) thỏa \(\left| {\vec a} \right| = 2,\left| {\vec b} \right| = 3,\left( {\vec a;\vec b} \right) = {120^0}\). Tính tích vô hướng \(\vec a.\vec b\).
A. \( – 3\). B. \(3\). C. \( – 3\sqrt 3 \). D. \(3\sqrt 3 \).
Câu 10: Cho hàm số \(f\left( x \right) = \left\{ {\begin{array}{*{20}{l}}{\frac{{2\sqrt {x + 2} {\rm{ \;}} – 3}}{{x – 1}}{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} x \ge 2}\\{{x^2} + 1{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} x < 2}\end{array}} \right.\). Tính \(P = f\left( 2 \right) + f\left( { – 2} \right)\).
A. \(P = \frac{8}{3}\) B. \(P = 4\) C. \(P = 6\) D. \(P = \frac{5}{3}\)
Câu 11: Bảng biến thiên sau là của hàm số nào?
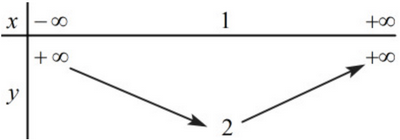
A. \(y = {x^2} + 2x – 1\) B. \(y = {x^2} – 2x + 2\) C. \(y = 2{x^2} – 4x + 4\) D. \(y = {\rm{ \;}} – 3{x^2} + 6x – 1\)
Câu 12: Đường thẳng \(d:y = x + 3\) cắt parabol \(\left( P \right):y = 3{x^2} + 10x + 3\) tại hai điểm có hoành độ lần lượt là
A. \(x = {\rm{\;}} – \frac{1}{3},{\mkern 1mu} x = 3\). B. \(x = {\rm{\;}} – \frac{1}{3},{\mkern 1mu} x = {\rm{\;}} – 3\). C. \(x = {\rm{\;}} – 3,{\mkern 1mu} x = 3\). D. \(x = {\rm{\;}} – 3,{\mkern 1mu} x = 0\).
Câu 13: Một vật được ném lên trên cao và độ cao của nó so với mặt đất được cho bởi công thức \(h\left( t \right) = 3 + 10t – 2{t^2}\left( m \right)\), với \(t\) là thời gian tính bằng giây \(\left( s \right)\) kể từ lúc bắt đầu ném. Độ cao cực đại mà vật đó có thể đạt được so với mặt đất bằng bao nhiêu mét?
A. \(\frac{{31}}{2}\) B. \(\frac{{33}}{2}\) C. 15 D. 16
Câu 14: Cho \(f\left( x \right) = m{x^2} – 2x – 1\). Xác định \(m\) để \(f\left( x \right) < 0\) với mọi \(x \in \mathbb{R}\).
A. \(m < {\rm{ \;}} – 1\) B. \(m < 0\) C. \( – 1 < m < 0\) D. \(m < 1\) và \(m \ne 0\).
Câu 15: Trong các tập hợp sau đây, tập nào có chứa phần tử không phải là nghiệm của bất phương trình \({x^2} – 8x + 7 \ge 0\)?
A. \(\left( { – \infty ;{\mkern 1mu} {\mkern 1mu} 0} \right]\) B. \(\left[ {8;{\mkern 1mu} {\mkern 1mu} + \infty } \right)\) C. \(\left( { – \infty ;{\mkern 1mu} {\mkern 1mu} 1} \right]\) D. \(\left[ {6;{\mkern 1mu} {\mkern 1mu} + \infty } \right)\)
Câu 16: Giải phương trình sau \(\sqrt {x + 7} {\rm{\;}} = x + 1\)
A. \(x = 1.\) B. \(x = 2.\) C. \(x = – 3.\) D. \(x = 3.\)
Câu 17: Cho hình thoi ABCD tâm \(O\), cạnh bằng \(a\), và góc \(A\) bằng \({60^0}\). Kết luận nào đúng?
A. \(\left| {\overrightarrow {OA} } \right| = a\) B. \(\left| {\overrightarrow {OA} } \right| = \frac{{a\sqrt 3 }}{2}\) C. \(\left| {\overrightarrow {OA} } \right| = \frac{{a\sqrt 2 }}{2}\) D. \(\left| {\overrightarrow {OA} } \right| = \left| {\overrightarrow {OB} } \right|\)
Câu 18: Cho tam giác ABC.Tập hợp các điểm \(M\)thỏa mãn\(\left| {\overrightarrow {MB} {\rm{ \;}} – \overrightarrow {MC} } \right| = \left| {\overrightarrow {BM} {\rm{ \;}} – \overrightarrow {BA} } \right|\)là?
A. đường thẳng AB.
B. trung trực đoạn BC.
C. đường tròn tâm A, bán kính BC.
D. đường thẳng qua \(A\) và song song vơi BC.
Câu 19: Cho tam giác ABC có AM là đường trung tuyến. Gọi I là trung điểm của AM. Trong các mệnh đề sau, mệnh đề nào đúng?
A. \(\overrightarrow {IA} + \overrightarrow {IB} + \overrightarrow {IC} = \overrightarrow 0 \) B. \(\overrightarrow {IA} {\rm{\;}} + 2\overrightarrow {IB} {\rm{\;}} + 2\overrightarrow {IC} {\rm{\;}} = \vec 0\)
C. \(2\overrightarrow {IA} {\rm{\;}} + \overrightarrow {IB} {\rm{\;}} + \overrightarrow {IC} {\rm{\;}} = \vec 0\) D. \(2\overrightarrow {IA} {\rm{\;}} – \overrightarrow {IB} {\rm{\;}} – \overrightarrow {IC} {\rm{\;}} = \vec 0\)
Câu 20: Cho đoạn thẳng AB và \(M\) là một điểm nằm trên đoạn AB sao cho \(AM = \frac{1}{5}AB\). Giá trị của \(k\) để có đẳng thức \(\overrightarrow {AM} {\rm{\;}} = k.\overrightarrow {AB} \) là:
A. \(k = {\rm{\;}} – \frac{1}{5}\) B. \(k = \frac{1}{5}\) C. \(k = 5\) D. \(k = {\rm{\;}} – 5\)
Câu 21: Cho hai vectơ \(\vec a\) và \(\vec b\) khác \(\vec 0\). Xác định góc \(\alpha \) giữa hai vectơ \(\vec a\) và \(\vec b\) biết \(\vec a.\vec b{\rm{\;}} = {\rm{\;}} – \left| {\vec a} \right|.\left| {\vec b} \right|\).
A. \(\alpha {\rm{\;}} = {0^0}\). B. \(\alpha {\rm{\;}} = {45^0}\). C. \(\alpha {\rm{\;}} = {90^0}\). D. \(\alpha {\rm{\;}} = {180^0}\).
Câu 22: Tìm tất cả các giá trị thực của tham số \(m\) để hàm số \(y = \frac{{2x + 1}}{{{x^2} – 2x + m – 2}}\) xác định trên \(\mathbb{R}\).
A. \(m > 3\) B. \(m \ge 3\) C. \(m < 3\) D. \(m \le 3\)
Câu 23: Parabol \(y = a{x^2} + bx + c\) đi qua A(0;-1), B(1;-1), C(-1;1) có phương trình là:
A. \(y = {x^2} – x + 1\) B. \(y = {x^2} – x – 1\) C. \(y = {x^2} + x – 1\) D. \(y = {x^2} + x + 1\)
Câu 24: Giá trị dương lớn nhất để hàm số \(y = \sqrt {5 – 4x – {x^2}} \) xác định là
A. \(1\) B. \(2\) C. \(3\) D. \(4\)
Câu 25: Cho tam giác ABC nhọn, có H là trực tâm. \(\Delta BHC\) nội tiếp \(\left( {I,R} \right)\). Gọi M là trung điểm BC. Khẳng định nào sau đây là đúng
A. \(\overrightarrow {MB} ,\overrightarrow {MC} \)cùng hướng. B. \(\overrightarrow {HA} ,\overrightarrow {IM} \)cùng hướng. C. \(\overrightarrow {MB} ,\overrightarrow {BC} \)cùng hướng. D. Cả A, B, C đều sai.
Câu 26: Cho hình bình hành ABCD, \(\vec u{\rm{ \;}} = \overrightarrow {AC} {\rm{ \;}} + \overrightarrow {BD} \). Khẳng định nào sau đây đúng?
A. \(\vec u\) cùng hướng với \(\overrightarrow {AB} \) B. \(\vec u\) cùng hướng với \(\overrightarrow {AD} \)
C. \(\vec u\) ngược hướng với \(\overrightarrow {AB} \) D. \(\vec u\) ngược hướng với \(\overrightarrow {AD} \)
Câu 27: Cho tam giác ABC, có \(M \in BC\) sao cho \(\overrightarrow {MB} {\rm{\;}} = 3\overrightarrow {MC} \). Hãy phân tích \(\overrightarrow {AM} \) theo hai vectơ \(\vec u = \overrightarrow {AB} ,{\mkern 1mu} {\mkern 1mu} \vec v = \overrightarrow {AC} \).
A. \(\overrightarrow {AM} {\rm{\;}} = \frac{1}{2}\vec u + \frac{3}{2}\vec v\) B. \(\overrightarrow {AM} {\rm{\;}} = \frac{{ – 1}}{2}\vec u + \frac{3}{2}\vec v\)
C. \(\overrightarrow {AM} {\rm{\;}} = \frac{{ – 1}}{2}\vec u – \frac{3}{2}\vec v\) D. \(\overrightarrow {AM} {\rm{\;}} = \frac{1}{2}\vec u – \frac{3}{2}\vec v\)
Câu 28: Cho hình bình hành ABCD có \(AB = 8cm\), \(AD = 12cm\) , góc \(\angle ABC\) nhọn và diện tích tam giác ABC bằng \(27{\mkern 1mu} c{m^2}\) Khi đó \(\cos \left( {\overrightarrow {AB} ,\overrightarrow {BC} } \right)\) bằng
A. \(\cos \left( {\overrightarrow {AB} ,\overrightarrow {BC} } \right) = {\rm{\;}} – \frac{{5\sqrt 7 }}{{16}}\) B. \(\cos \left( {\overrightarrow {AB} ,\overrightarrow {BC} } \right) = \frac{{5\sqrt 7 }}{{16}}\)
C. \(\cos \left( {\overrightarrow {AB} ,\overrightarrow {BC} } \right) = \frac{{2\sqrt 7 }}{{16}}\) D. \(\cos \left( {\overrightarrow {AB} ,\overrightarrow {BC} } \right) = {\rm{\;}} – \frac{{2\sqrt 7 }}{{16}}\)
Câu 29: Cho tam giác ABC đều, cạnh bằng \(a\), điểm \(M\) thuộc đường tròn ngoại tiếp tam giác ABC và thỏa mãn \(\overrightarrow {MA} .\overrightarrow {MB} {\rm{\;}} + \overrightarrow {MB} .\overrightarrow {MC} {\rm{\;}} + \overrightarrow {MC} .\overrightarrow {MA} {\rm{\;}} = \frac{{{a^2}}}{4}\). Bán kính đường tròn đó là
A. \(R = a\) B. \(R = \frac{a}{4}\) C. \(R = \frac{a}{2}\) D. \(R = \frac{{3a}}{2}\)
Câu 30: Cho hàm số \(y = a{x^2} + bx + c,{\mkern 1mu} {\mkern 1mu} a \ne 0,\) biết hàm số đạt giá trị lớn nhất trên \(\mathbb{R}\) bằng 4 khi \(x = {\rm{\;}} – 1\) và tổng bình phương các nghiệm của phương trình \(y = 0\) bằng 10. Hàm số đã cho là hàm số nào sau đây?
A. \(y = {x^2} + 2x – 3\). B. \(y = {\rm{\;}} – 2{x^2} – 4x + 2\). C. \(y = {\rm{\;}} – {x^2} – 2x + 1\). D. \(y = {\rm{\;}} – {x^2} – 2x + 3\).
Phần II: Tự luận (4 điểm)
Câu 1: Khi quả bóng được đá lên, nó sẽ đạt độ cao nào đó rồi rơi xuống đất. Biết rằng quỹ đạo của quả là một cung parabol trong mặt phẳng với hệ tọa độ Oth, trong đó \(t\) là thời gian kể từ khi quả bóng được đá lên; \(h\) là độ cao của quả bóng. Giả thiết rằng quả bóng được đá lên từ độ cao 1,2m. Sau đó 1 giây, nó đạt độ cao 8,5m và 2 giây sau khi đá lên, nó ở độ cao 6m. Hãy tìm hàm số bậc hai biểu thị độ cao \(h\) theo thời gian \(t\) và có phần đồ thị trùng với quỹ đạo của quả bóng trong tình huống trên.
Câu 2: Cho hình bình hành ABCD và hai điểm \(E,{\mkern 1mu} F\) được xác định bởi các hệ thức sau: \(\;2\overrightarrow {CE} {\rm{ \;}} + \overrightarrow {EB} {\rm{ \;}} = \vec 0{\mkern 1mu} \), \({\mkern 1mu} 3{\mkern 1mu} \overrightarrow {DF} {\rm{ \;}} + \overrightarrow {BD} {\mkern 1mu} {\mkern 1mu} = \vec 0.\)
a) Chứng minh A, E, F thẳng hàng.
b) M là điểm thỏa mãn \(2\;\overrightarrow {AM} {\rm{ \;}} = 3\;\overrightarrow {AF} \). Chứng minh \(M\) là trung điểm CD
Câu 3: Cho hàm số \(f\left( x \right) = a{x^2} + bx + c\) với a, b, c là các hệ số, \(\left( {a > 0} \right)\). Biết rằng \(f(x)\) đồng biến trên khoảng \(\left( { – 2; + \infty } \right)\), hãy tìm giá trị lớn nhất của biểu thức \(P = \frac{{6{a^2}}}{{5{a^2} + 2ab + {b^2}}}\).
—– HẾT —–