Hướng dẫn giải Luyện tập 1 Bài 4. Nhị thức Newton (trang 32, 33, 34) – Chuyên đề học tập Toán 10 Kết nối tri thức. Gợi ý: Dựa vào hàng tương ứng của tam giác Pascal.
Câu hỏi/Đề bài:
a) Sử dụng tam giác Pascal viết khai triển của \({(a + b)^7}\)
b) Sử dụng tam giác Pascal viết khai triển của \({(2x – 1)^4}\)
Hướng dẫn:
Dựa vào hàng tương ứng của tam giác Pascal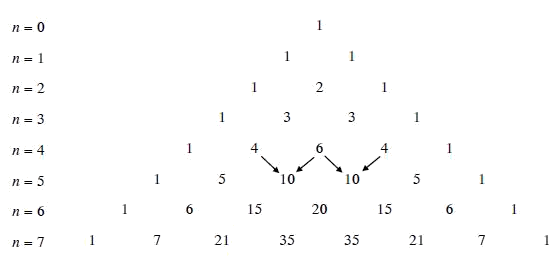
b) Viết khai triển của \({(a + b)^4}\)rồi thay \(a = 2x,b = – 1\) vào khai triển nhận được.
Lời giải:
a) Khai triển của \({(a + b)^7}\) có dạng
\({(a + b)^7} = {a^7} + ?{a^6}b + ?{a^5}{b^2} + ?{a^4}{b^3} + ?{a^3}{b^4} + ?{a^2}{b^5} + ?a{b^6} + ?{b^7}\)
Các hệ số trong khai triển này là các hệ số ở hàng 7 của tam giác Pascal. Do đó ta có ngay
\({(a + b)^7} = {a^7} + 7{a^6}b + 21{a^5}{b^2} + 35{a^4}{b^3} + 35{a^3}{b^4} + 21{a^2}{b^5} + 7a{b^6} + {b^7}\)
b) Ta viết khai triển của \({(a + b)^4}\)rồi thay \(a = 2x,b = – 1\) vào khai triển nhận được.
Dựa vào hàng 4 của tam giác Pascal, ta có
\({(a + b)^4} = {a^4} + 4{a^3}b + 6{a^2}{b^2} + 4a{b^3} + {b^4}\)
Với \(a = 2x,b = – 1\) ta được:
\(\begin{array}{l}{(2x – 1)^4} = {\left( {2x} \right)^4} + 4.{\left( {2x} \right)^3}\left( { – 1} \right) + 6.{\left( {2x} \right)^2}{\left( { – 1} \right)^2} + 4.2x.{\left( { – 1} \right)^3} + {\left( { – 1} \right)^4}\\ = 16{x^4} – 32{x^3} + 24{x^2} – 8x + 1\end{array}\)