Hướng dẫn giải Hoạt động 4 Bài 1. Elip (trang 41) – Chuyên đề học tập Toán 10 Cánh diều. Hướng dẫn: Trong mặt phẳng tọa độ \(Oxy\), ta xét Elip \(\left( E \right)\) có phương trình chính tắc là.
Câu hỏi/Đề bài:
Quan sát elip \(\left( E \right)\) phương trình chính tắc là: \(\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1\) trong đó \(a > b > 0\) và hình chữ nhật cơ sở PQRS của \(\left( E \right)\)(Hình 5)
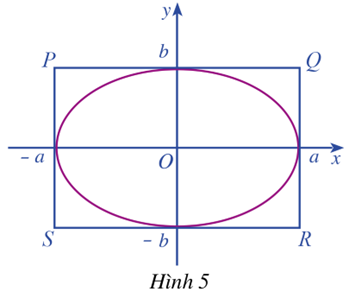
a) Tính tỉ số giữa hai cạnh \(\frac{{QR}}{{PQ}}\) của hình chữ nhật \(PQRS\)
b) Tỉ số \(\frac{{QR}}{{PQ}}\) phản ánh đặc điểm gì của \(\left( E \right)\) về hình dạng?
Hướng dẫn:
Trong mặt phẳng tọa độ \(Oxy\), ta xét Elip \(\left( E \right)\) có phương trình chính tắc là: \(\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1\), trong đó \(a > b > 0\) . Khi đó ta có hình chữ nhật cơ sở có bốn đỉnh là \(P\left( { – a;b} \right),Q\left( {a;b} \right),R\left( {a; – b} \right),S\left( { – a; – b} \right)\)
Lời giải:
a) Ta có hình chữ nhật cơ sở có bốn đỉnh là \(P\left( { – a;b} \right),Q\left( {a;b} \right),R\left( {a; – b} \right),S\left( { – a; – b} \right)\)
Suy ra \(QR = 2b,PQ = 2a \Rightarrow \frac{{QR}}{{PQ}} = \frac{{2b}}{{2a}} = \frac{b}{a}\)
b) Ta có \(\frac{{QR}}{{PQ}} = \frac{b}{a}\), vì \(0 < b < a\) nên \(0 < \frac{b}{a} < 1\). Tỉ số \(\frac{b}{a}\) phản ánh cụ thể hình dạng của \(\left( E \right)\) như sau:
+ Nếu tỉ số \(\frac{b}{a}\) càng bé thì hình chữ nhật cơ sở càng “dẹt”, do đó \(\left( E \right)\) càng “gầy”
+ Nếu tỉ số \(\frac{b}{a}\) càng lớn thì b càng gần a và hình chữ nhật cơ sở càng gần với hình vuông, do đó \(\left( E \right)\) càng “béo”