Bài 1 trang 37 Chuyên đề học tập Toán 10 – Cánh diều: Khai triển biểu thức: a) (2x + y) ^6 b) (x – 3y) ^6 c) (x – 1) ^n d) (x + 2) ^n e) (x + y) ^2n f) (x – y) ^2n

Đề bài/câu hỏi:

Khai triển biểu thức:

a) \({(2x + y)^6}\)

b) \({(x – 3y)^6}\)

c) \({(x – 1)^n}\)

d) \({(x + 2)^n}\)

e) \({(x + y)^{2n}}\)

f) \({(x – y)^{2n}}\)

Hướng dẫn:

Sử dụng công thức nhị thức Newton

\({(a + b)^n} = C_n^0{a^n} + C_n^1{a^{n – 1}}b + … + C_n^{n – 1}a{b^{n – 1}} + C_n^n{b^n}\)

hoặc tam giác Pascal

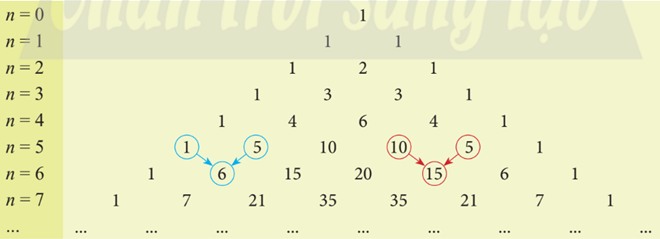
Lời giải:

a) Sử dụng tam giác Pascal, ta có:

\(\begin{array}{l}{(2x + y)^6} = {\left( {2x} \right)^6} + 6{\left( {2x} \right)^5}.y + 15{\left( {2x} \right)^4}.{y^2} + 20{\left( {2x} \right)^3}.{y^3} + 15{\left( {2x} \right)^2}.{y^4} + 6\left( {2x} \right).{y^5} + {y^6}\\ = 64{x^6} + 192{x^5}y + 240{x^4}{y^2} + 160{x^3}{y^3} + 60{x^2}{y^4} + 12x{y^5} + {y^6}\end{array}\)

b) Sử dụng tam giác Pascal, ta có:

\(\begin{array}{l}{(x – 3y)^6} = {x^6} + 6{x^5}.\left( { – 2y} \right) + 15{x^4}.{\left( { – 3y} \right)^2} + 20{x^3}.{\left( { – 3y} \right)^3} + 15{x^2}.{\left( { – 3y} \right)^4} + 6x.{\left( { – 3y} \right)^5} + {\left( { – 3y} \right)^6}\\ = {x^6} – 12{x^5}y + 135{x^4}{y^2} – 540{x^3}{y^3} + 1215{x^2}{y^4} – 1458x{y^5} + 729{y^6}\end{array}\)c) Sử dụng công thức nhị thức Newton

\({(x – 1)^n} = C_n^0{x^n} + C_n^1{x^{n – 1}}{\left( { – 1} \right)^1} + … + C_n^{n – 1}x{\left( { – 1} \right)^{n – 1}} + C_n^n{\left( { – 1} \right)^n}\)

d) Sử dụng công thức nhị thức Newton

\({(x + 2)^n} = C_n^0{x^n} + C_n^1{x^{n – 1}}{.2^1} + … + C_n^{n – 1}x{.2^{n – 1}} + C_n^n{.2^n}\)

e) Sử dụng công thức nhị thức Newton

\({(x + y)^{2n}} = C_{2n}^0{x^{2n}} + C_{2n}^1{x^{2n – 1}}{y^1} + … + C_{2n}^{2n – 1}x{y^{2n – 1}} + C_{2n}^{2n}{y^{2n}}\)

f) Sử dụng công thức nhị thức Newton

\({(x – y)^{2n}} = C_{2n}^0{x^{2n}} + C_{2n}^1{x^{2n – 1}}{\left( { – y} \right)^1} + … + C_{2n}^{2n – 1}x{\left( { – y} \right)^{2n – 1}} + C_{2n}^{2n}{\left( { – y} \right)^{2n}}\)